2019学年高二数学下学期第五次月考试题 文 新人教版 7页

‎2019届高二年级第五次月考数学（文）试卷 一、选择题(本大题共12小题，每小题5分，共60分)‎ ‎1．如图,函数f(x)在A,B两点间的平均变化率是( )‎ A．1 B．‎ C．2 D．‎ ‎2.已知y＝，则y′＝ (　　)‎ A. B．－ C. D．0‎ ‎3．函数f(x)＝(x＋2a)(x－a)2的导数为(　　)‎ A．2(x2－a2) B．2(x2＋a2) C．3(x2－a2) D．3(x2＋a2)‎ ‎4已知函数f(x)的导数为，且满足关系式，则的值等于(　　)‎ A．－2 B．2 C．－ D. ‎5.以下四个命题中：‎ ‎①在回归分析中，可用相关指数R2的值判断拟合的效果，R2越大，模型的拟合效果越好；‎ ‎②两个随机变量的线性相关性越强，相关系数的绝对值越接近1；‎ ‎③若数据x1，x2，x3，…，xn的方差为1，则2x1,2x2,2x3，…，2xn的方差为2；‎ 其中真命题的个数为(　　)‎ A．3 B．2 C．1 D．0‎ ‎6.设曲线在点（1,0）处的切线方程为y=2x-2，则a=（ ）‎ A. ‎0 B.1 C.2 D.3‎ ‎7.已知曲线与曲线在交点处有公切线，则实数的值为( )‎ A.0 B.1 C.-1 D.2 ‎ - 7 -‎ ‎8.已知函数是奇函数，当时，，则曲线在处的切线方程为( )‎ A． B．‎ C． D．‎ ‎9.若函数f(x)=2x3-9x2+12x-a恰好有两个不同的零点,则a可能的值为(　　)‎ A.4 B.6 C.7 D.8‎ ‎10.．设154；‎ ‎∴c(54,+），此即为参数c的取值范围。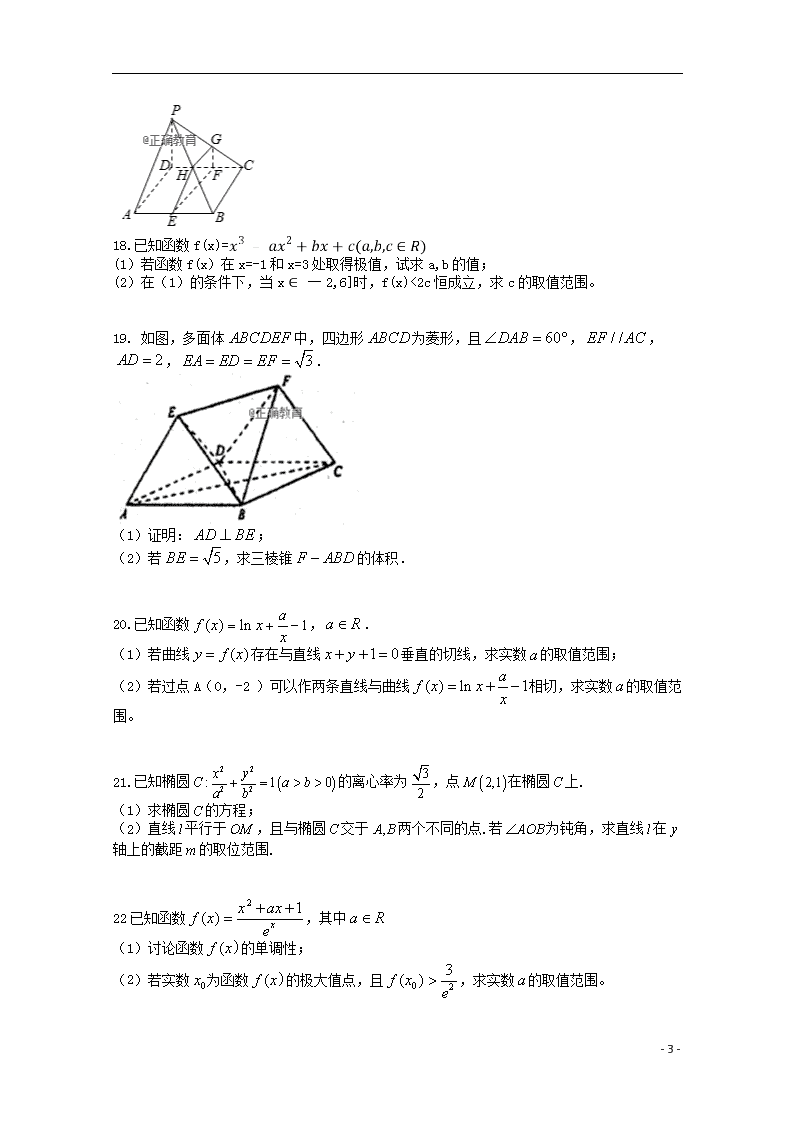‎ ‎19.解：（1）如图，取的中点，连接，，‎ 因为，所以，‎ 因为四边形为菱形，所以，‎ 因为，所以．‎ 因为，所以平面，‎ 因为平面，所以．　‎ ‎（2）在中，，，所以．‎ 因为是等边三角形，所以，．‎ 因为，所以，所以．‎ 又因为，，所以平面，‎ 因为，，‎ 所以．‎ ‎20（1）（2）‎ - 7 -‎ ‎20. （1）依题意有 解得 故椭圆的方程为. ‎ ‎（2）由直线平行于，得直线的斜率，‎ 又在轴上的截距为，所以的方程为.‎ 由得.‎ 因为直线与椭圆交于两个不同的点，所以，‎ 解得. ‎ 设，又为钝角等价于且，‎ 则，‎ 将代入上式，‎ 化简整理得，即，‎ 故的取值范围是.‎ ‎21、‎ - 7 -‎ ‎22、（1）‎ - 7 -‎ - 7 -‎