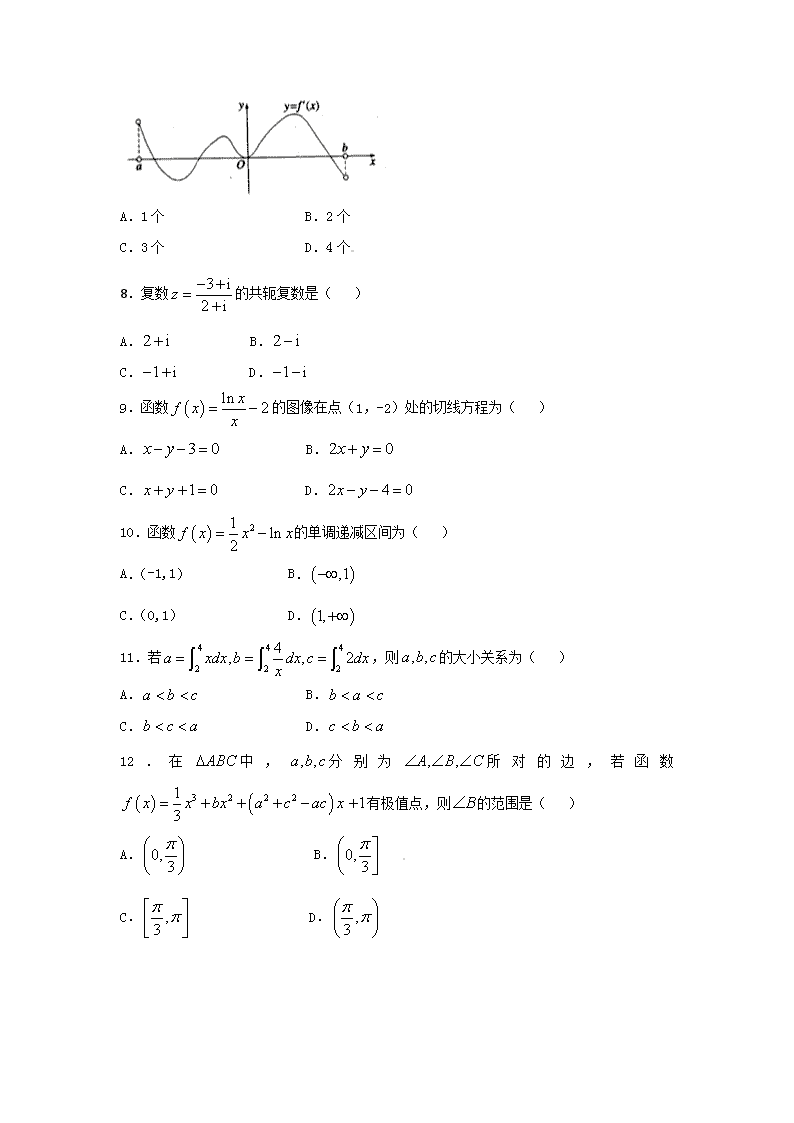- 1.33 MB
- 2021-04-22 发布
2017-2018 学年高二第二学期 3 月月考理科数学试题
班级 姓名 学号
一、单选题(每题 5 分,共 60 分)
1.设 则 等于( )
A. B.
C. D.不存在
2.抛物线 在点 的切线的倾斜角是( )
A.30° B.45°
C.60° D.90°
3.函数 在 上的最小值 为( )
A. 2 B. -2 C. 0 D. -4
4.设函数 的导函数为 ,且 ,则 等于( )
A.0 B.-4 【来源:全,品…中&高*考+网】
C.-2 D.2
5.设 是虚数单位,如果复数 的实部与虚部互为相反数,那么实数 的值为( )
A. B.
C.3 D.
6.已知点 A(l,2)在函数 f(x)=ax3 的图象上,则过点 A 的曲线 C:y=f(x)的切线方程
是( )
A. 6x﹣y﹣4=0 B. x﹣4y+7=0
C. 6x﹣y﹣4=0 或 x﹣4y+7=0 D. 6x﹣y﹣4=0 或 3x﹣2y+1=0
7.函数 的定义域为开区间 ,导函数 在 内的图像如下图所示,则函
数 在开区间 内有极大值点( )
( ) ( )
( )
2 0 1 ,
2 1 2 ,
x x
f x
x x
≤ <= − ≤ ≤
( )2
0
f x dx∫
3
4
4
5
5
6
2y x= 1 1,2 4M
( )f x ( )f x′ ( ) ( )2 2 1f x x x f ′= + ( )0f ′
i i
2 i
a −
+ a
1
3
1
3
−
3−
( )f x ( ),a b ( )f x′ ( ),a b
( )f x ( ),a b
A.1 个 B.2 个
C.3 个 D.4 个
8.复数 的共轭复数是( )
A. B.
C. D.
9.函数 的图像在点(1,-2)处的切线方程为( )
A. B.
C. D.
10.函数 的单调递减区间为( )
A.(-1,1) B.
C.(0,1) D.
11.若 ,则 的大小关系为( )
A. B.
C. D.
12 . 在 中 , 分 别 为 所 对 的 边 , 若 函 数
有极值点,则 的范围是( )
A. B.
C. D.
3 i
2 iz
− += +
2 i+ 2 i−
1 i− + 1 i− −
( ) ln 2xf x x
= −
3 0x y− − = 2 0x y+ =
1 0x y+ + = 2 4 0x y− − =
( ) 21 ln2f x x x= −
( ),1−∞
( )1,+∞
4 4 4
2 2 2
4, , 2a xdx b dx c dxx
= = =∫ ∫ ∫ , ,a b c
a b c< < b a c< <
b c a< < c b a< <
ABC∆ , ,a b c , ,A B C∠ ∠ ∠
( ) ( )3 2 2 21
3f x x bx a c ac x= + + + − 1+ B∠
0, 3
π
0, 3
π
,3
π π
,3
π π
二、填空题(每题 5 分,共 20 分)
13.
14.设 若 ,则 _____________.
15.已知函数 , ,对于任意 、 .不等式 恒成
立,则正数 的最小值为__________.
16.若复数 ( 是虚数单位)是纯虚数,则实数 的值为__________..【来源:全,品…中&高*考+网】
三. 解答题
17(10 分)已知 ,且 在 处取得极值.
(Ⅰ)求 的值;
(Ⅱ)求 在 上的最值.
18(12 分).已知函数 . (1)求函数 的最小值;
(2)若 对任意的 恒成立,求实数 t 的取值范围.
( )1
2
1
1 sinx x dx
−
− + =∫
2
0
lg , 0,
( )
3 , 0,a
x x
f x
x t dt x
>= + ≤ ∫ ( (1)) 1f f = a =
( ) ( )2
0
2
x
f x t at dt= − −∫ ( )f x 1x = −
a
( )f x [ ]2,3−
19(12 分).已知函数 ,
(1)若曲线 在点 处的切线方程为 ,求 ;
(2)求函数 的极值.
20(12 分).已知函数 ,其中 ,且 在 处取得
极值.
(1)求 的值;
(2)求函数 的单调区间.
21(12 分).已知函数 (1)求 的单调区间;
(2)当 时,若 恒成立,求 的取值范围.
22(12 分).已知 f(x)=ex(x3+mx2-2x+2).
(1)假 设 m=-2,求 f(x)的极大值与极小值;
(2)是否存在实数 m,使 f(x)在[-2,-1]上单调递增?如果存在,求 m 的取值范围;如果不存在,
请说明理由.
参考答案
( ) 2 ln 5af x x xx
= + − − a R∈ ( )f x 2x =
a
( )f x
1.A
【解析】
试题分析:因为函数 有极大值和极小值,所以 有
两个不同的实数根,而 解得
或 .
考点:本小题主要考查导数的计算和应用.
点评:解决本 小题的关键在于将存在极值问题转化为二次函数根的存在问题,解决问题时
要注意转化思想的灵活应用.
2.C
【解析】
试题分析:复数 的模长为 ,所以 ,
故选 C
考点:复数模长计算.
3.A
【解析】若函数 是 R 上的单调函数,只需 恒成立,
即△=4−12m⩽0,∴m⩾ .【来源:全,品…中&高*考+网】
故选 A.
点睛:本题考查导数和函数的单调性的关系;已知函数在某区间上单调时,往往转化为导函
数恒为正或恒为负,如: 为 上的单调递增函数,所以 恒成立,而不要错
误认为“ 恒成立”,若只是求函数的增区间可直接令 即可.
4.A
【解析】 ,因为函数 在 内存在单调递减区间,
在 内成立, ,所以实数 的取值范围是 ,故选
A.
【方法点晴】本题主要考查“分离常数”在解题中的应用及利用单调性求参数的范围,属于中
档题. 利用单调性求参数的范围的常见方法:① 视参数为已知数,依据函数的图象或单调
1)6()( 23 ++++= xaaxxxf ( ) 0f x′ =
2 2( ) 3 2 ( 6) 0, (2 ) 12( 6) 0,f x x ax a a a′ = + + + = ∴∆ = − + >
3−a
yixz += 22|| yxz += 5)4(3|z|43 22 =−+=⇒−= iz
3 2 1y x x mx= + + + 2' 3 2 0y x x m= + +
1
3
( )f x R ( ) 0f x′ ≥
( ) 0f x′ > ( ) 0f x′ >
( )' 1af x x
= − ( )f x 2,x e e ∈ ( )' 0f x∴ ≤
( )2,x e e∈ 21 0,a a x ex
∴ − ≤ ∴ ≤ < a ( )2,e−∞
性定义,确定函数的单调区间,与已知单调区间比较求参数需注意若函数在区间 上是
单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式
或 恒成立问题求参数范围,本题是利用方法 ① 求解的.
5.B
【解析】因为函数 存在两个极值点,则 = = =0 有二不
等根;即函数 与 的图像有 2 个交点;k ,则 ,所以 ;
= ,解得 ;即当 时, 与 相切,此时有 1 个交点;而
与 的图像有 2 个交点,所以 ;即实数 的取值范围是 .故选 B.
6.A
【解析】由 知 , ,构造函数
,则 ,易知 在 R 上单调递增,且 任
一点处斜率比 相应点的斜率大,又 ,知 0,故作出 及
的草图,如下:
通过图像分析 的解集为 ,故选 A
点睛:构造函数 ,通过分析 与 的图像关系,作出图像,
是解决本题的关键.
7.D
【解析】
试题分析:因 为 ,故选 D.
考点:复数的运算.
8.C
[ ],a b
( )' 0f x ≤
( )' 0f x ≥
( )f x ( )'f x ln 1— 1x ax+ − lnx ax−
lny x= y ax=
0
1y ax
= =′ = 0
1 0x a
= > 0a >
0
1 1y aa
= × = 1ln a
1
ea = 1
ea = lny x= y ax=
lny x= y ax= 10 ea< < a 10, e
( ) ( )1f x f x> − ′ ( ) ( ) 1f x f x+ ′ > ( ) ( )' 0x x xe f x e f x e+ > >
( ) ( )F xx e f x= ( )( ) ( )' 'x xe f x e> ( )F x ( ) ( )F xx e f x=
y xe= ( )0 0f = ( )F 0 = ( )xy e f x=
1xy e= −
( ) 1x xe f x e> − ( )0,+∞
( ) ( )F xx e f x= ( )F x ( )xy e f x=
2
4 3i i(4 3i) 3 4ii iz
− −= = = − −
【解析】
试 题 分 析 : 复 数 , 所 以 在 复 平 面 内 对 应 的 点 为
在 第 四 象 限 内 , 所 以 A 错 误 ; 其 共 轭 复 数 为 , 所 以 B 错 误 ; 当
为 纯 虚 数 时 , , 所 以 C 正 确 ;
,所以 D 错误,故选 C.
考点:复数的运算与复数的有关概念.
9.A
【解析】
试题分析:把已知的等式变形,利用复数代数形式的乘除运算化简得答案.
解:由 z(1+i)=3+i,得 ,
∴ ,
故选:A.
考点:复数代数形式的乘除运算.
10.C
【解析】试题分析:∵ ,∴ ,则 ,∴曲线 在点
处的切线方程为 即 ,令 ,解得 ,∴曲线 在点
处 的切线与 y 轴交点的纵坐标是 9,故选 C.
考点:利用导数研究曲线上某点切线方程.
11.A
【解析】
试题分析: ,选 A.
考点:复数概念
【名师点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四
则 运 算 , 要 切 实 掌 握 其 运 算 技 巧 和 常 规 思 路 , 如
( )
( )( )
3 1 1
1 1 1 1 2
i ii i iz i i i i
− +− −= = = =− − − +
1 1,2 2
−
1
2 2
iz = +
1
1 1
2 2z z b b i = + = + −
1 10,2 2b b+ = ∴ = −
2 21 1 2
2 2 2z = + =
1 1 1 | 1|z | | | | 11 1 1 |1 |
z i i ii zz i i i
+ − − −= ⇒ = ⇒ = = =− + + +
. 其次要熟悉复数相关基本概念,
如复数 的实部为 、虚部为 、模为 、共轭为
12.B.
【解析】 ,所以虚部为 ,应选 B
13.B
【解析】本题考查导数的运算,利用导数求函数的单调区间.【来源:全,品…中&高*考+网】
函数 的定义域是 ,解不等式 得 ,
解得 所以函数 的减区间是
14.B
【解析】略
15.
【解析】解:求 导数
16. 或 .
【 解 析 】 试 题 分 析 : , , 故 所 求 的 切 线 的 斜 率 为
,
故所求的切线的方程为 ,即 或 .
考点:本题考查利用导数求函数图象的切线问题,属于中等题.
视频
17.[ ,+∞)
【解析】
试题分析:求出两个函数的导函数,设出两切点,由斜率相等列方程,再由方程有根转化为
两函数图象有交点,求得 a 的范围.
解:由 y=ax2(a>0),得 y′=2ax,
( )( ) ( ) ( ) ,( , , . )+ + = − + + ∈a bi c di ac bd ad bc i a b c d R
( , )+ ∈a bi a b R a b 2 2+a b .−a bi
23( ) 3 41
i ii
− = − −+ 4−
lny x x= (0, ),+∞ ln 1y x′ = + ln 1 0y x′ = + < ln 1x < −
10 ,x e
< < lny x x= 1(0, ).e
(-2,0);(- -2),(0,+ )∞ ∞
2 2( ) '( ) 2
( 2),
'( ) 0, -2 0
'( ) 0, -2 0
当 则
当 则x< 或
x x x
x
f x e x f x e x e x
e x x
f x x
f x x
= ⋅ ∴ = ⋅ + ×
= +
< < <
> >
5 2y x= − − 5 2 0x y+ + =
5 3xy e= − + 5 xy e∴ ′ = −
05 5k e= − = −
( )2 5y x− − = − 5 2y x= − − 5 2 0x y+ + =
由 y=ex,得 y′=ex,
曲线 C1:y=ax2(a>0)与曲线 C2:y=ex 存在公共切线,
设公切线与曲线 C1 切于点(x1,ax12),与曲线 C2 切于点(x2,ex2),
则 2ax1=ex2= ,
可得 2x2=x1+2,
∴a= ,
记 f(x)= ,
则 f′(x)= ,
当 x∈(0,2)时,f′(x)<0,f(x)递减;
当 x∈(2,+∞)时,f′(x)>0,f(x)递增.
∴当 x=2 时,f(x)min= .
∴a 的范围是[ ,+∞).
故答案为:[ ,+∞).
考点:利用导数研究曲线上某点切线方程.
18.2
【解析】 时, 时, 时,
, 是 的极小值点,又 为 的极小值点, ,故答案
为 .
【方法点睛】本题主要考查利用导数判断函数的单调性以及函数的极值,属于中档题.求函
数 极值的步骤:(1) 确定函数的定义域;(2) 求导数 ;(3) 解方程 求
出函数定义域内的所有根;(4) 列表检查 在 的根 左右两侧值的符号,如
果左正右负(左增右减),那么 在 处取极大值,如果左负右正(左减右增),那么
( ) 2' 3 12, 2f x x x= − ∴ < − ( )' 0, 2 2f x x> − < < ( )' 0, 2f x x
( )' 0f x > 2x∴ = ( )f x 0x ( )f x 0 2x∴ =
2
( )f x ( )f x′ ( ) 0,f x′ =
( )f x′ ( ) 0f x′ = 0x
( )f x 0x ( )f x
在 处取极小值.
19.(Ⅰ) (Ⅱ)
【解析】试题分析: (Ⅰ)先求出函数的导函数,将 代入可得在此切点处的斜率,再由
曲线方程可求出切点坐标,利用点斜式式写出切线方程; (Ⅱ)求出 的导函数函数,令
为 ,再求 的导函数,去判断 的单调性,再进一步判断 的单调性,可求
出 的最小值,将恒成立问题转为关于 的不等式即可.注意对 的分类讨论.
试题解析:(Ⅰ)当 时,有 ,
则 .
又因为 ,
∴曲线 在点 处的切线方程为 ,即 .
(Ⅱ)因为 ,令
有 ( )且函数 在 上单调递增
当 时 , 有 , 此 时 函 数 在 上 单 调 递 增 , 则
(ⅰ)若 即 时,有函数 在 上单调递增,
则 恒成立;
(ⅱ)若 即 时,则在 存在 ,
此时函数 在 上单调递减, 上单调递增且 ,
所以不等式不可能恒成立,故不符合题意;
当 时,有 ,则在 存在 ,此时 上单调
递减, 上单调递增所以函数 在 上先减后增.
又 ,则函数 在 上先减后增且 .
所以不等式不可能恒成立,故不符合题意;
0x
2y x= 1
2a ≥
0x =
( )f x
( )g x ( )g x ( )g x ( )f x
( )f x a a
1a = ( ) ( )22 4) 2xf x x e x= − + +(
( ) ( )' 2 2) 2 4 ' 0 2 4 2xf x x e x f= − + + ⇒ = − + =(
( )0 4 4 0f = − + =
( )y f x= ( )( )0, 0P f ( )0 2 0y x− = − 2y x=
( ) ( )' 2 2) 2 2xf x x e a x= − + +( ( ) ( ) ( )' 2 2) 2 2xg x f x x e a x= = − + +(
( )' 2 2xg x x e a= ⋅ + 0x ≥ ( )'y g x= [ )0,x∈ +∞
2 0a ≥ ( )' 0g x ≥ ( )'y f x= [ )0,x∈ +∞
( ) ( )' ' 0 4 2f x f a≥ = −
4 2 0a − ≥ 1
2a ≥ ( )y f x= [ )0,x∈ +∞
( ) ( )min 0 4 4f x f a= = −
4 2 0a − < 10 2a≤ < [ )0,x∈ +∞ ( )0' 0f x =
( )y f x= ( )00,x x∈ ( )0 ,x x∈ +∞ ( )0 4 4f a= −
2 0a < ( )' 0 2 0g a= < [ )0,x∈ +∞ ( )1' 0g x = ( )10,x x∈
( )1,x x∈ +∞ ( )'y f x= [ )0,x∈ +∞
( )' 0 2 4 0f a= − + < ( )y f x= [ )0,x∈ +∞ ( )0 4 4f a= −
综上所述,实数 的取值范围为 .
20.(1) , ,(2) .
【解析】
试题分析:(1)根据导数几何意义,所以 .因为 ,所以 .因为
过点 ,所以 ,(2)由题意得:不等式 恒成立,恒成立
问题一般转化为最值问题.一是分类讨论求函数 最小值,二是变量分离为
恒成立,求函数 最小值.两种方法都是 ,然后
对实数 a 进行讨论,当 时, ,所以 .当 时,由 得
,不论 还是 , 都是先减后增,即 的最小值为 ,所
以 .
试题解析:解
(1) , 2 分
因为曲线 C 在点(0,1)处的切线为 L: ,
所以 且 . 4 分
解得 , -5 分
(2)法 1:
对于任意实数 a,曲线 C 总在直线的 的上方,等价于
∀x, ,都有 ,
即∀x, R, 恒成立, 6 分
令 , 7 分
①若 a=0,则 ,
所以实数 b 的取值范围是 ; 8 分
②若 , ,
a 1
2a ≥
1m = 2a = 1b <
2)0( =′f eaxy a′ = 2a =
2y x m= + (0,1) 1m = e 0ax ax b− − >
( ) eaxg x ax b= − −
eaxb ax< − axexg ax −=)( ( ) (e 1)axg x a′ = −
0=a ( ) 1g x b= − 1b < 0≠a '( ) 0g x =
0x = 0>a 0 +
a∈ e 0ax ax b− − >
( ) eaxg x ax b= − −
( ) 1g x b= −
1b <
0a ≠ ( ) (e 1)axg x a′ = −
由 得 , 9 分
的情况如下:
0
0 +
极小值
11 分
所以 的最小值为 , 12 分
所以实数 b 的取值范围是 ;
综上,实数 b 的取值范围是 . 13 分
法 2:对于任意实数 a,曲线 C 总在直线的 的上方,等价于
∀x, ,都有 ,即
∀x, R, 恒成立, 6 分
令 ,则等价于∀ , 恒成立,
令 ,则 , 7 分
由 得 , 9 分
的情况如下:
0
0 +
极小值
【来源:全,品…中&高*考+网】
-11 分
所以 的最小值为 , 12 分
实数 b 的取值范围是 . 13 分
考点:利用导数求切线、最值.
'( ) 0g x = 0x =
'( ), ( )g x g x
x 0∞(- , ) ∞(0, + )
'( )g x −
( )g x
( )g x (0) 1g b= −
1b <
1b <
y ax b= +
a R∈ eax ax b> +
a ∈ eaxb ax< −
t ax= t ∈R etb t< −
( ) etg t t= − ( ) e 1tg t′ = −
'( ) 0g t = 0t =
'( ), ( )g t g t
t 0∞(- , ) ∞(0, + )
'( )g t −
( )g t
( ) etg t t= − (0) 1g =
1b <
21.(1) , .
(2) 在 和 上是单调递增的;在 和 上是单调递减的.
(3)(1) 且 时
(2) 或 时,
【解析】(Ⅰ)因为 ,
又 和 为 的极值点,所以 ,
因此 解该方程组得 , .
(Ⅱ)因为 , ,所以 ,
令 ,解得 , , .
因为当 时, ;
当 时, .
所以 在 和 上是单调递增的;在 和 上是单调递减的.
(Ⅲ)由(Ⅰ)可知 ,
故 ,令 ,则 .
令 ,得 ,因为 时, ,
所以 在 上单调递减.故 时, ;
因为 时, ,所以 在 上单调递增.
故 时, .
所以对任意 ,恒有 ,又 时, ,
因此 且 时 ,
或 时 ,
所以, (1) 且 时
1
3a = − 1b = −
( )f x ( )2,0− ( )1,+∞ ( ), 2−∞ − ( )0,1
0x ≠ 1x ≠ ( ) ( )f x g x>
1x = 0x = ( ) ( )f x g x=
( ) ( )1 2 2e 2 3 2xf x x x ax bx−′ = + + + ( ) ( )1e 2 3 2xx x x ax b−= + + +
2x = − 1x = ( )f x ( ) ( )2 1 0f f′ ′− = =
6 2 0,{ 3 3 2 0,
a b
a b
− + =
+ + =
1
3a = − 1b = −
1
3a = − 1b = − ( ) ( )( )12 e 1xf x x x −′ = + −
( ) 0f x′ = 1 2x = − 2 0x = 3 1x =
( ), 2x∈ −∞ − ( )0,1∪ ( ) 0f x′ <
( ) ( )2,0 1,x∈ − ∪ +∞ ( ) 0f x′ >
( )f x ( )2,0− ( )1,+∞ ( ), 2−∞ − ( )0,1
( ) 2 1 3 21e 3
xf x x x x−= − −
( ) ( ) ( )2 1 3 2 1e ex xf x g x x x x x− −− = − = − ( ) 1exh x x−= − ( ) 1e 1xh x −=′ −
( ) 0h x′ = 1x = ( ),1x∈ −∞ ( ) 0h x′ <
( )h x ( ),1x∈ −∞ ( ),1x∈ −∞ ( ) ( )1 0h x h> =
( )1,x∈ +∞ ( ) 0h x′ > ( )h x ( )1,x∈ +∞
( )1,x∈ +∞ ( ) ( )1 0h x h> =
( ) ( ),1 1,x∈ −∞ ∪ +∞ ( ) 0h x > 0x ≠ 2 0x >
0x ≠ 1x ≠ ( ) ( ) 0f x g x− >
1x = 0x = ( ) ( ) 0f x g x− =
0x ≠ 1x ≠ ( ) ( )f x g x>
(2) 或 时,
【注:】按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人
所接受
(Ⅲ)由(Ⅰ)可知 ,
故 ,令 ,则 .
令 ,得 ,因为 时, ,
所以 在 上单调递减.故 时, ;
因为 时, ,所以 在 上单调递增.
故 时, .
所以对任意 ,恒有 ,又 ,因此 ,
故对任意 ,恒有
视频
1x = 0x = ( ) ( )f x g x=
( ) 2 1 3 21e 3
xf x x x x−= − −
( ) ( ) ( )2 1 3 2 1e ex xf x g x x x x x− −− = − = − ( ) 1exh x x−= − ( ) 1e 1xh x −=′ −
( ) 0h x′ = 1x = ( ],1x∈ −∞ ( ) 0h x′ ≤
( )h x ( ],1x∈ −∞ ( ],1x∈ −∞ ( ) ( )1 0h x h≥ =
[ )1,x∈ +∞ ( ) 0h x′ ≥ ( )h x [ )1,x∈ +∞
[ )1,x∈ +∞ ( ) ( )1 0h x h≥ =
( ),x∈ −∞ +∞ ( ) 0h x ≥ 2 0x ≥ ( ) ( ) 0f x g x− ≥
( ),x∈ −∞ +∞ ( ) ( )f x g x≥