- 1.52 MB
- 2021-04-21 发布
北京京新学道临川学校第三次月考数学理科试卷
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若命题“”为假,且“”为假,则
A. 或为假 B. 真 C. 假 D. 不能判断的真假
【答案】C
【解析】
试题分析:命题“”为假,说明与中至少有一个是假命题,“”为假说明为真命题,所以为假命题.
考点:本小题主要考查了由复合命题的真假判断命题的真假.
点评:解决此类问题的关键是掌握复合命题的真值表并能熟练应用.
2.如果椭圆上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离
A. 6 B. 10 C. 12 D. 14
【答案】D
【解析】
由椭圆知椭圆长轴长为设椭圆另一个焦点为,根据椭圆定义得:故选D
3.根据一组数据(24,25),(26,25),(26,26),(26,27),(28,27),用最小二乘法建立的回归直线方程为=kx+13,则k=( )
A. 2 B. 4 C. D.
【答案】C
【解析】
【分析】
求得样本中心点,代入回归直线方程,由此求得的值.
【详解】依题意,所以样本中心点为,代入回归直线方程得.
故选:C.
【点睛】本小题主要考查回归直线方程过样本中心点,属于基础题.
4. 设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a= ( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】
D
试题分析:根据导数的几何意义,即f′(x0)表示曲线f(x)在x=x0处的切线斜率,再代入计算.
解:,
∴y′(0)=a﹣1=2,
∴a=3.
故答案选D.
考点:利用导数研究曲线上某点切线方程.
5.定积分的值为( )
A. B. C. D.
【答案】C
【解析】
试题分析:=.故选C.
考点:1.微积分基本定理;2.定积分的计算.
6.执行如图所示的程序框图,若,则输出的( )
A. B. C. D.
【答案】B
【解析】
分析:依次运行框图中程序后可得结果.
详解:依次运行程序框图中的程序可得:
①,满足条件,继续运行;
②,满足条件,继续运行;
③,不满足,停止运行.输出4.
故选B.
点睛:对于判断程序框图的输出结果的问题,首先要弄清程序框图的功能.对于条件结构,要根据条件进行判断,弄清程序的流向;对于循环结构,要弄清楚循环体是什么、变量的初始条件是什么和循环的终止条件是什么,要特别注意循环终止时各变量的当前值.
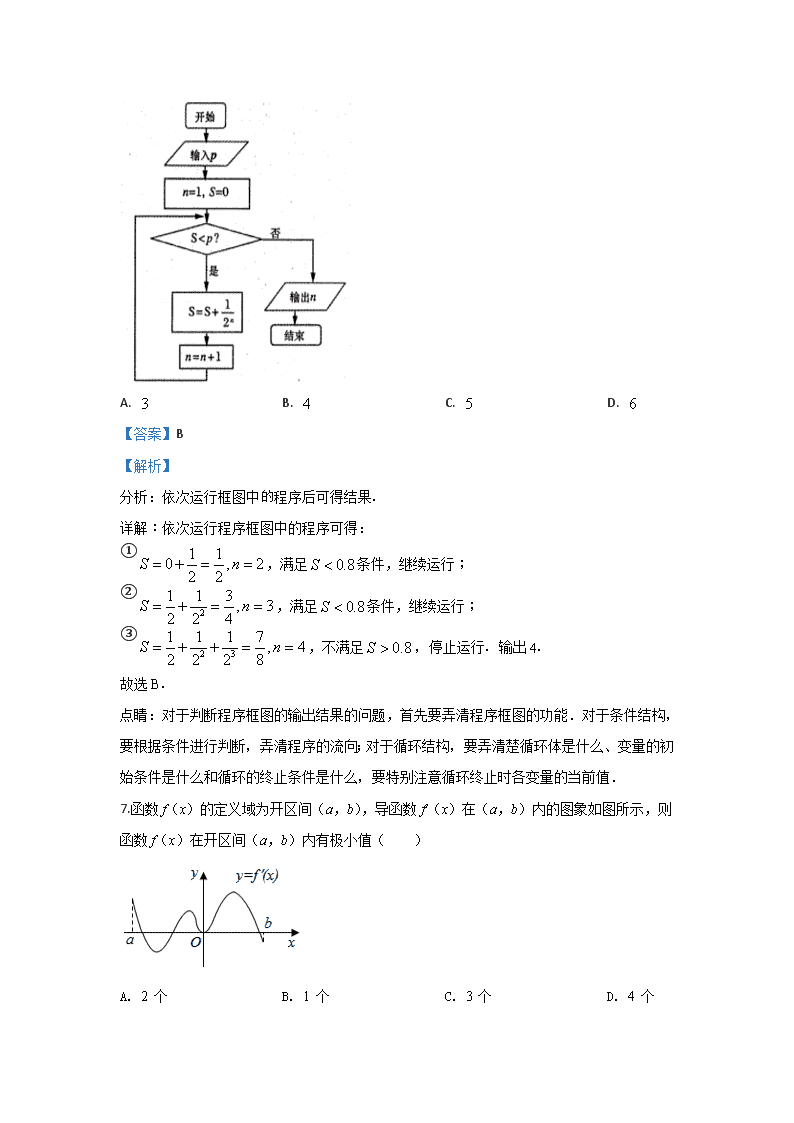
7.函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值( )
A. 2 个 B. 1 个 C. 3 个 D. 4 个
【答案】B
【解析】
【分析】
根据函数与导函数的关系以及极小值的定义,若为函数f(x)的极小值,则,且在左负右正,结合图像可得解.
【详解】根据函数与导函数的关系以及极小值的定义,
若为函数f(x)的极小值,则,且在左负右正.
结合图像可知满足条件的有1个.
故选:B
【点睛】本题考查了利用导函数图像判断函数极小值的个数,考查了学生概念理解,数形结合的能力,属于中档题.
8.若函数在区间上单调递增,则实数的取值范围是( )
A. B. C. D.
【答案】D
【解析】
【详解】试题分析:,∵函数在区间单调递增,∴在区间上恒成立.∴,而在区间上单调递减,∴.∴的取值范围是.故选D.
考点:利用导数研究函数的单调性.
9.若复数z=(x2-4)+(x+3)i(x∈R),则“z是纯虚数”是“x=2”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
【解析】
分析:先通过复数的基本概念,求出“为纯虚数”的最简形式,判断前者成立能否推出后者成立,反之后者成立能否推出前者成立,利用充要条件的定义,即可得到结论.
详解:“为纯虚数”的充要条件为,即,
因为成立推不出城,反之若成立,则成立,
所以“为纯虚数”是“”的必要不充分条件,故选B.
点睛:本题主要考查了充要条件的判定,以及复数的基本概念,其中熟记复数的基本概念即应用是解答的关键,着重考查了推理与论证能力.
10. 从装有2个红球和2个黑球的口袋内任取2个球,则恰有一个红球的概率是( )
A. B. C. D.
【答案】C
【解析】
试题分析:从装有个红球和个黑球的口袋内任取个球,共有种方法;其中恰有一个红球的方法为种,因此恰有一个红球的概率为,故选C.
考点:古典概型及其概率的计算.
11.设是上的奇函数,当时,,且,则不等式的解集是( )
A. B.
C. D.
【答案】D
【解析】
试题分析:因为所以当时,,即在上单调递增,且又因为所以如图所示,所以的解集为故选D.
考点:1、应用导数求单调性.
【思路点晴】本题主要考查的是应用导数求函数的单调性,属于难题.由是奇函数可知,图像关于原点对称,只需做出时的图像,则整个图像就可以做出来.时,在上单调递增.图像上有一点这样的大致图像就如图所示,的解集就是分布在三四象限的图像对于的x的集合.
12.已知F是双曲线的右焦点,P是C左支上一点.,当最小时,在x轴上找一点Q,使最小,最小值为( )
A. B. 10 C. D.
【答案】A
【解析】
【分析】
首先根据最小,判断出点的位置,求得点坐标,再求得关于轴对称点的坐标,即的最小值.
【详解】设双曲线左焦点的坐标为,根据双曲线的定义可知,所以最小时,最小,此时三点共线.直线的方程为,与双曲线方程联立,消去
并化简得,解得,或(舍去),所以,故.关于轴的对称点为,连接,交轴于,此时取得最小值,且最小值为.
故选:A
【点睛】本小题主要考查直线和双曲线的位置关系,考查双曲线的定义,考查双曲线中的最值问题,考查数形结合的数学思想方法,属于中档题.
二填空题:本大题共4小题,每小题5分,共20分.
13.把命题“”的否定写在横线上______________.
【答案】
【解析】
【分析】
根据特称命题是全称命题的知识填写出结果.
【详解】根据特称命题的否定是全称命题的知识可知,原命题的否定为:
.
故答案为:
【点睛】本小题主要考查特称命题否定,属于基础题.
14.复数___________.
【答案】
【解析】
【分析】
利用复数的乘方和除法运算,化简表达式.
【详解】依题意,原式.
故答案为:
【点睛】本小题主要考查复数乘方和除法运算,属于基础题.
15.过抛物线焦点作直线交抛物线于两点,若线段中点的横坐标为3,则等于___________.
【答案】8
【解析】
试题分析:抛物线的焦点为,设所作直线为,联立方程整理得
,方程为
考点:直线与抛物线相交问题
点评:过抛物线焦点的弦与抛物线交于,则焦点弦长为
16.已知函数f(x)=x+,g(x)=2x+a,若∀∈,∈[2,3]都有,则实数a的取值范围是__________
【答案】
【解析】
【分析】
分别求得在区间上的最小值、在区间上的最大值,由此列不等式,解不等式求得的取值范围.
【详解】由于时,,当且仅当,即时等号成立,也即在区间上的最小值为.由于时,单调递增,所以最大值为
由于对,都有,所以,解得.所以实数的取值范围是.
故答案为:.
【点睛】本小题主要考查不等式恒成立问题的求解,考查函数最值的求法,属于中档题.
三、解答题:,共70分,解答应写出文字说明,证明过程或演算步骤.
17.已知函数,其中,且曲线在点处的切线垂直于直线.
(1)求的值;
(2)求函数的单调区间与极值.
【答案】(1) (2) 在(0,5)内为减函数;在(5,+∞)内为增函数. 极小值f(5)=-ln 5.无极大值.
【解析】
试题分析:(1)由曲线y=f(x)在点(1,f(1))处的切线垂直于直线可得
,可求出a的值;(2)根据(1)可得函数的解析式和导函数的解析式,分析导函数的符号,进而可得函数f(x)的单调区间与极值.
试题解析:(1)对求导得,由在点处的切线垂直于直线知,解得.
(2)由(1)知,则,
令,解得或.因为不在的定义域内,故舍去.
当时,,故在上为减函数;
当时,,故在上为增函数.
由此知函数在时取得极小值,.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值
18.某初级中学共有学生2000名,各年级男生、女生人数如表: 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.
初一年级
初二年级
初三年级
女生
373
x
y
男生
377
370
z
(1)求x的值.
(2)现用分层抽样法全校抽取48名学生,问应在初三年级学生中抽取多少名?
(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.
【答案】(1);(2)名;(3)
【解析】
【分析】
(1)利用 “全校学生中随机抽取1名,抽到的是初二年级女生的概率”列方程,解方程求得的值.
(2)利用分层抽样的抽样比,计算出在初三年级学生中抽取的人数.
(3)利用列举法和古典概型概率计算公式,计算出初三年级女生比男生多的概率.
【详解】(1)依题意,所以.
(2)由初一、初二学生人数为,所以初三学生人数为人,故用分层抽样法在全校抽取名学生,问应在初三年级学生中抽取名.
(3)由(2)可知,而,所以初三女生和男生人数的可能取值有:共种,其中女生比男生多的为共种,故初三年级女生比男生多的概率为.
【点睛】本小题主要考查分层抽样的有关计算,考查古典概型的计算,属于基础题.
19.已知函数.
(1)若是的极值点,求及在上的最大值;
(2)若函数是上的单调递增函数,求实数的取值范围.
【答案】(1),在上的最大值为15;
(2)实数的取值范围为:.
【解析】
试题分析:(1)先对函数求导,再把代入导函数使之为0,即解得的值,进一步可求;令导函数为0,列表可求在上的最大值;(2)函数是上的单调递增函数可转化为在R上恒成立,即可求出实数的取值范围.
试题解析:(1),令,即∴.
∴4分
令,解得或(舍去).
当变化时,,,的变化情况如下表:
1
(1,3)
3
(3,5)
5
0
+
1
单调递减↘
9
单调递增↗
15
因此,当时,在区间[1,5]上有最大值是. 8分
(2)是R上的单调递增函数转化为在R上恒成立, 10分
从而有,由,解得12分
考点:导函数的应用、恒成立问题、函数与方程思想.
20.已知离心率为 的椭圆(a>b>0)过点M(,1).
(1)求椭圆的方程.
(2)已知与圆x2+y2=相切的直线l与椭圆C相交于不同两点A,B,O为坐标原点,求的值.
【答案】(1);(2)
【解析】
【分析】
(1)根据椭圆离心率、点的坐标以及列方程组,解方程求得,由此求得椭圆方程.
(2)设出直线的方程,联立直线的方程和椭圆方程,写出韦达定理,结合直线与圆相切,计算出的值.
【详解】(1)因为椭圆过点,且离心率为,所以煤核儿,所以椭圆方程为.
(2)当直线斜率存在时,设直线的方程为,直线与椭圆交于不同的两点,由直线与圆相切得,即,所以①.联立直线的方程和椭圆方程得,消去并化简得,则,即.由根与系数关系得.从而.所以,将①代入上式得.
当直线斜率不存在时,由于直线与圆相切,所以直线的方程为,此时直线与椭圆的两个交点为,或,满足.
综上所述,.
【点睛】本小题主要考查椭圆标准方程的求法,考查直线和椭圆的位置关系,考查直线和圆的位置关系,考查运算求解能力,属于中档题.
21.已知函数 ,
(1)求 的图象在 处的切线方程并求函数 的单调区间;
(2)求证: .
【答案】(1)切线方程为: ,单调增区间为,单调减区间是(2)见解析
【解析】
试题分析:
(1)由函数的导函数可得切线的斜率为2,据此可得切线方程为: ,单调增区间为,单调减区间是;
(2)构造新函数,结合函数的性质即可证得题中的结论.
试题解析:
(1) ,∴,
所以切线方程为:
单调增区间为,单调减区间是
(2)设,.
∵在上单调递增,且,.
∴存在唯一的零点,使得,
即
∴在上单调递减,在单调递增,
∴
=,
又,∴上式等号不成立,∴,即
22.已知椭圆C:()的短轴长为2,离心率为
(1)求椭圆C的方程
(2)若过点M(2,0)的引斜率为的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足(O为坐标原点),当时,求实数的取值范围?
【答案】(1);(2).
【解析】
【分析】
(1)根据椭圆离心率、短轴长以及列方程组,解方程求得,由此求得椭圆方程.
(2)设出直线的方程,联立直线的方程和椭圆方程,写出判别式和韦达定理.计算出弦长,由,求得的一个取值范围.利用求得关于的表达式,根据的取值范围,求得的取值范围.
【详解】(1)由于椭圆的短轴长为,离心率为,所以,解得,所以椭圆的方程为.
(2)设,设直线的方程为,由消去并化简得,,化简得.且.
,由弦长公式得
,两边平方并化简得,解得.
所以.
设,则由得,所以,根据,得.所以,代入椭圆方程并化简得.由于,所以,,所以,所以.
【点睛】本小题主要考查椭圆的方程,考查向量的坐标运算,考查直线和椭圆的位置关系,考查韦达定理的运用,考查运算求解能力,属于难题.