高二数学同步单元练习（必修2） 专题03 空间几何体的表面积与体积（a卷） word版含解析 9页

（测试时间：120 分钟 满分：150 分） 第Ⅰ卷（共 60 分） 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1. 如图，ABC－A′B′C′是体积为 1 的棱柱，则四棱锥 C－AA′B′B 的体积是( ) A.1 3 B.1 2 C.2 3 D.3 4 解析：选 C ∵VC－A′B′C′＝1 3 V 柱＝1 3 ， ∴VC－AA′B′B＝1－1 3 ＝2 3 . 2． 如果轴截面为正方形的圆柱的侧面积是 4π，那么圆柱的体积等于( ) A．π B．2π C．4π D．8π 3． 如图，网格纸上小正方形的边长为 1，粗线画出的是某几何体的三视图，则此几何体的体 积为( ) A．6 B．9 C．12 D．18 解析：选 B 由三视图可知该几何体为底面是斜边为 6 的等腰直角三角形，高为 3 的三棱锥， 其体积为1 3 ×1 2 ×6×3×3＝9. 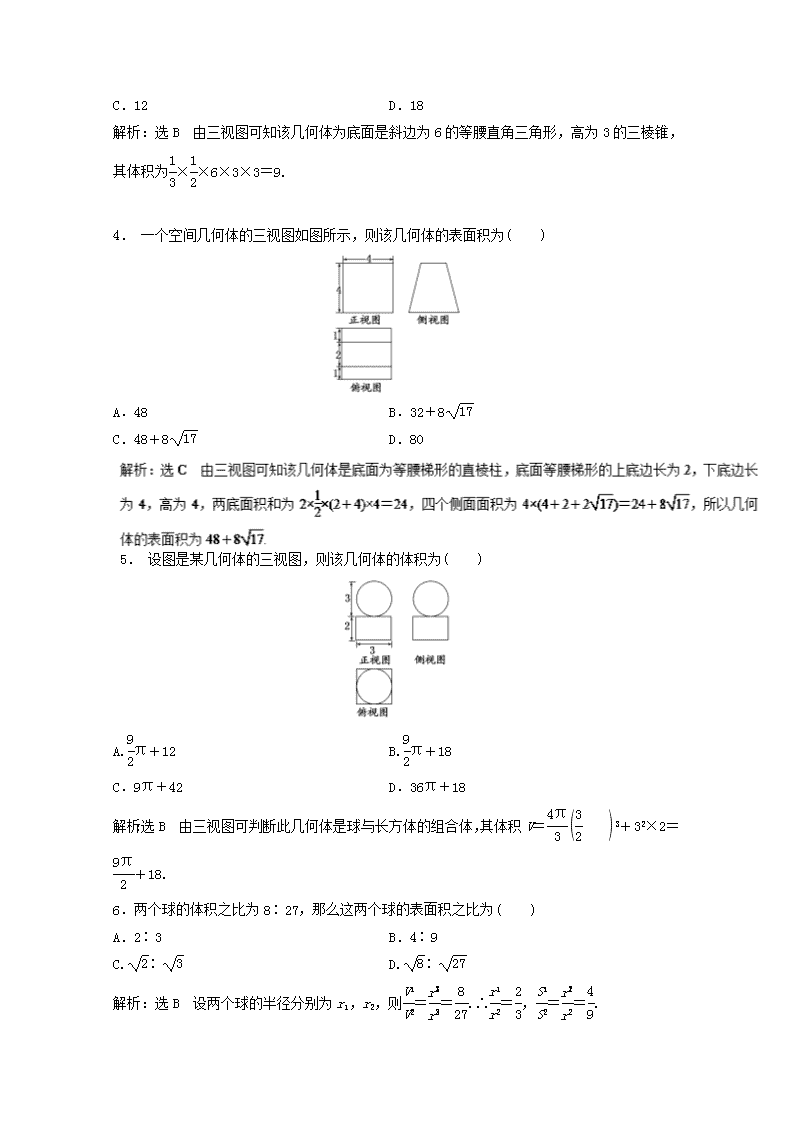4． 一个空间几何体的三视图如图所示，则该几何体的表面积为( ) A．48 B．32＋8 17 C．48＋8 17 D．80 5． 设图是某几何体的三视图，则该几何体的体积为( ) A.9 2 π＋12 B.9 2 π＋18 C．9π＋42 D．36π＋18 解析：选 B 由三视图可判断此几何体是球与长方体的组合体，其体积 V＝4π 3 3 2 3＋32×2＝9π 2 ＋18. 6．两个球的体积之比为 8∶27，那么这两个球的表面积之比为( ) A．2∶3 B．4∶9 C. 2∶ 3 D. 8∶ 27 解析：选 B 设两个球的半径分别为 r1，r2，则V1 V2 ＝r3 1 r3 2 ＝ 8 27 .∴r1 r2 ＝2 3 ，S1 S2 ＝r2 1 r2 2 ＝4 9 . 7．用与球心距离为 1 的平面去截球，所得截面圆的面积为π，则球的表面积为( ) A.8π 3 B.32π 3 C．8π D.8 2π 3 解析：选 C 设球的半径为 R，则截面圆的半径为 R2－1，∴截面圆的面积为 S＝π( R2－1)2 ＝(R2－1)π＝π，∴R2＝2，∴球的表面积 S＝4πR2＝8π. 8．设长方体的长、宽、高分别为 2a、a、a，其顶点都在一个球面上，则该球的表面积为( ) A．3πa2 B．6πa2 C．12πa2 D．24πa2 解析：选 B 由于长方体的长、宽、高分别为 2a、a、a，则长方体的体对角线为 2a 2＋a2＋a2 ＝ 6a，又长方体的外接球的直径 2R 等于长方体的体对角线，所以 2R＝ 6a，则 S 球＝4πR2 ＝4π 6 2 a 2＝6πa2. 9．如果一个球的外切圆锥的高是这个球的半径的 3 倍，则圆锥的侧面面积和球的表面积之比 为( ) A．4∶3 B．3∶1 C．3∶2 D．9∶4 解析：选 C 作轴截面如图，则 PO＝2OD，∠CPB＝30°，CB＝ 3 3 PC＝ 3r，PB＝2 3r，圆锥 侧面积 S1＝6πr2，球的面积 S2＝4πr2，S1∶S2＝3∶2. 10． 平面α截球 O 的球面所得圆的半径为 1，球心 O 到平面α的距离为 2，则此球的体积为 ( ) A. 6π B．4 3π C．4 6π D．6 3π 11．已知长方体的长、宽、高分别是 3，4，5，且它的 8 个顶点都在同一球面上，则这个球的 表面积是( ) A．25π B．50π C． 125π D．都不对 B 由题意知球为长方体的外接球．设球的半径为 R，则(2R)2＝32＋42＋52，∴R2＝25 2 ，∴S 球 ＝4πR2＝4π×25 2 ＝50π. 12．一个空间几何体的三视图如图 L135 所示，其中正视图为等腰直角三角形，侧视图与俯 视图均为正方形，则该几何体的体积和表面积分别为( ) 图 L135 A．64，48＋16 2 B．32，48＋16 2 C.64 3 ，32＋16 2 D.32 3 ，48＋16 2 B 由三视图可知，该几何体是一个三棱柱，其直观图如图所示． 体积 V＝1 2 ×4×4×4＝32，表面积 S＝2×1 2 ×42＋4×(4＋4＋4 2)＝48＋16 2. 第Ⅱ卷（共 90 分） 二、填空题（本大题共 4 小题，每题 5 分，满分 20 分，将答案填在答题纸上） 13． 如图，正方体 ABCD－A1B1C1D1 的棱长为 1，E、F 分别为线段 AA1、B1C 上的点，则三棱锥 D1－EDF 的体积为________． 14．一个正四棱台，其上、下底面均为正方形，边长分别为 8 cm 和 18 cm，侧棱长为 13 cm， 则其表面积为________． 解析：由已知可得正四棱台侧面梯形的高为 h＝ 132－ 18－8 2 2＝12 (cm)， 所以 S 侧＝4×1 2 ×(8＋18)×12＝624 (cm2)，S 上底＝8×8＝64(cm2)，S 下底＝18×18＝324(cm2)， 于是表面积为 S＝624＋64＋324＝1 012(cm2)． 答案：1 012 cm2 15． 圆柱形容器的内壁底半径是 10 cm，有一个实心铁球浸没于容器的水中，若取出这个铁 球，测得容器的水面下降了5 3 cm，则这个铁球的表面积为________ cm2. 解析：设该铁球的半径为 r，则由题意得4 3 πr3＝π×102×5 3 ，解得 r3＝53，∴r＝5，∴这个铁 球的表面积 S＝4π×52＝100π(cm2)． 答案：100π 16．球内切于正方体的六个面，正方体的棱长为 a，则球的表面积为________． 答案：πa2 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17．如图是某几何体的三视图． (1)画出它的直观图(不要求写画法)； (2)求这个几何体的表面积和体积． 解：(1)这个几何体的直观图如图所示． (2)这个几何体是一个简单组合体，它的下部是一个圆柱(底面半径为 1，高为 2)，它的上部 是一个圆锥(底面半径为 1，母线长为 2，高为 3)，所以所求表面积为 S＝π×12＋2π×1×2 ＋π× 1×2＝7π，体积为 V＝π×12×2＋1 3 ×π×12× 3＝2π＋ 3 3 π. 18．已知正三棱锥 V－ABC 的正视图、俯视图如图所示，其中 VA＝4，AC＝2 3，求该三棱锥的 表面积． 解：由正视图与俯视图可得正三棱锥的直观图如图所示， 且 VA＝VB＝VC＝4，AB＝BC＝AC＝2 3. 取 BC 的中点 D，连接 VD， 则 VD⊥BC，有 VD＝ VB2－BD2＝ 42－ 3 2＝ 13， 则 S△VBC＝1 2 ×VD×BC＝1 2 × 13×2 3＝ 39， S△ABC＝1 2 ×(2 3)2× 3 2 ＝3 3， 所以，三棱锥 V－ABC 的表面积为 3S△VBC＋S△ABC＝3 39＋3 3＝3( 39＋ 3)． 19． 一个几何体的三视图如图所示(单位：m)，则该几何体的体积为多少？ 该几何体的体积 V＝2V 球＋V 长方体 ＝2×4 3 π 3 2 3＋6×1×3 ＝18＋9π. 20．某组合体的直观图如图所示，它的中间为圆柱形，左右两端均为半球形，若图中 r＝1，l ＝3，试求该组合体的表面积和体积． 解：该组合体的表面积 S＝4πr2＋2πrl＝4π×12＋2π×1×3＝10π，该组合体的体积 V＝4 3 πr3＋πr2l＝4 3 π×13＋ π×12×3＝13π 3 . 21．(2012·潍坊高一检测)用两个平行平面去截半径为 R 的球面，两个截面圆的半径为 r1＝ 24 cm，r2＝15 cm，两截面间的距离为 d＝27 cm，求球的表面积． ∴S 球＝4πR2＝2 500π(cm2)． 22．如图所示，在四边形 ABCD 中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝2 2，AD＝2， 求四边形 ABCD 绕 AD 所在直线旋转一周所成的几何体的表面积及体积． 解：易知所得的几何体是由一个圆台截去一个圆锥所得的组合体， 且 CE＝DE＝AD＝2，BC＝5，则 S 表面＝S 圆台底面＋S 圆台侧面＋S 圆锥侧面＝π×52＋π×(2＋5)×5＋π× 2×2 2＝60π＋4 2π， V＝V 圆台－V 圆锥＝1 3 π(22＋2×5＋52)×4－1 3 π×22×2＝148 3 π.