2012年四川高考试题（理数解析版） 13页

‎2012年普通高等学校招生全国统一考试（四川卷）‎ 数学（理科） ‎ 参考公式：‎ 如果事件互斥，那么 球的表面积公式 ‎ ‎ 如果事件相互独立，那么 其中表示球的半径 ‎ 球的体积公式 如果事件在一次试验中发生的概率是，那么 ‎ 在次独立重复试验中事件恰好发生次的概率 其中表示球的半径 第一部分 （选择题 共60分）‎ 注意事项：‎ ‎1、选择题必须使用2B铅笔将答案标号涂在机读卡上对应题目标号的位置上。‎ ‎2、本部分共12小题，每小题5分，共60分。‎ 一、选择题：每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1、的展开式中的系数是（ ）‎ A、 B、 C、 D、‎ ‎[答案]D ‎ ‎[解析]二项式展开式的通项公式为=，令k=2，则 ‎[点评]：高考二项展开式问题题型难度不大，要得到这部分分值，首先需要熟练掌握二项展开式的通项公式，其次需要强化考生的计算能力.‎ ‎2、复数（ ）‎ A、 B、 C、 D、‎ ‎[答案]B. ‎ ‎[解析]‎ ‎[点评]突出考查知识点，不需采用分母实数化等常规方法，分子直接展开就可以.‎ ‎3、函数在处的极限是（ ）‎ A、不存在 B、等于 C、等于 D、等于 ‎[答案]A ‎ ‎[解析]分段函数在x=3处不是无限靠近同一个值，故不存在极限.‎ ‎[点评]对于分段函数，掌握好定义域的范围是关键。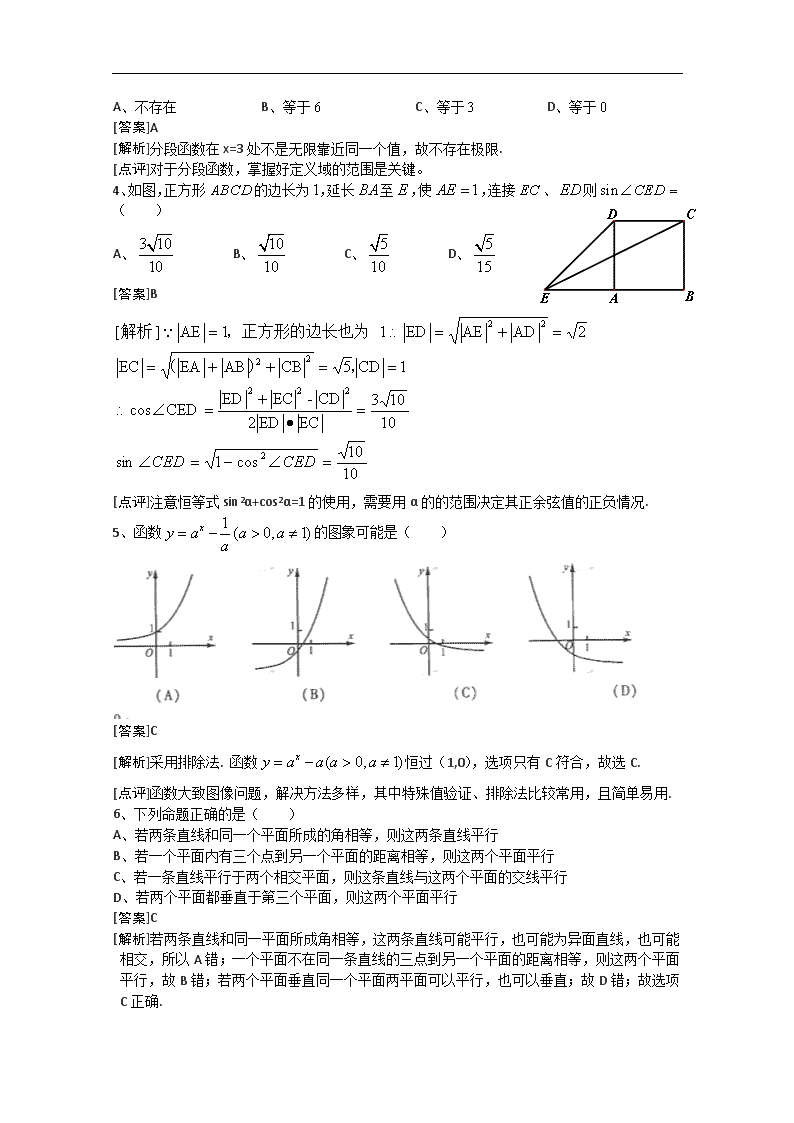‎ ‎4、如图，正方形的边长为，延长至，使，连接、则（ ）‎ A、 B、 C、 D、 ‎ ‎[答案]B ‎ ‎[点评]注意恒等式sin2α+cos2α=1的使用，需要用α的的范围决定其正余弦值的正负情况.‎ ‎5、函数的图象可能是（ ）‎ ‎[答案]C ‎[解析]采用排除法. 函数恒过（1,0），选项只有C符合，故选C.‎ ‎[点评]函数大致图像问题，解决方法多样，其中特殊值验证、排除法比较常用，且简单易用.‎ ‎6、下列命题正确的是（ ）‎ A、若两条直线和同一个平面所成的角相等，则这两条直线平行 B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D、若两个平面都垂直于第三个平面，则这两个平面平行 ‎[答案]C ‎[解析]若两条直线和同一平面所成角相等，这两条直线可能平行，也可能为异面直线，也可能相交，所以A错；一个平面不在同一条直线的三点到另一个平面的距离相等，则这两个平面平行，故B错；若两个平面垂直同一个平面两平面可以平行，也可以垂直；故D错；故选项C正确.‎ ‎[点评]本题旨在考查立体几何的线、面位置关系及线面的判定和性质，需要熟练掌握课本基础知识的定义、定理及公式.‎ ‎7、设、都是非零向量，下列四个条件中，使成立的充分条件是（ ）‎ A、 B、 C、 D、且 ‎[答案]D ‎[解析]若使成立，则选项中只有D能保证，故选D.‎ ‎[点评]本题考查的是向量相等条件模相等且方向相同.学习向量知识时需注意易考易错零向量，其模为0且方向任意.‎ ‎8、已知抛物线关于轴对称，它的顶点在坐标原点，并且经过点。若点到该抛物线焦点的距离为，则（ ）‎ A、 B、 C、 D、‎ ‎[答案]B ‎ ‎[解析]设抛物线方程为y2=2px(p>0),则焦点坐标为（），准线方程为x=, ‎ ‎[点评]本题旨在考查抛物线的定义: |MF|=d,(M为抛物线上任意一点，F为抛物线的焦点，d为点M到准线的距离).‎ ‎9、某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗原料‎1千克、原料‎2千克；生产乙产品1桶需耗原料‎2千克，原料‎1千克。每桶甲产品的利润是300元，每桶乙产品的利润是400元。公司在生产这两种产品的计划中，要求每天消耗、原料都不超过12千克。通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（ ）‎ A、1800元 B、2400元 C、2800元 D、3100元 ‎[答案]C ‎[解析]设公司每天生产甲种产品X桶，乙种产品Y桶，公司共可获得 利润为Z元/天，则由已知，得 Z=300X+400Y 且 画可行域如图所示，‎ 目标函数Z=300X+400Y可变形为 Y= 这是随Z变化的一族平行直线 解方程组 即A（4,4） ‎ ‎[点评]解决线性规划题目的常规步骤：一列（列出约束条件）、二画（画出可行域）、三作（作目标函数变形式的平行线）、四求（求出最优解）.‎ ‎10、如图，半径为的半球的底面圆在平面内，过点作平面的垂线交半球面于点，过圆的直径作平面成角的平面与半球面相交，所得交线上到平面的距离最大的点为，该交线上的一点满足，则、两点间的球面距离为（ ）‎ A、 B、 C、 D、‎ ‎[答案]A ‎[解析] 以O为原点，分别以OB、OC、OA所在直线为x、y、z轴，‎ 则A ‎[点评]本题综合性较强，考查知识点较为全面，题设很自然的把向量、立体几何、三角函数等基础知识结合到了一起.是一道知识点考查较为全面的好题.要做好本题需要有扎实的数学基本功.‎ ‎11、方程中的，且 互不相同，在所有这些方程所表示的曲线中，不同的抛物线共有（ ）‎ A、60条 B、62条 C、71条 D、80条 ‎[答案]B ‎[解析]方程变形得，若表示抛物线，则 所以，分b=-3,-2,1,2,3五种情况：‎ ‎（1）若b=-3， ; （2）若b=3, ‎ 以上两种情况下有9条重复，故共有16+7=23条；‎ 同理当b=-2,或2时，共有23条； 当b=1时，共有16条.‎ 综上，共有23+23+16=62种 ‎[点评]此题难度很大，若采用排列组合公式计算，很容易忽视重复的18条抛物线. 列举法是解决排列、组合、概率等非常有效的办法.要能熟练运用.‎ ‎12、设函数，是公差为的等差数列，，则（ ）‎ A、 B、 C、 D、‎ ‎[答案]D ‎[解析]∵数列{an}是公差为的等差数列，且 ‎∴‎ ‎∴ 即 ‎ 得 ‎∴‎ ‎[点评]本题难度较大，综合性很强.突出考查了等差数列性质和三角函数性质的综合使用，需考生加强知识系统、网络化学习. 另外，隐蔽性较强，需要考生具备一定的观察能力.‎ 第二部分 （非选择题 共90分）‎ 注意事项：‎ ‎（1）必须使用0.5毫米黑色签字笔在答题卡上题目所指示的答题区域内作答，作图题可先用铅笔绘出，确认后再用0.5毫米黑色签字笔描清楚。答在试题卷上无效。‎ ‎（2）本部分共10个小题，共90分。‎ 二、填空题（本大题共4个小题，每小题4分，共16分。把答案填在答题纸的相应位置上。）‎ ‎13、设全集，集合，，则_______。‎ ‎[答案]{a, c, d}‎ ‎[解析]∵ ； ∴{a,c，d}‎ ‎[点评]本题难度较低，只要稍加注意就不会出现错误.‎ ‎14、如图，在正方体中，、分别是、的中点，则异面直线与所成角的大小是____________。‎ ‎[答案]90º ‎[解析]方法一：连接D‎1M,易得DN⊥A1D1 ,DN⊥D‎1M, ‎ 所以，DN⊥平面A1MD1，‎ 又A1M平面A1MD1，所以，DN⊥A1D1，故夹角为90º 方法二：以D为原点，分别以DA, DC, DD1为x, y, z轴，建立空间直角坐标系D—xyz.设正方体边长为2，则D（0,0,0），N（0,2,1），M（0,1,0）A1（2,0,2）‎ 故，‎ 所以，cos< = 0,故DN⊥D1M，所以夹角为90º ‎[点评]异面直线夹角问题通常可以采用两种途径: 第一，把两条异面直线平移到同一平面中借助三角形处理； 第二，建立空间直角坐标系，利用向量夹角公式解决.‎ ‎ 15、椭圆的左焦点为，直线与椭圆相交于点、，当的周长最大时，的面积是____________。‎ ‎[答案] ‎ ‎[解析]根据椭圆定义知：‎4a=12, 得a=3 , 又 ‎[点评]本题考查对椭圆概念的掌握程度.突出展现高考前的复习要回归课本的新课标理念.‎ ‎16、记为不超过实数的最大整数，例如，，，。设为正整数，数列满足，，现有下列命题：‎ ‎①当时，数列的前3项依次为5,3,2；‎ ‎②对数列都存在正整数，当时总有；‎ ‎③当时，；‎ ‎④对某个正整数，若，则。‎ 其中的真命题有____________。（写出所有真命题的编号）‎ ‎[答案]①③④（lby lfx）‎ ‎[解析]若，根据 ‎ 当n=1时，x2=[]=3, 同理x3=, 故①对.‎ 对于②③④可以采用特殊值列举法：‎ 当a=1时，x1=1, x2=1, x3=1, ……xn=1, …… 此时②③④均对.‎ 当a=2时，x1=2, x2=1, x3=1, ……xn=1, …… 此时②③④均对 当a=3时，x1=3, x2=2, x3=1, x4=2……xn=1, ……此时③④均对 综上，真命题有 ①③④ .‎ ‎[点评]此题难度较大，不容易寻找其解题的切入点，特殊值列举是很有效的解决办法.‎ 三、解答题（本大题共6个小题，共74分。解答应写出必要的文字说明，证明过程或演算步骤。）‎ ‎17、(本小题满分12分) ‎ ‎ 某居民小区有两个相互独立的安全防范系统（简称系统）和，系统和在任意时刻发生故障的概率分别为和。‎ ‎（Ⅰ）若在任意时刻至少有一个系统不发生故障的概率为，求的值；‎ ‎（Ⅱ）设系统在3次相互独立的检测中不发生故障的次数为随机变量，求的概率分布列及数学期望。‎ ‎[解析]（1）设：“至少有一个系统不发生故障”为事件C，那么 ‎1-P（C）=1-P= ，解得P=………………………………4 分 ‎ ‎（2）由题意，P（=0）=‎ P（=1）=‎ P（=2）=‎ P（=3）=‎ 所以，随机变量的概率分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎ ‎ ‎ P 故随机变量X的数学期望为：‎ E=0 ……………………12分.‎ ‎[点评]本小题主要考查相互独立事件，独立重复试验、互斥事件、随机变量的分布列、数学期望等概念及相关计算，考查运用概率知识与方法解决实际问题的能力.‎ ‎18、(本小题满分12分) ‎ ‎ 函数在一个周期内的图象如图所示，为图象的最高点，、为图象与轴的交点，且为正三角形。‎ ‎（Ⅰ）求的值及函数的值域；‎ ‎（Ⅱ）若，且，求的值。‎ ‎[解析]（Ⅰ）由已知可得：‎ ‎ =3cosωx+‎ 又由于正三角形ABC的高为2，则BC=4‎ 所以，函数 所以，函数。……………………6分 ‎（Ⅱ）因为（Ⅰ）有 ‎ ‎ 由x0‎ 所以，‎ 故 ‎ ‎ ‎ ………………………………………………………12分 ‎[点评]本题主要考查三角函数的图像与性质同三角函数的关系、两角和的正（余）弦公式、二倍角公式等基础知识，考查运算能力，考查树形结合、转化等数学思想.‎ ‎19、(本小题满分12分) ‎ ‎ 如图，在三棱锥中，，，，平面平面。‎ ‎（Ⅰ）求直线与平面所成角的大小；‎ ‎（Ⅱ）求二面角的大小。‎ ‎[解析]（1）连接OC。由已知，所成的角 设AB的中点为D，连接PD、CD.‎ 因为AB=BC=CA,所以CDAB.‎ 因为等边三角形，‎ 不妨设PA=2，则OD=1，OP=,AB=4.‎ 所以CD=2，OC=.‎ 在Rttan.‎ 故直线PC与平面ABC所成的角的大小为arctan…………………6分 ‎（2）过D作DE于E，连接CE. ‎ ‎ 由已知可得，CD平面PAB.‎ 根据三垂线定理可知，CE⊥PA，‎ 所以，.‎ 由（1）知，DE=‎ 在Rt△CDE中，tan 故……………………………12分 ‎[点评]本小题主要考查线面关系、直线与平面所成的角、二面角等基础知识，考查思维能力、空间想象能力，并考查应用向量知识解决数学问题的能力.‎ ‎20、(本小题满分12分) 已知数列的前项和为，且对一切正整数都成立。‎ ‎（Ⅰ）求，的值；‎ ‎（Ⅱ）设，数列的前项和为，当为何值时，最大？并求出的最大值。‎ ‎[解析]取n=1,得 ①‎ ‎ 取n=2,得 ②‎ 又②-①，得 ③‎ ‎（1）若a2=0, 由①知a1=0, ‎ ‎ (2)若a2, ④‎ 由①④得：…………………5分 ‎（2）当a1>0时,由（I）知，‎ 当 , (2+)an-1=S2+Sn-1‎ 所以，an=‎ 所以 令 所以，数列{bn}是以为公差，且单调递减的等差数列.‎ 则 b1>b2>b3>…>b7=‎ 当n≥8时，bn≤b8=‎ 所以，n=7时，Tn取得最大值，且Tn的最大值为 T7=…………………………12分 ‎[点评]本小题主要从三个层面对考生进行了考查. 第一，知识层面：考查等差数列、等比数列、对数等基础知识；第二，能力层面：考查思维、运算、分析问题和解决问题的能力；第三，数学思想：考查方程、分类与整合、化归与转化等数学思想.‎ ‎21、(本小题满分12分) 如图，动点到两定点、构成，且，设动点的轨迹为。‎ ‎（Ⅰ）求轨迹的方程；‎ ‎（Ⅱ）设直线与轴交于点，与轨迹相交于点，且，求的取值范围。‎ ‎[解析]（1）设M的坐标为（x,y），显然有x>0,.‎ 当∠MBA=90°时，点M的坐标为（2，, ±3）‎ 当∠MBA≠90°时；x≠2.由∠MBA=2∠MAB,‎ 有tan∠MBA=,即 化简得：3x2-y2-3=0,而又经过（2，,±3）‎ 综上可知，轨迹C的方程为3x2-y2-3=0（x>1）…………………5分 ‎(II)由方程消去y，可得。（*）‎ 由题意，方程（*）有两根且均在（1，+）内，设 所以 解得，m>1,且m2‎ 设Q、R的坐标分别为，由有 所以 由m>1，且m2，有 所以的取值范围是................................................ 12分 ‎[点评]本小题主要考察直线、双曲线、轨迹方程的求法等基础知识，考察思维能力、运算能力，考察函数、分类与整合等思想，并考察思维的严谨性。‎ ‎ 22、(本小题满分14分) （lb ylfx）‎ ‎ 已知为正实数，为自然数，抛物线与轴正半轴相交于点，设为该抛物线在点处的切线在轴上的截距。‎ ‎（Ⅰ）用和表示；‎ ‎（Ⅱ）求对所有都有成立的的最小值；‎ ‎（Ⅲ）当时，比较与的大小，并说明理由。‎ ‎[解析]（1）由已知得，交点A的坐标为，对则抛物线在点A处的切线方程为 （2） 由（1）知f(n)=,则 即知，对于所有的n成立，特别地，取n=2时，得到a≥‎ 当,‎ ‎>2n3+1‎ 当n=0,1,2时，显然 故当a=时，对所有自然数都成立 所以满足条件的a的最小值是。‎ ‎（3）由（1）知，则，‎ 下面证明：‎ 首先证明：当0