2020届艺术生高考数学二轮复习课时训练：第六章 不等式、推理与证明 第3节 5页

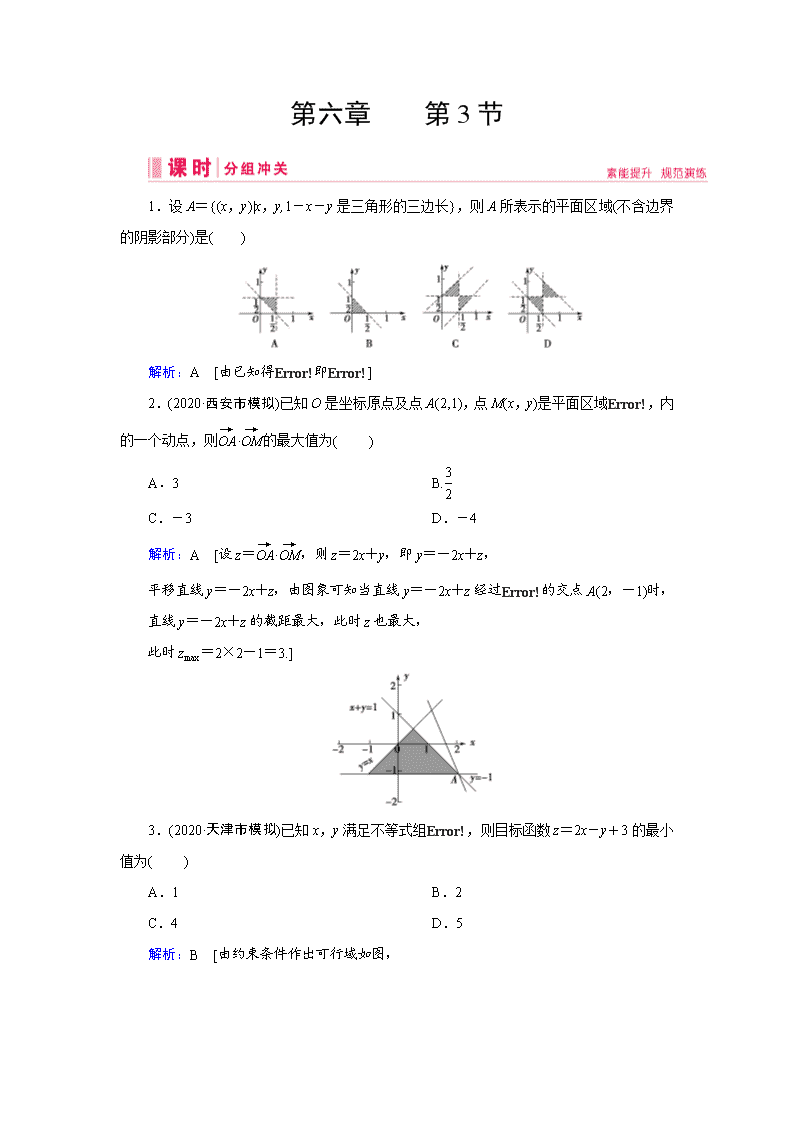
第六章 第3节 ‎1．设A＝{(x，y)|x，y,1－x－y是三角形的三边长}，则A所表示的平面区域(不含边界的阴影部分)是(　　)‎ 解析：A　[由已知得即]‎ ‎2．(2020·西安市模拟)已知O是坐标原点及点A(2,1)，点M(x，y)是平面区域，内的一个动点，则·的最大值为(　　 )‎ A．3　　　　　　　　　　　 B. C．－3 D．－4‎ 解析：A　[设z＝·，则z＝2x＋y，即y＝－2x＋z，‎ 平移直线y＝－2x＋z，由图象可知当直线y＝－2x＋z经过的交点A(2，－1)时，‎ 直线y＝－2x＋z的截距最大，此时z也最大，‎ 此时zmax＝2×2－1＝3.]‎ ‎3．(2020·天津市模拟)已知x，y满足不等式组，则目标函数z＝2x－y＋3的最小值为(　　 )‎ A．1 B．2‎ C．4 D．5‎ 解析：B　[由约束条件作出可行域如图，‎ 设可行域内一点(x，y)，‎ 由图可知，直线z＝2x－y＋3经过D点时取到最大值，经过C点时取到最小值，‎ 联立，解得C(0,1)，‎ ‎∴z的最小值为－1＋3＝2.]‎ ‎4．(2020·德州市一模)已知不等式组所表示的平面区域为面积等于的三角形，则实数k的值为(　　 )‎ A．1 B．－2‎ C．1或－2 D．－ 解析：A　[∵不等式组所表示的平面区域为面积等于的三角形，如图：‎ 平面为三角形，且过点(2,0)，‎ ‎∵y＝kx＋1，与x轴的交点为，‎ y＝kx＋1与y＝－x＋2的交点为，‎ 三角形的面积为：××＝，‎ 解得k＝1.]‎ ‎5．(2019·厦门市一模)设x，y满足约束条件，则z＝|x＋3y|的最大值是(　　 )‎ A. B．1‎ C. D．2‎ 解析：D　[画出x，y满足约束条件表示的平面区域，‎ 由解得B，‎ 由解得A(－1,1)，‎ 由解得C.‎ 设目标函数为z′＝x＋3y，作出目标函数对应的直线，‎ 直线过C时，直线的纵截距最小，z′最小，最小值为－；当直线过A(－1,1)时，直线的纵截距最大，z′最大，最大值为2；∴目标函数z＝|x＋3y|的取值范围是[0,2]，最大值为2.]‎ ‎6．(2019·泉州市模拟)若x，y满足约束条件，则z＝x2＋y2的最小值为　_____　.‎ 解析：不等式组表示的平面区域如图所示，‎ 则z＝x2＋y2的几何意义为区域内的点到原点的距离的平方，‎ 由图象知，OA的距离最小，‎ 由，解得A(0,1)，‎ 所以|OA|2＝1，‎ 所以z＝x2＋y2的最小值为1.‎ 答案：1‎ ‎7．若不等式组，表示的平面区域的面积为3，则实数a的值是　________　.‎ 解析：作出可行域，如图中阴影部分所示，区域面积 S＝××2＝3，解得a＝2.‎ 答案：2‎ ‎8．(2019·聊城市一模)设x，y满足约束条件，则z＝2xy的最大值为　________　.‎ 解析：画出约束条件表示的平面区域，如图所示；‎ 又z＝2xy＝2x·2－4y＝2x－4y，‎ 设t＝x－4y，‎ 则目标函数t＝x－4y过点B时，取得最大值，‎ 由，得B(－2，－1)；‎ ‎∴z的最大值为2－2－4×(－1)＝4.‎ 答案：4‎ ‎9．(2019·杭州市高三模拟)若实数x，y满足.‎ 求：(1)x的取值范围；‎ ‎(2)|x|＋|y|的取值范围．‎ 解：‎ ‎(1)由约束条件作出可行域如图，‎ 由图可知，0≤x≤1.‎ ‎(2)当x≥0，y≥0时，‎ z＝|x|＋|y|＝x＋y过时有最大值为，‎ 过O(0,0)时有最小值0；‎ 当x≥0，y≤0时，z＝|x|＋|y|＝x－y过(1，－1)时有最大值为2，‎ 过O(0,0)时有最小值0.所以|x|＋|y|的取值范围是[0,2]．‎ ‎10．若x，y满足约束条件 ‎(1)求目标函数z＝x－y＋的最值；‎ ‎(2)若目标函数z＝ax＋2y仅在点(1,0)处取得最小值，求a的取值范围．‎ 解：(1)作出可行域如图，可求得A(3,4)，B(0,1)，C(1,0)．‎ 平移初始直线x－y＋＝0，过A(3,4)时z取最小值－2，过C(1,0)时z取最大值1.‎ 所以z的最大值为1，最小值为－2.‎ ‎(2)直线ax＋2y＝z仅在点(1,0)处取得最小值，由图象可知－1<－<2，‎ 解得－4