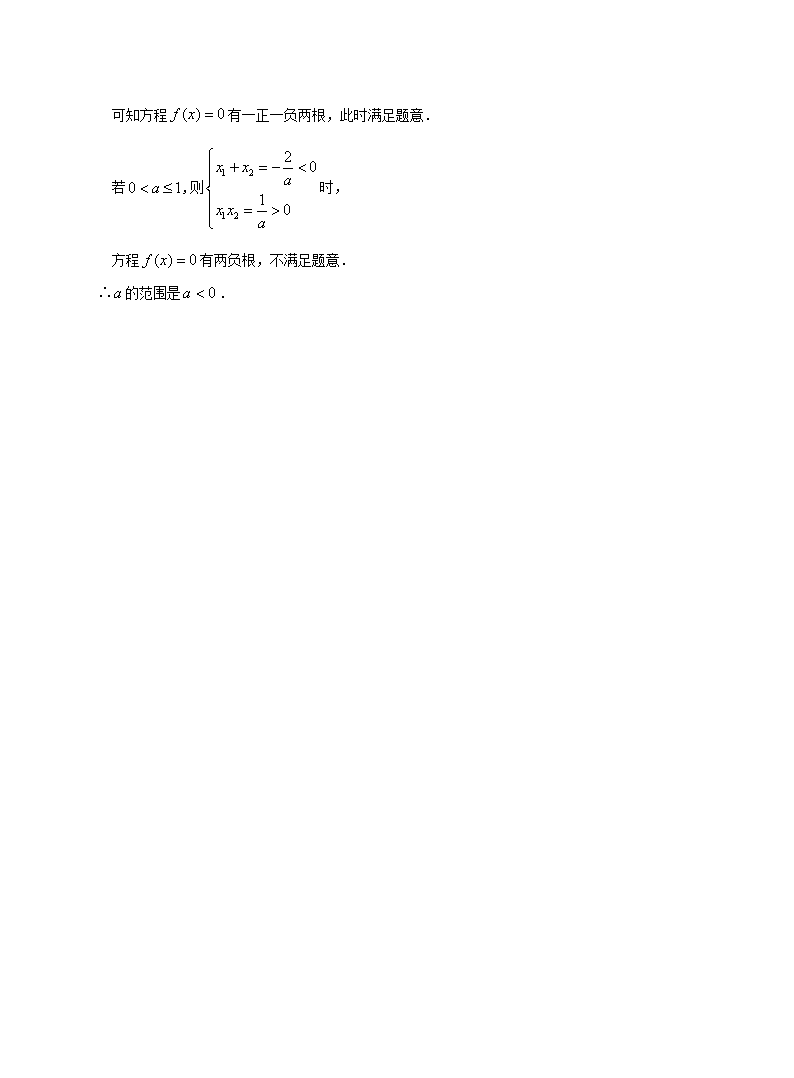- 310.00 KB
- 2021-04-17 发布
第2课 命题与简易逻辑
1.(2019湛江二模)命题“若,则”的逆否命题是( )
A.若“,则 B.若,则
C.若,则 D.若,则
【答案】C
2.(2019湖北高考)命题“,”的否定是( )
A., B.,
C., D.,
【答案】D
3.(2019辽宁高考)已知命题:,,则是( )
A.,
B.,
C.,
D.,
【答案】C
【解析】全称命题的否定形式为将“”改为“”,后面的加以否定.
4.(2019江门一模)下列结论,不正确的是( )
A.若命题:,,则命题:,.
B.若是假命题,是真命题,则命题与命题均为真命题.
C.方程(,是常数)表示双曲线的充要条件是.
D.若角的终边在直线上,且,则这样的角有4个.
【答案】A
【解析】命题:,.
5.(2019东莞二模)对于函数①,②,③,判断如下两个命题的真假:命题甲:是偶函数;命题乙:在上是减函数,在上是增函数;能使命题甲、乙均为真的所有函数的序号是( )
A.①② B.①③ C.② D.③
【答案】C
【解析】对于①,不是偶函数,故命题甲假,
对于③,在上不是减函数,故命题乙假.
6.(2019房山二模)有下列命题:
①在函数的图象中,相邻两个对称中心的距离为;
②函数的图象关于点对称;
③关于的方程有且仅有一个实数根,则实数;
④已知命题:,都有,则是:,使得.
其中真命题的序号是_______.
【答案】③ ④
7.已知函数是上的增函数,,对命题“若,则”.
(1)写出否命题,判断其真假,并证明你的结论;
(2)写出逆否命题,判断其真假,并证明你的结论.
【解析】(1))否命题:已知函数是上的增函数,,对命题“若,则”.
该命题是真命题,证明如下:
又∵在上是增函数.
∴否命题为真命题.
(2)逆否命题:已知函已知函数是上的增函数,,若,则.
真命题,可证明原命题为真来证明它.
∵在上是增函数.
故原命题为真命题,所以逆否命题为真命题.
8.已知函数.
(1)若的图象与轴恰有一个公共点,求的值;
(2)若方程至少有一正根,求的范围.
【解析】(1)当时,图象与轴恰有一个公共点,满足题意.
当时,,即.∴或.
(2)由(1)可知.
当方程有实根时,且.
若,则由,
可知方程有一正一负两根,此时满足题意.
若,则时,
方程有两负根,不满足题意.
∴的范围是.
相关文档
- 广东省广州市广雅中学2020届高三高2021-04-17 20:24:0725页
- 三维设计高考生物一轮复习精品学案2021-04-17 20:24:0713页
- 粤沪版广东中考物理模拟卷九2021-04-17 20:22:288页
- 2018-2019学年广东省北京师范大学2021-04-17 20:20:2710页
- 历史卷·2019届广东省汕头市潮师高2021-04-17 20:18:5711页
- 广东省惠州市2020届高三第三次调研2021-04-17 20:18:2817页
- 数学(文)卷·2019届广东省汕头市达濠2021-04-17 20:17:459页
- 乡村四月小学语文人教课标版四级下2021-04-17 20:15:1152页
- 广东省广州市番禺区2020届高三3月2021-04-17 20:13:0411页
- 广东省阳春市第一中学2019-2020学2021-04-17 20:11:3711页