2019年高考数学考前30天---选择题专训（十九） 8页

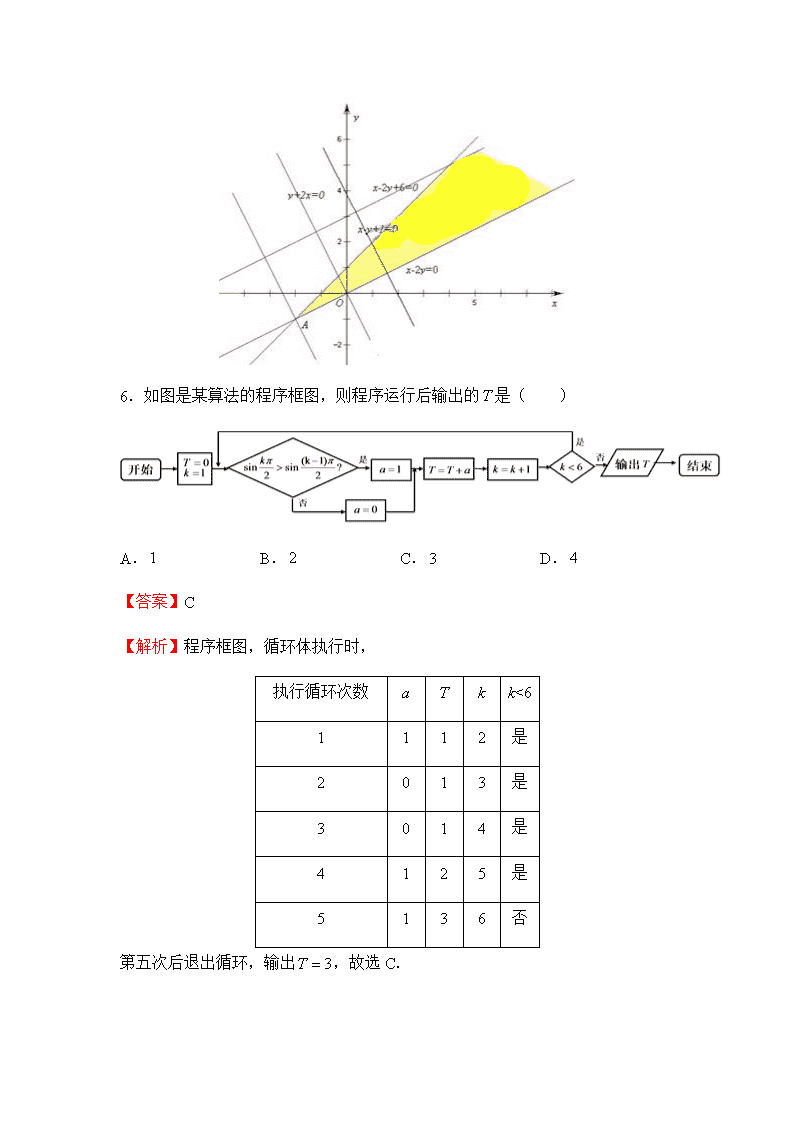
‎2019年高考数学考前30天---选择题专训（十九）‎ 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，则（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】∵集合，，故选C．‎ ‎2．已知，其中，是实数，是虚数单位，则（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】，所以，，所以．‎ ‎3．函数的图象在原点处的切线方程为（ ）‎ A． B． C． D．不存在 ‎【答案】C ‎【解析】函数的导数为，在原点处的切线斜率为，‎ 则在原点处的切线方程为，即为，故选C．‎ ‎4．函数的值域不可能是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】设，则函数为开口向上的抛物线，若判别式，此时函数的值域为，若判别式，则函数恒成立，此时函数有最小值，当时，的值域为；当时，的值域为，故不可能为A．故选A．‎ ‎5．实数，满足，若恒成立，则的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】不等式组表示的平面区域是图中阴影部分（夹在两条平行线和之间且在直线右侧的部分），作直线，平行直线，当它过点时，取得最小值－5，因此所求的范围是，故选B．‎ ‎6．如图是某算法的程序框图，则程序运行后输出的是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】程序框图，循环体执行时，‎ 执行循环次数 a T k k<6‎ ‎1‎ ‎1‎ ‎1‎ ‎2‎ 是 ‎2‎ ‎0‎ ‎1‎ ‎3‎ 是 ‎3‎ ‎0‎ ‎1‎ ‎4‎ 是 ‎4‎ ‎1‎ ‎2‎ ‎5‎ 是 ‎5‎ ‎1‎ ‎3‎ ‎6‎ 否 第五次后退出循环，输出，故选C．‎ ‎7．已知，分别是双曲线的左、右焦点，过点与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点，若点在以线段为直径的圆外，则双曲线离心率的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由已知得，所以，因为点在以为直径的圆外，所以，所以，解得．‎ ‎8．已知，其中为常数．的图象关于直线对称，则在以下区间上是单调函数的是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】的图象关于直线对称，则，即，，，把A、B、C、D分别代入，只有当时，，函数是单调减函数．故选B．‎ ‎9．一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由已知中的三视图可得，该几何体是一个以正视图为底面的四棱锥，其外接球，与以俯视图为底面，以2为高的正三棱柱的外接球相同，如图所示：‎ 由底面边长为，可得底面外接圆的半径为，由棱柱高为，可得球心距为，故外接球半径为，故外接球的表面积为，故选B．‎ ‎10．已知焦点在轴上的椭圆方程为，随着的增大该椭圆的形状（ ）‎ A．越接近于圆 B．越扁 C．先接近于圆后越扁 D．先越扁后接近于圆 ‎【答案】A ‎【解析】椭圆方程为焦点在轴上的椭圆方程，，解得，由于在不断的增大，即离心率不断减小，所以椭圆的形状越来越接近于圆，故选A．‎ ‎11．坐标平面上的点集满足，将点集中的所有点向轴作投影，所得投影线段的长度为（ ）‎ A．1 B． C． D．2‎ ‎【答案】D ‎【解析】∵，∴，‎ 即，∴，‎ ‎∵，∴，∴，∴，‎ ‎∵坐标平面上的点集满足，‎ ‎∴，即，∴或，‎ ‎∴将点集中的所有点向轴作投影，所得投影线段的长度为，故选D．‎ ‎12．已知函数，，若对任意的，存在实数满足，使得，则的最大值为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】当时，作函数与的图象如图，‎ ‎，对，存在实数满足，使得成立，正确；当时，作函数与的图象如图，‎ ‎，对，存在实数，满足，使得 成立，正确；当时，作函数与的图象如图，‎ ‎，对，存在实数满足，使得成立，正确；当时，作函数与的图象如图，‎ ‎，不存在实数满足，使得成立，的最大值为，故选B．‎