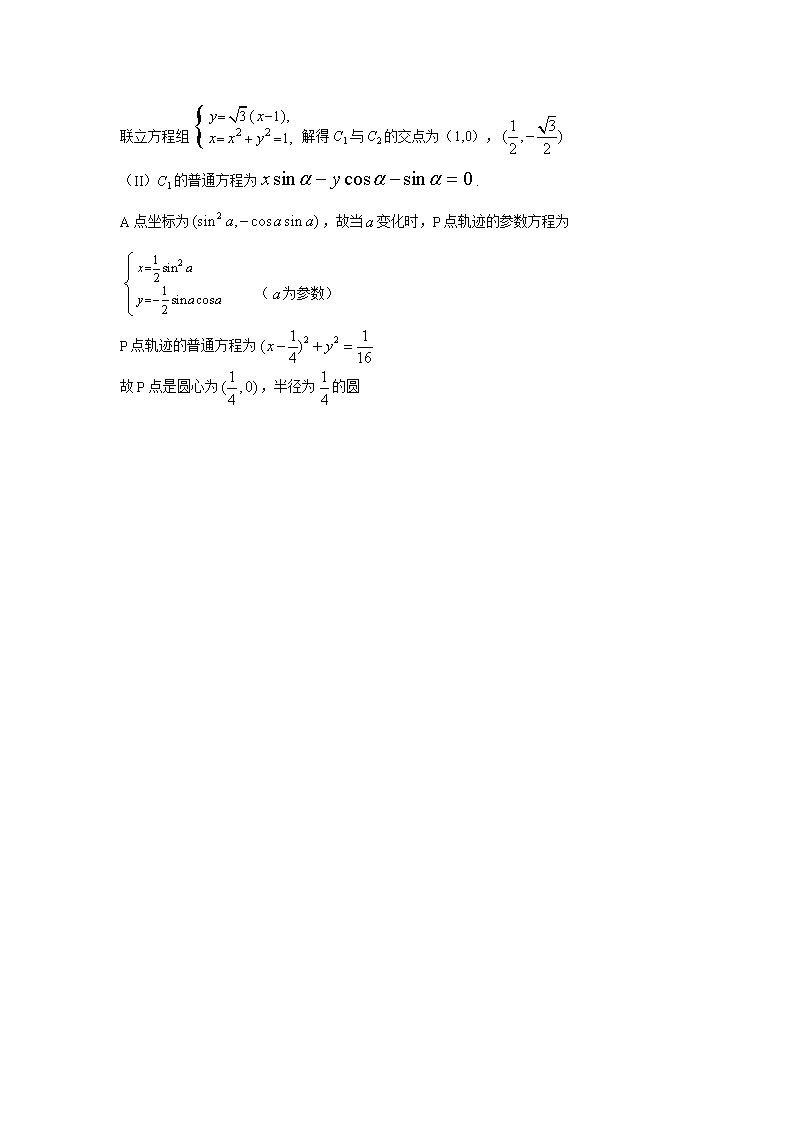高考数学题分类专题22选修44坐标系与参数方程 3页

‎2010年全国各地高考数学真题分章节分类汇编 第22部分:选修系列---（选修4-4：坐标系与参数方程）‎ 一、选择题:‎ ‎1．（2010年高考重庆卷文科8）若直线与曲线（）有两个不同的公共点，则实数的取值范围为 ‎（A） （B）‎ ‎（C） （D）‎ ‎【答案】D ‎【解析】化为普通方程，表示圆，‎ 因为直线与圆有两个不同的交点，所以解得 法2：利用数形结合进行分析得 同理分析，可知 ‎2．（2010年高考湖南卷文科4）极坐标和参数方程（t为参数）所表示的图形分别是 A. 直线、直线 B. 直线、圆 C. 圆、圆 D. 圆、直线 D 二、填空题：‎ ‎1．（2010年高考广东卷文科15）（坐标系与参数方程选做题）在极坐标系中，曲线与的交点的极坐标为 .‎ ‎2．（2010年高考陕西卷文科15）（坐标系与参数方程选做题）参数方程（为参数）化成普通方程为 ‎ .‎ ‎【答案】x2＋（y－1）2＝1‎ 三、解答题：‎ ‎1．（2010年高考辽宁卷文科23）（本小题满分10分）选修4－4：坐标系与参数方程 已知P为半圆C：（为参数，0≤≤）上的点，点A的坐标为（1，0），O为坐标原点，点M在射线OP上，线段OM与C的弧的长度均为.‎ ‎（Ⅰ）以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标;‎ ‎（Ⅱ）求直线AM的参数方程.‎ 解：(Ⅰ)由已知，M点的极角为，且M点的极径等于，‎ ‎ 故点M的极坐标为(,) ‎ ‎ (Ⅱ)M点的直角坐标为(),A(l,0)，故直线AM的参数方程为 ‎ (t为参数). ‎ ‎2. (2010年高考宁夏卷文科23)（本小题满分10分）选修4—4：坐标系与参数方程 y=tsina X=1+tcosa y=‎ X=‎ 已知直线：{ {t为参数}。图：{ {为参数}‎ ‎（Ⅰ）当a=时，求与的交点坐标：‎ ‎（Ⅱ）过坐标原点O做的垂线，垂足为A、P为OA的中点，当a变化时，求P点轨迹的参数方程，并指出它是什么曲线。‎ ‎（23）解：‎ ‎（I）当时，C1的普通方程为，‎ C2的普通方程为.‎ 联立方程组解得C1与C2的交点为（1,0），‎ ‎（II）C1的普通方程为.‎ A点坐标为，故当变化时，P点轨迹的参数方程为 ‎ （为参数）‎ P点轨迹的普通方程为 故P点是圆心为，半径为的圆