- 116.00 KB
- 2021-04-16 发布
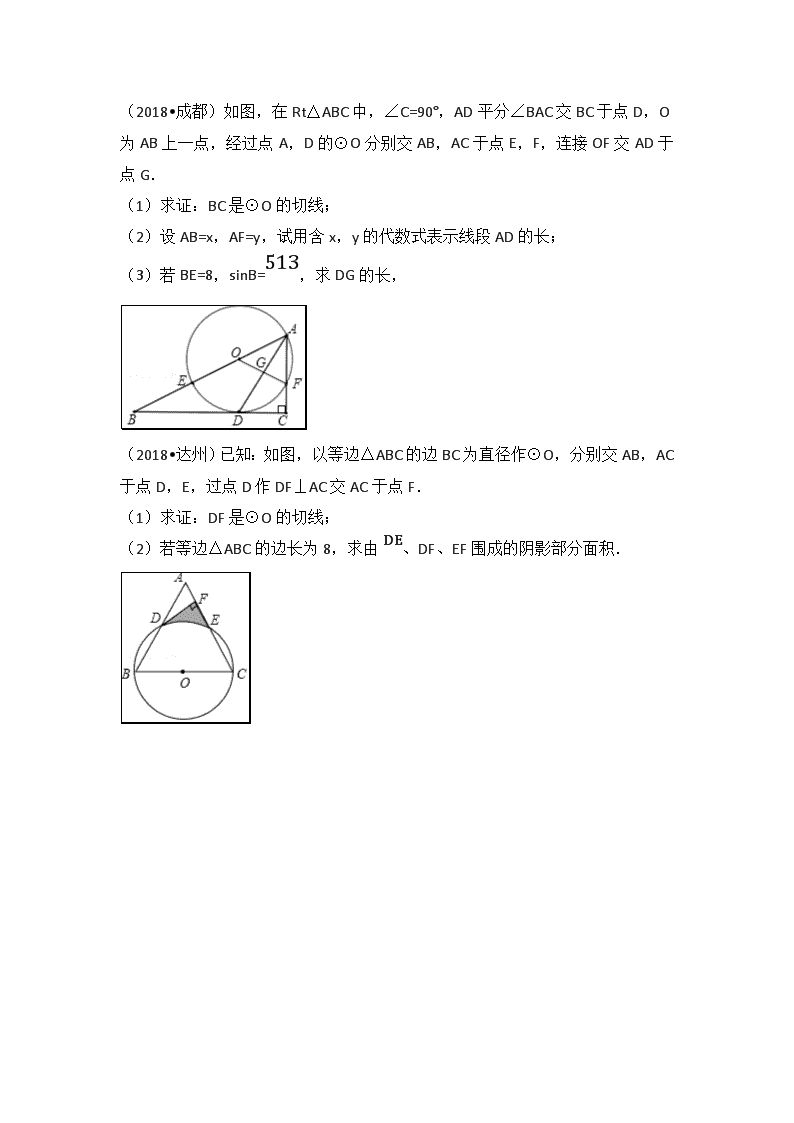
(2018•成都)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=513,求DG的长,
(2018•达州)已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由DE、DF、EF围成的阴影部分面积.
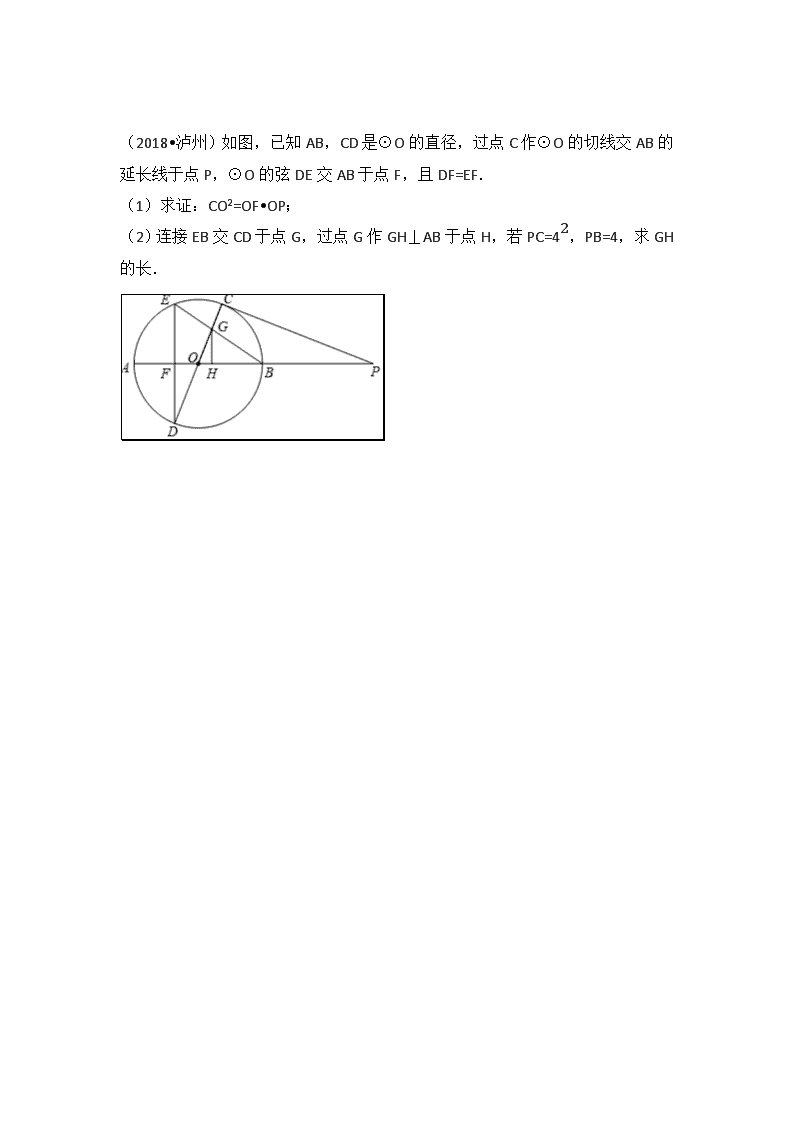
(2018•泸州)如图,已知AB,CD是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,⊙O的弦DE交AB于点F,且DF=EF.
(1)求证:CO2=OF•OP;
(2)连接EB交CD于点G,过点G作GH⊥AB于点H,若PC=42,PB=4,求GH的长.
(2018•达州)阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是A1A2上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:PA1+PA2PA1+PA2+PA3=12是定值.
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M
∴PA3=MA2=PA2+PM=PA2+PA1.
∴PA1+PA2PA1+PA2+PA3=12,是定值.
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4
”,其余条件不变,请问:PA1+PA2PA1+PA2+PA3+PA4还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则PA1+PA2PA1+PA2+PA3+PA4+PA5= (5-1)28 (只写出结果).
您可能关注的文档
相关文档
- 2017-2018学年河北省邯郸市鸡泽县2021-04-16 12:10:247页
- 【生物】西藏拉萨中学2019-2020学2021-04-16 12:10:0610页
- 2018-2019学年安徽省阜阳市第三中2021-04-16 12:09:5710页
- 山东省济宁市2012年中考化学试题2021-04-16 12:09:528页
- 中考数学专题复习练习:一次函数中考2021-04-16 12:09:291页
- 2018-2019学年江西省宜春九中(外国2021-04-16 12:09:2312页
- 中考数学专题复习练习:二次根式教材2021-04-16 12:08:5913页
- 2020年陕西省西安市高新一中中考数2021-04-16 12:08:4512页
- 2019年广东省深圳市光明新区中考数2021-04-16 12:08:4017页
- 中考化学模拟试卷14含解析2021-04-16 12:08:3020页