- 2.76 MB
- 2021-04-16 发布
线面、面面垂直练习题
1、已知:如图,P 是棱形 ABCD 所在平面外一点,且 PA=PC
求证: AC PBD 平面
2、如图,在空间四边形 ABCD 中, AB AC , DB DC 。
求证: BC AD
3、在正方体 1AC 中,M 为棱 1CC 的中点,AC 交 BD 于 O,
求证: 1 AO 平面 BDM。
4、如图,四棱锥 S ABCD 的底面是正方形, SD 平面 ABCD , E 是 SD 的中点.
(Ⅰ)求证: //SB 平面 EAC ;(Ⅱ)求证: AC BE .
A
D
C
B
P
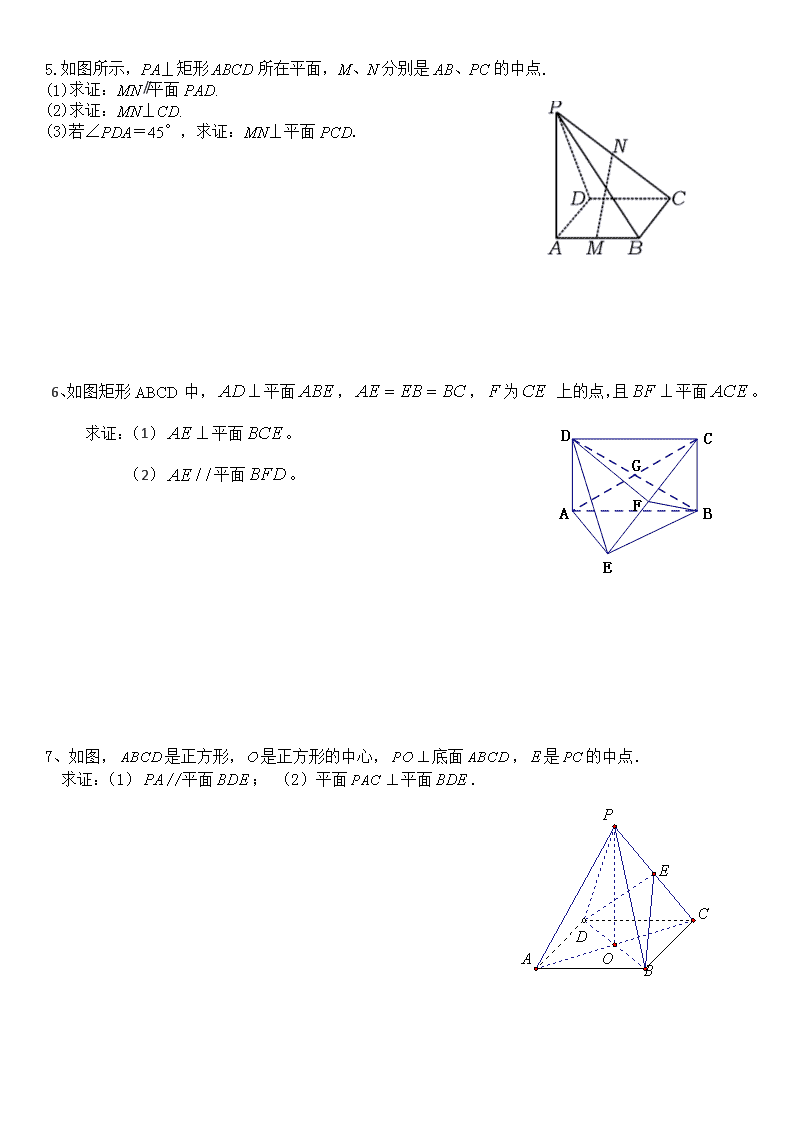
5.如图所示,PA⊥矩形 ABCD 所在平面,M、N 分别是 AB、PC 的中点.
(1)求证:MN∥平面 PAD.
(2)求证:MN⊥CD.
(3)若∠PDA=45°,求证:MN⊥平面 PCD.
6、如图矩形 ABCD 中,AD 平面 ABE ,AE EB BC ,F 为CE 上的点,且 BF 平面 ACE 。
求证:(1) AE 平面 BCE 。
(2) / /AE 平面 BFD 。
7、如图, ABCD 是正方形,O 是正方形的中心, PO 底面 ABCD , E 是 PC 的中点.
求证:(1) PA //平面 BDE ; (2)平面 PAC 平面 BDE .
P
E
D
A B
C
O
A
C
B
D
8、 如图,在三棱锥 BCDA 中,面 ABC 面 BCD , ABC 是正三角形,
90BCD .求证: CDAB ;
9、如图,平行四边形 ABCD 中, CDBD ,正方形 ADEF 所在的平面和平面 ABCD 垂直,H 是 BE 的
中点,G 是 ,AE DF 的交点.
⑴求证: //GH 平面CDE ;
⑵求证: BD 平面CDE .
10、如图,四棱锥 P—ABCD 中,PA⊥平面 ABCD,PA=AB,底面 ABCD 为直角梯形,
∠ABC=∠BAD=90°, ADBCPA 2
1 . 求证:平面 PAC⊥平面 PCD。
11、如图,四棱锥 P—ABCD 的底面是 AB=2,BC= 2 的矩形,侧面 PAB 是等边三角形,且侧面 PAB
⊥底面 ABCD。证明:侧面 PAB⊥侧面 PBC;
12、正方体 1AC 中,求证: 1AC 平面 1C BD
13、如图,正方形 ABCD 的边长是 1,分别取 ,BC CD 的中点 ,E F ,连接 , ,AE EF AF 以 , ,AE EF AF
为折痕,折叠这个正方形,使点 , ,B C D重合于一点 P ,得到一个四面体。
(1)求证: AP EF 。
(2)求证:平面 APE 平面 APF 。
您可能关注的文档
相关文档
- 湖北省荆门市龙泉中学2016届高三文2021-04-15 15:09:225页
- 干货近五年高考历史全国卷考点分布2021-04-14 00:31:325页
- 高三文科主任工作计划2021-04-13 13:47:593页
- 2012年数学高三文科1~4章练习卷 2021-04-12 19:35:175页
- 高三文科线面、面面垂直练习题(供2021-04-12 13:30:514页
- 湖北省荆门市龙泉中学2016届高三文2021-02-27 09:06:105页
- 教学工作总结-高三文科班主任工作2021-02-26 22:32:143页
- 湖北省荆门市龙泉中学2016届高三文2021-02-26 21:11:235页
- 春高三文科综合地理第一次高考模拟2021-02-26 20:09:287页
- 【精品】高三文科班主任工作计划_2021-02-26 19:59:4510页