《同步课时卷》北师版八年级数学（下册）6 6页

‎《同步课时卷》北师版八年级数学（下册）‎ ‎6.2平行四边形的判定（第一课时）‎ ‎1.A,B,C,D四点在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有(　　)‎ A.3种 B.4种 C.5种 D.6种 ‎2.如图6-2-1所示,在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是　‎ ‎　(添加一个条件即可). 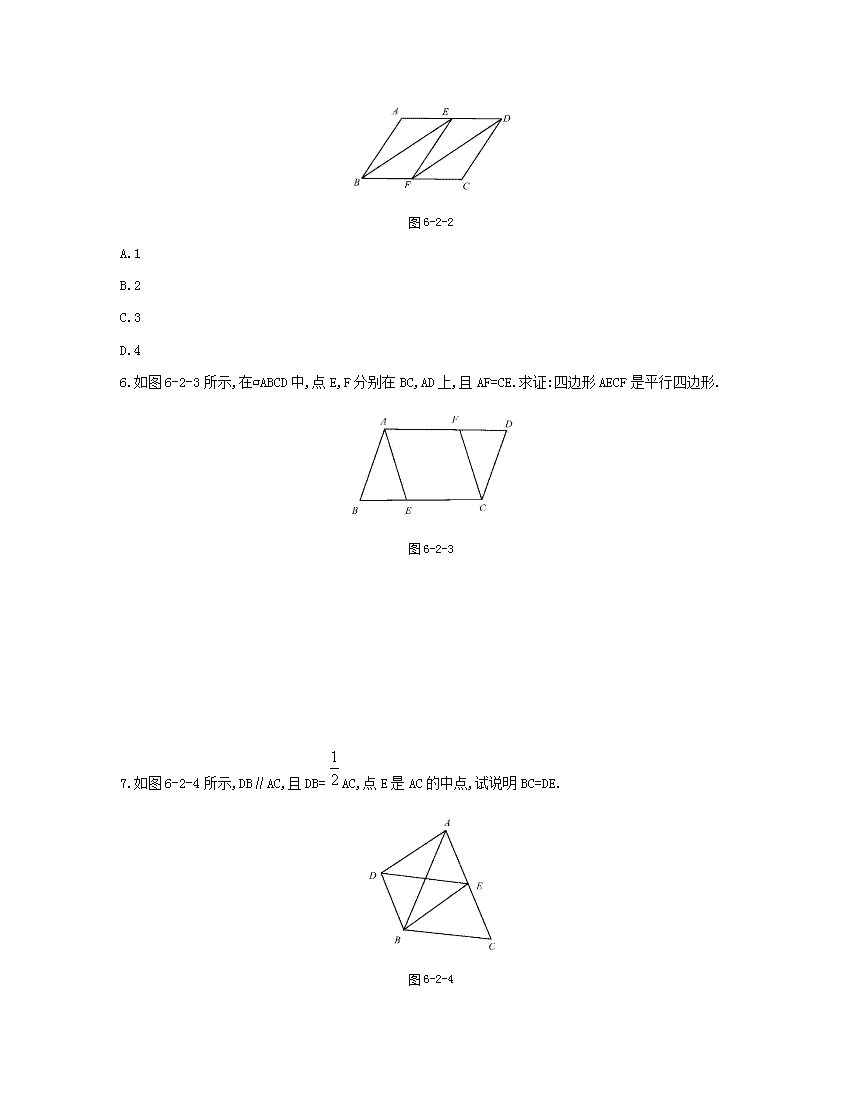‎ 图6-2-1‎ ‎3.在四边形ABCD中,AD∥BC,且AD=BC,若AB=4cm,则DC的长等于(　　)‎ A.2cm B.3cm C.4cm D.5cm ‎4.在四边形ABCD中,AD∥BC,要判定四边形ABCD是平行四边形,那么还需要满足(　　)‎ A.∠A+∠C=180°‎ B.∠B+∠D=180°‎ C.∠A+∠B=180°‎ D.∠A+∠D=180°‎ ‎5.如图6-2-2所示,在平行四边形ABCD中,点E,F分别为边AD,BC的中点,则图中平行四边形的个数是(不包括平行四边形ABCD)(　　)‎ 图6-2-2‎ A.1‎ B.2‎ C.3‎ D.4‎ ‎6.如图6-2-3所示,在▱ABCD中,点E,F分别在BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.‎ 图6-2-3‎ ‎7.如图6-2-4所示,DB∥AC,且DB=AC,点E是AC的中点,试说明BC=DE.‎ 图6-2-4‎ ‎8.下列条件能判定四边形ABCD为平行四边形的是(　　)‎ ‎①AB∥CD,AB=CD;‎ ‎②AB=CD,AD=BC;‎ ‎③AB=CD,AD∥BC;‎ ‎④AB∥CD,AD∥BC.‎ A.①②③‎ B.②③④‎ C.①②④‎ D.①③④‎ ‎9.在四边形ABCD中,AB=CD,BC=AD,若∠A=80°,则∠C=　　. ‎ ‎10.如图6-2-5,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.‎ 求证:四边形BFCE是平行四边形.‎ 图6-2-5‎ ‎11.如图6-2-6所示,点E,F是四边形ABCD的对角线AC上两点,已知DF∥BE,且AF=CE,DF=BE,试说明:‎ ‎(1)△AFD≌△CEB;‎ ‎(2)四边形ABCD是平行四边形.‎ 图6-2-6‎ ‎12.如图6-2-7所示,AC是平行四边形ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足分别为点M,N,四边形BMDN是平行四边形吗?并说明你的理由.‎ 图6-2-7‎ 参考答案 ‎1.B ‎2.AB=CD(答案不唯一)‎ ‎3.C ‎4.D ‎5.C ‎6.证明:∵四边形ABCD是平行四边形,‎ ‎∴AD∥BC,即AF∥CE.‎ 又∵AF=CE,‎ ‎∴四边形AECF是平行四边形.‎ ‎7.证明:∵点E是AC的中点,‎ ‎∴EC=AC.‎ 又∵DB=AC,‎ ‎∴EC=DB.‎ ‎∵DB∥AC,即DB∥EC,‎ ‎∴四边形DBCE是平行四边形.‎ ‎∴BC=DE.‎ ‎8.C ‎9.80°‎ ‎10.证明:∵AB=DC,‎ ‎∴AB+BC=BC+CD,‎ ‎∴AC=DB.‎ 在△AEC和△DFB中,‎ ‎∴△AEC≌△DFB(SAS),‎ ‎∴EC=BF,∠ACE=∠DBF,‎ ‎∴EC∥BF,‎ ‎∴四边形BFCE是平行四边形.‎ ‎11.证明:(1)∵DF∥BE,‎ ‎∴∠DFA=∠BEC.‎ 又∵AF=CE,DF=BE,‎ ‎∴△AFD≌△CEB.‎ ‎(2)由(1)知△AFD≌△CEB,‎ ‎∴∠DAC=∠BCA,AD=BC,‎ ‎∴AD∥BC.‎ ‎∴四边形ABCD是平行四边形.‎ ‎12.解:四边形BMDN是平行四边形.理由如下:‎ ‎∵四边形ABCD是平行四边形,‎ ‎∴AD=BC,AD∥BC,‎ ‎∴∠DAN=∠BCM.‎ 又∵BM⊥AC,DN⊥AC,‎ ‎∴∠DNA=∠BMC=90°,‎ ‎∴△AND≌△CMB,∴DN=BM.‎ 又∵BM⊥AC,DN⊥AC,‎ ‎∴DN∥BM.‎ ‎∴四边形BMDN是平行四边形.‎