2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第2节函数的单调性与最值课件新人教A版 36页

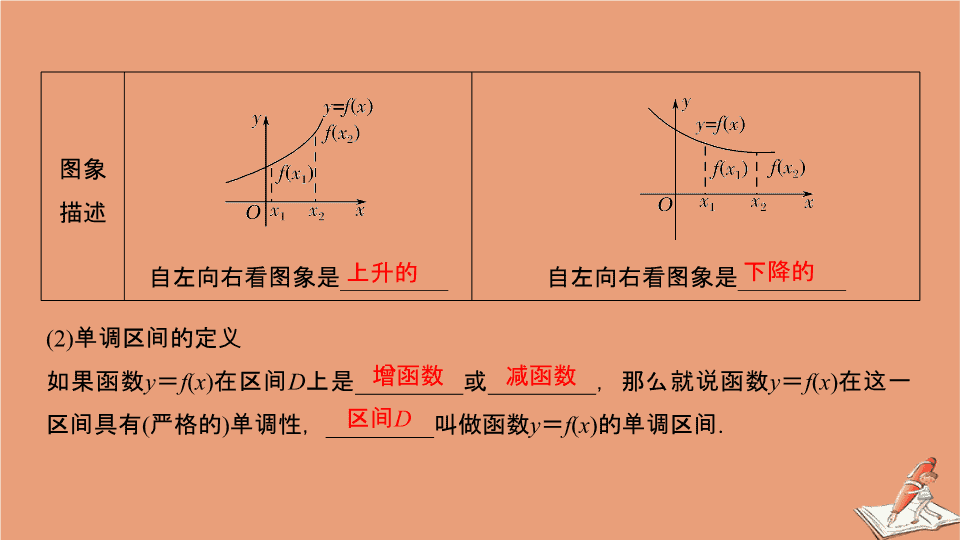
第 2 节　函数的单调性与最值 考试要求　 1. 理解函数的单调性、最大 ( 小 ) 值及其几何意义； 2. 会运用基本初等函数的图象分析函数的性质 . 知 识 梳 理 f ( x 1 )< f ( x 2 ) 1. 函数的单调性 (1) 单调函数的定义   增函数 减函数 定义 一般地，设函数 f ( x ) 的定义域为 I ：如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x 1 ， x 2 当 x 1 < x 2 时，都有 __________ ，那么就说函数 f ( x ) 在区间 D 上是增函数 当 x 1 < x 2 时，都有 __________ ，那么就说函数 f ( x ) 在区间 D 上是减函数 f ( x 1 )> f ( x 2 ) 图象 描述 自左向右看图象是 _________ 自左向右看图象是 _________ 上升的 下降的 (2) 单调区间的定义 如果函数 y ＝ f ( x ) 在区间 D 上是 _________ 或 _________ ，那么就说函数 y ＝ f ( x ) 在这一区间具有 ( 严格的 ) 单调性， _________ 叫做函数 y ＝ f ( x ) 的单调区间 . 增函数 减函数 区间 D 2. 函数的最值 前提 设函数 y ＝ f ( x ) 的定义域为 I ，如果存在实数 M 满足 条件 (1) 对于任意 x ∈ I ，都有 _________ ； (2) 存在 x 0 ∈ I ，使得 f ( x 0 ) ＝ M (3) 对于任意 x ∈ I ，都有 _________ ； (4) 存在 x 0 ∈ I ，使得 _________ 结论 M 为最大值 M 为最小值 f ( x ) ≤ M f ( x ) ≥ M f ( x 0 ) ＝ M [ 常用结论与微点提醒 ] 1. 若 f ( x ) ， g ( x ) 均为区间 A 上的增 ( 减 ) 函数，则 f ( x ) ＋ g ( x ) 也是区间 A 上的增 ( 减 ) 函数 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) 解析 　 (2) 此单调区间不能用并集符号连接，取 x 1 ＝－ 1 ， x 2 ＝ 1 ，则 f ( － 1) ＜ f (1) ，故应说成单调递减区间为 ( － ∞ ， 0) 和 (0 ，＋ ∞ ). (3) 应对任意的 x 1 ＜ x 2 ， f ( x 1 ) ＜ f ( x 2 ) 成立才可以 . (4) 若 f ( x ) ＝ x ， f ( x ) 在 [1 ，＋ ∞ ) 上为增函数，但 y ＝ f ( x ) 的单调递增区间是 R . 答案 　 (1) √ 　 (2) × 　 (3) × 　 (4) × 2. ( 老教材必修 1P39B3 改编 ) 下列函数中，在区间 (0 ，＋ ∞ ) 上单调递增的是 ( 　　 ) 答案　 2 4. (2017· 全国 Ⅱ 卷 ) 函数 f ( x ) ＝ ln( x 2 － 2 x － 8) 的单调递增区间是 ( 　　 ) A.( － ∞ ，－ 2) B.( － ∞ ， 1) C.(1 ，＋ ∞ ) D.(4 ，＋ ∞ ) 解析 　由 x 2 － 2 x － 8>0 ，得 x >4 或 x < － 2. 设 t ＝ x 2 － 2 x － 8 ，则 y ＝ ln t 为增函数 . 要求函数 f ( x ) 的单调递增区间，即求函数 t ＝ x 2 － 2 x － 8 的单调递增区间 . ∵ 函数 t ＝ x 2 － 2 x － 8 的单调递增区间为 (4 ，＋ ∞ ) ， ∴ 函数 f ( x ) 的单调递增区间为 (4 ，＋ ∞ ). 答案 　 D 5. (2020· 新乡模拟 ) 函数 y ＝ f ( x ) 是定义在 [ － 2 ， 2] 上的减函数，且 f ( a ＋ 1)< f (2 a ) ，则实数 a 的取值范围是 ________. 答案　 [ － 1 ， 1) 答案　 2 考点一　确定函数的单调性 ( 区间 ) 答案　 A 由于－ 1< x 1 < x 2 <1 ， 所以 x 2 － x 1 >0 ， x 1 － 1<0 ， x 2 － 1<0 ， 故当 a >0 时， f ( x 1 ) － f ( x 2 )>0 ，即 f ( x 1 )> f ( x 2 ) ，函数 f ( x ) 在 ( － 1 ， 1) 上单调递减； 当 a <0 时， f ( x 1 ) － f ( x 2 )<0 ， 即 f ( x 1 )< f ( x 2 ) ，函数 f ( x ) 在 ( － 1 ， 1) 上单调递增 . 当 a >0 时， f ′( x )<0 ，函数 f ( x ) 在 ( － 1 ， 1) 上单调递减； 当 a <0 时， f ′( x )>0 ，函数 f ( x ) 在 ( － 1 ， 1) 上单调递增 . 规律方法　 1.(1) 求函数的单调区间，应先求定义域，在定义域内求单调区间，如例 1(1).(2) 单调区间不能用集合或不等式表达，且图象不连续的单调区间要用 “ 和 ”“ ， ” 连接 . 2.(1) 函数单调性的判断方法有： ① 定义法； ② 图象法； ③ 利用已知函数的单调性； ④ 导数法 . (2) 函数 y ＝ f [ g ( x )] 的单调性应根据外层函数 y ＝ f ( t ) 和内层函数 t ＝ g ( x ) 的单调性判断，遵循 “ 同增异减 ” 的原则 . 函数的图象如图所示的实线部分，根据图象， g ( x ) 的递减区间是 [0 ， 1). 答案　 [0 ， 1) 解　 f ( x ) 在 [1 ， 2] 上单调递增，证明如下： 考点二　求函数的最值 【例 2 】 (1) 已知函数 f ( x ) ＝ a x ＋ log a x ( a >0 ，且 a ≠ 1) 在 [1 ， 2] 上的最大值与最小值之和为 log a 2 ＋ 6 ，则 a 的值为 ( 　　 ) 解析　 (1) f ( x ) ＝ a x ＋ log a x 在 [1 ， 2] 上是单调函数， 所以 f (1) ＋ f (2) ＝ log a 2 ＋ 6 ， 则 a ＋ log a 1 ＋ a 2 ＋ log a 2 ＝ log a 2 ＋ 6 ， 即 ( a － 2)( a ＋ 3) ＝ 0 ，又 a >0 ，所以 a ＝ 2. (2) 法一 　在同一坐标系中，作函数 f ( x ) ， g ( x ) 的图象， 依题意， h ( x ) 的图象如图所示的实线部分 . 易知点 A (2 ， 1) 为图象的最高点， 因此 h ( x ) 的最大值为 h (2) ＝ 1. 当 0< x ≤ 2 时， h ( x ) ＝ log 2 x 是增函数， 当 x >2 时， h ( x ) ＝ 3 － x 是减函数， 因此 h ( x ) 在 x ＝ 2 时取得最大值 h (2) ＝ 1. 答案　 (1)C 　 (2)1 规律方法　 求函数最值的四种常用方法 (1) 单调性法：先确定函数的单调性，再由单调性求最值 . (2) 图象法：先作出函数的图象，再观察其最高点、最低点，求出最值 . (3) 基本不等式法：先对解析式变形，使之具备 “ 一正二定三相等 ” 的条件后用基本不等式求出最值 . (4) 导数法：先求导，然后求出在给定区间上的极值，最后结合端点值，求出最值 . 【训练 2 】 (1) 定义 max{ a ， b ， c } 为 a ， b ， c 中的最大值，设 M ＝ max{2 x ， 2 x － 3 ， 6 － x } ，则 M 的最小值是 ( 　　 ) 解析　 (1) 画出函数 M ＝ {2 x ， 2 x － 3 ， 6 － x } 的图象 ( 如图 ) ，由图可知，函数 M 在 A (2 ， 4) 处取得最小值 2 2 ＝ 6 － 2 ＝ 4 ，故 M 的最小值为 4. 考点三　函数单调性的应用　 多维探究 角度 1 　利用单调性比较大小 A. c > a > b B. c > b > a C. a > c > b D. b > a > c 答案　 D 角度 2 　求解函数不等式 A.( － ∞ ，－ 1] B.(0 ，＋ ∞ ) C.( － 1 ， 0) D.( － ∞ ， 0) 答案　 D 角度 3 　求参数的值或取值范围 【例 3 － 3 】 (1) (2018· 全国 Ⅱ 卷 ) 若 f ( x ) ＝ cos x － sin x 在 [0 ， a ] 上是减函数，则 a 的最大值是 ( 　　 ) 规律方法　 1. 比较函数值的大小，应将自变量转化到同一个单调区间内，然后利用函数的单调性解决 . 2. 求解函数不等式，其实质是函数单调性的逆用，由条件脱去 “ f ” . 3. 利用单调性求参数的取值 ( 范围 ) 的思路是：根据其单调性直接构建参数满足的方程 ( 组 )( 不等式 ( 组 )) 或先得到其图象的升降，再结合图象求解 . 对于分段函数，要注意衔接点的取值 . 解析 　 (1) 作出函数 f ( x ) 的图象如图所示，知函数 f ( x ) 在 R 上是减函数， (2) 因为 f ( x ) 是定义域为 R 的偶函数， 答案　 (1)A 　 (2)C 　 (3)D