2019届高考数学（理）倒计时模拟卷（3） 14页

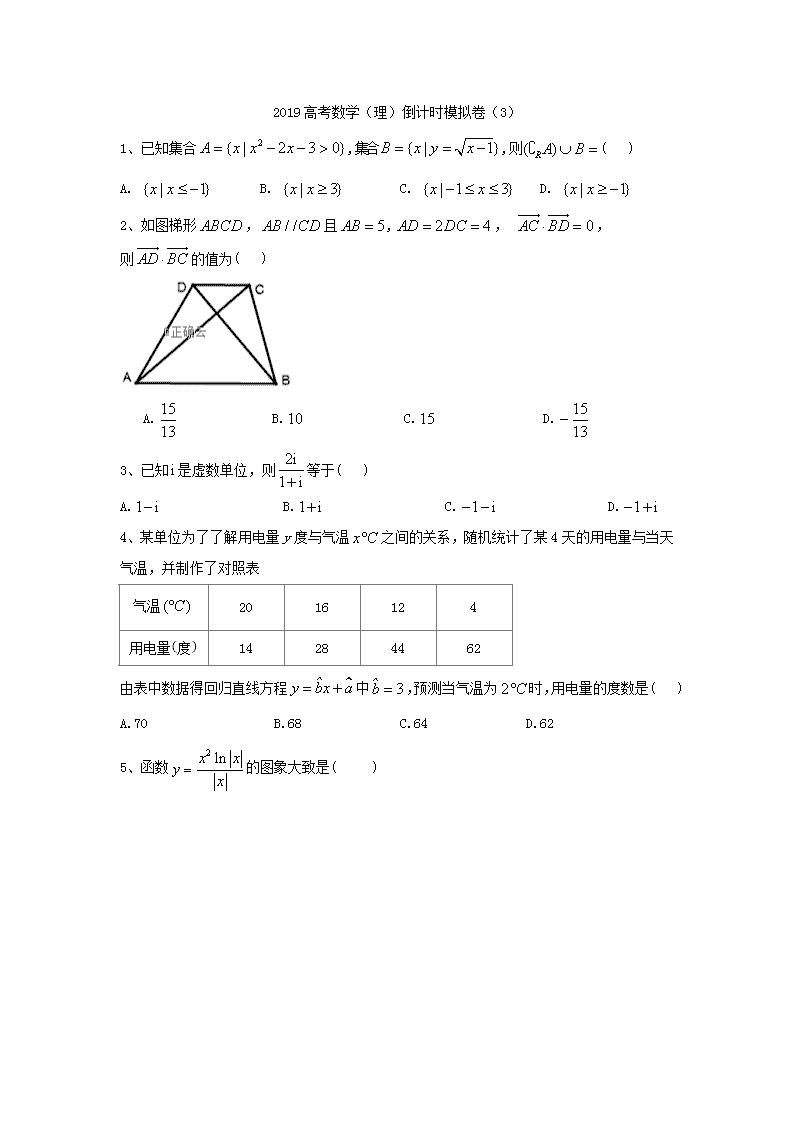
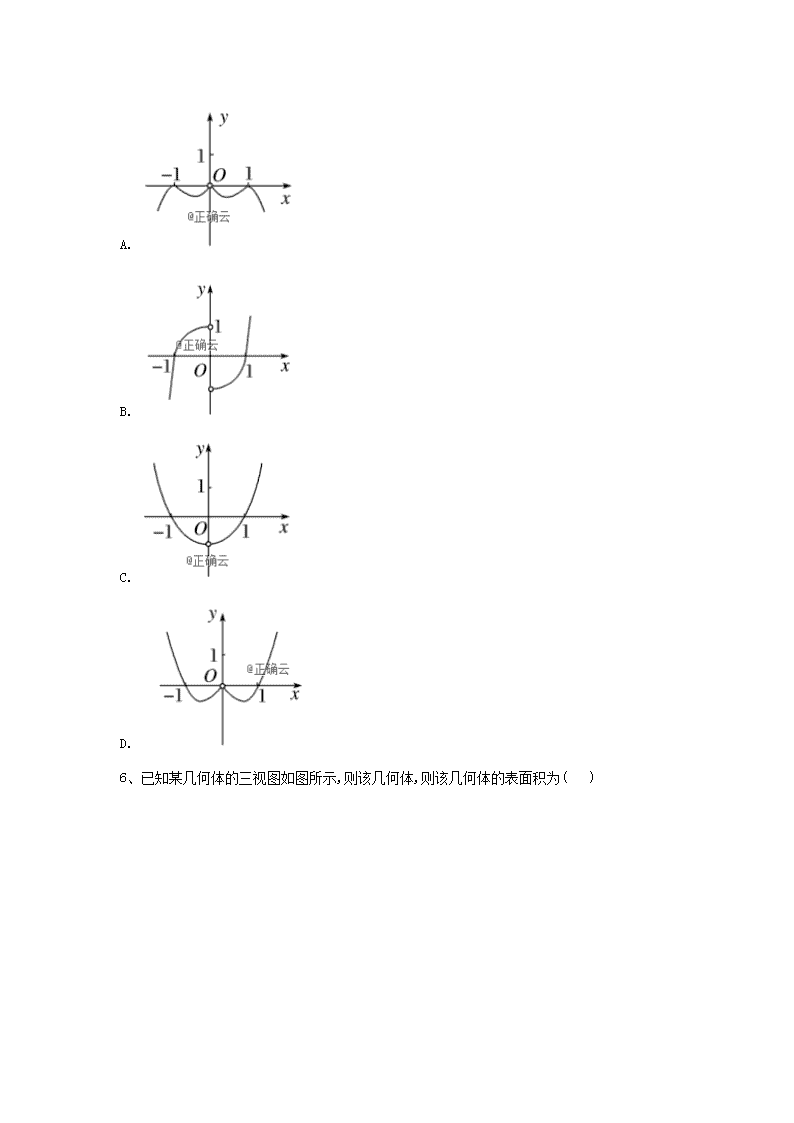
‎2019高考数学（理）倒计时模拟卷（3）‎ ‎1、已知集合,集合,则( ) A. B. C. D. ‎ ‎2、如图梯形，且,， ，‎ 则的值为( )‎ A. B. C. D.‎ ‎3、已知是虚数单位，则等于( )‎ A. B. C. D. ‎ ‎4、某单位为了了解用电量y度与气温之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表 气温 ‎20‎ ‎16‎ ‎12‎ ‎4‎ 用电量度 ‎14‎ ‎28‎ ‎44‎ ‎62‎ 由表中数据得回归直线方程中，预测当气温为时，用电量的度数是( )‎ A.70 B.68 C.64 D.62‎ ‎5、函数的图象大致是(   )‎ A. B. C. D.‎ ‎6、已知某几何体的三视图如图所示,则该几何体,则该几何体的表面积为( )‎ ‎ A. B. C. D. ‎ ‎7、若,那么的值为(   )‎ A. B. C. D. ‎ ‎8、记为数列的前n项和,若,则( ) A.40 B.80 C.121 D.242‎ ‎9、已知是空间中的两条不同的直线, 是空间中的两个不同的平面,则下列命题正确的是(   )‎ A.若,则. B.若,则. C.若,则. D.若,则.‎ ‎10、已知直线与抛物线相切，则双曲线：的离心率等于( )‎ A. B. C. D.‎ ‎11、如图，函数的图象是由正弦曲线或余弦曲线经过变换得到的，则的解析式可以是(   ) A． B． C． D．‎ ‎12、若曲线和上分别存在点,使得△是以原点为直角顶点的直角三角形, 交轴于点,且,则实数的取值范围是(   )‎ A. B. C. D. ‎ ‎13、的展开式中的系数是,则__________‎ ‎14、直线与圆相交于两点，若，则____．‎ ‎15、已知实数满足不等式组，则的最小值为_________‎ ‎16、已知直线与抛物线交于两点,过线段的中点作轴的垂线,交抛物线于点,若,则__________‎ ‎17、在中,内角所对的边分别为,且.‎ ‎(1)求的值；‎ ‎(2)若，的面积为，求的值．‎ ‎18、如图,五边形中,四边形为长方形,△为边长为的正三角形,将△沿折起,使得点在平面上的射影恰好在上.‎ ‎1.当时,证明:平面平面;‎ ‎2.若,求平面与平面所成二面角的余弦值的绝对值.‎ ‎19、手机中的“运动”具有这样的功能,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数.小明的朋友圈里有大量好友参与了“运动”,他随机选取了其中名,其中男女各名,记录了他们某一天的走路步数,统计数据如表所示:‎ 男 ‎0‎ ‎2‎ ‎4‎ ‎7‎ ‎2‎ 女 ‎1‎ ‎3‎ ‎7‎ ‎3‎ ‎1‎ ‎1.以样本估计总体,视样本频率为概率,在小明朋友圈里的男性好友中任意选取名,其中走路步数低于步的有名,求的分布列和数学期望 ‎2.如果某人一天的走路步数超过步,此人将被“运动”评定为“积极型”,否则为“消极型”.根据题意完成下面的列联表,并据此判断能否有以上的把握认为“评定类型”与“性别”有关?‎ 积极型 消极型 总计 男 女 总计 附: ‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.01‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎20、如图,在平面直角坐标系中,已知点,过直线左侧的动点作于点,的角平分线交轴于点,且,记动点的轨迹为曲线.‎ ‎1.求曲线的方程 ‎2.过点作直线交曲线于两点,设,若,求的取值范围 ‎21、设函数,.‎ ‎1.求函数的单调区间;‎ ‎2.当时,求函数的极值.‎ ‎22、在平面角坐标系中,已知椭圆的方程为动点在椭圆上, 为原点,线段的中点为.‎ ‎1.以为极点, 轴的正半轴为极轴,建立极坐标系,求点的轨迹的极坐标方程;‎ ‎2.设直线的参数方程为 (为参数), 与点的轨迹交于两点,求弦长.‎ ‎23、[选修4—5:不等式选讲]‎ 已知函数.‎ ‎1.求的解集; ‎ ‎2.若关于的不等式能成立,求实数的取值范围.‎ 答案 ‎1.C 解析：由题意得, ,所以,故选C.‎ ‎2.B ‎3.B 解析：，‎ 故选：B ‎4.A ‎5.D ‎6.D 解析：根据该几何体的三视图可知,该几何体为如图所示的四棱锥,其表面积 ‎.‎ ‎7.D ‎8.C 解析：由,,得,所以,由,得,所以数列是以1为首项,3为公比的等比数列,所以,故选C.‎ ‎9.D ‎10.B 解析：由得，因为直线与曲线相切，所以，，所以双曲线为，离心率等于，故选B.‎ ‎11.A ‎12.D ‎13.-1‎ 解析：展开式中的系数是,所以,所以.‎ ‎14.‎ ‎15.1‎ 解析：画出不等式组表示的平面区域，如图中阴影部分所示； 由，解得， 设，将直线进行平移， 当经过点B时，目标函数z达到最小值，‎ ‎． 故答案为：1． ‎ ‎16.2‎ 解析：由得 设 则 设的中点为则,‎ 由可得 即,即,又知是线段的中点 ‎∴∵轴 ‎∴‎ 又 ‎∴‎ 所以此时满足成立故 ‎17.(1)原等式化简得，‎ ‎∴，‎ ‎∴，‎ ‎∵，，∴.‎ ‎(2)∵，且，∴为锐角，且，‎ ‎∴，，∵，∴.‎ 由余弦定理得：.‎ ‎18.1.作,垂足为,依题意得平面,‎ ‎,又,‎ 平面,.‎ 利用勾股定理得,‎ 同理可得.‎ 在△中, ‎ 平面,又平面,‎ 所以平面平面. 2.连接,,,‎ ‎,又四边形为长方形, .‎ 取中点为,得,连结,‎ 其中,,‎ 由以上证明可知互相垂直,‎ 不妨以为轴建立空间直角坐标系.‎ ‎ ,,‎ 设是平面的法向量,‎ 则有即,‎ 令得.‎ 设是平面的法向量,‎ 则有即 令得.‎ 则 所以平面与平面所成二面角的余弦值的绝对值为.‎ ‎19.1.在小明的男性好友中任意选取名,其中走路步数低于的概率为.可能取值分别为,,‎ ‎,‎ ‎,‎ ‎,‎ 积极型 消极型 总计 男 ‎9‎ ‎6‎ ‎15‎ 女 ‎4‎ ‎11‎ ‎15‎ 总计 ‎13‎ ‎17‎ ‎30‎ 的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 则 2.完成列联表 的观测值.‎ 据此判断没有以上的把握认为“评定类型”与“性别”有关 ‎20.1.设,由题可知,所以,即,化简整理得,‎ 即曲线的方程为. 2.由题意,直线的斜率,设直线的方程为,‎ 由得,‎ 设,所以△恒成立,‎ 且,①又因为,所以,②‎ 联立①②,消去,得 因为,所以,解得.‎ 又,,‎ 因为,所以.‎ 所以的取值范围是.‎ 解析：点睛:本题主要考查了求轨迹方程、直线与椭圆的位置关系等,考查推理论证能力、运算求解能力,方程与函数思想,数形结合思想等,属于中档题。‎ ‎21.1. 的减区间,的增区间. 2. 时, 无极值,‎ 时, ,.‎ ‎ ‎ ‎22.1.点轨迹的极坐标方程为 2. ‎ ‎23.1. ‎ 故的解集为 2.由,能成立,‎ 得能成立,即能成立,令,则能成立,‎ 由1知, ‎ 又∵‎ ‎∴‎ ‎∴实数的取值范围:   ‎