2018-2019学年新疆生产建设兵团第一师高级中学高二上学期第二次月考数学（文）试题 Word版 9页

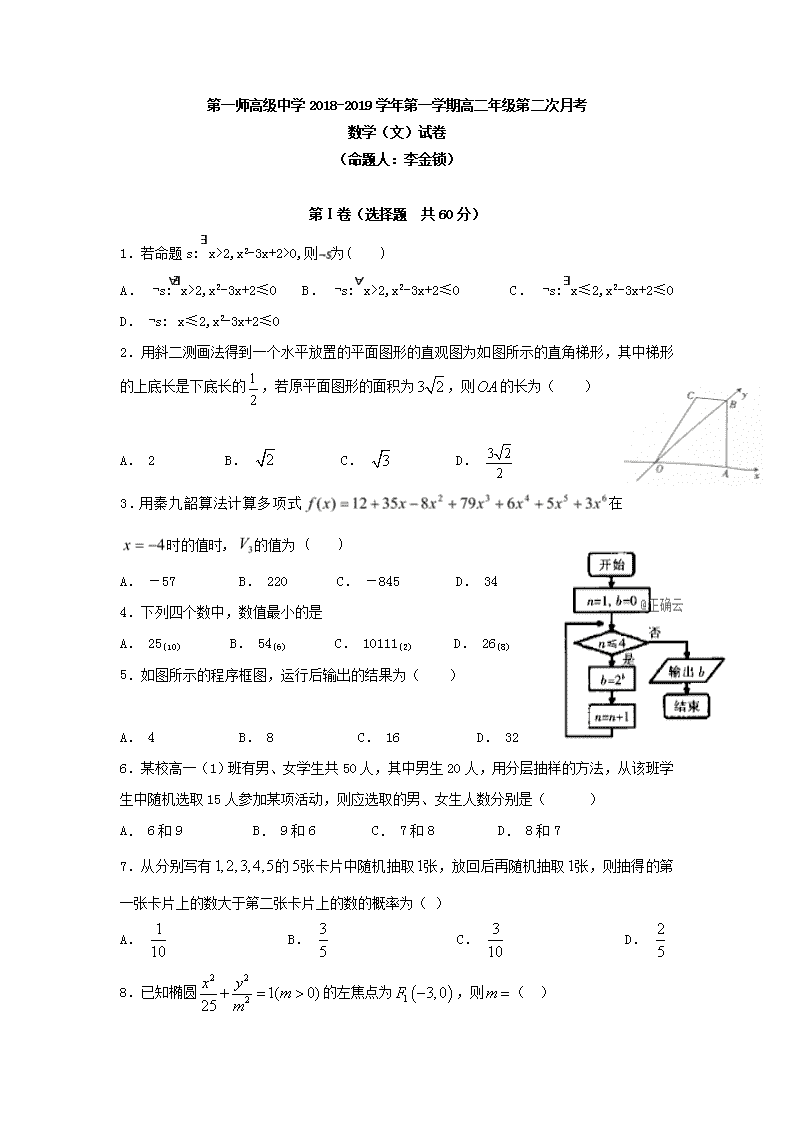
第一师高级中学2018-2019学年第一学期高二年级第二次月考 数学（文）试卷 ‎（命题人：李金锁）‎ 第Ⅰ卷（选择题 共60分）‎ ‎1．若命题s:∃x>2,x2-3x+2>0,则为(　　)‎ A． ¬s:∃x>2,x2-3x+2≤0 B． ¬s:∀x>2,x2-3x+2≤0 C． ¬s:∃x≤2,x2-3x+2≤0 D． ¬s:∀x≤2,x2-3x+2≤0‎ ‎2．用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形，其中梯形的上底长是下底长的，若原平面图形的面积为，则的长为（ ）‎ A． 2 B． C． D． ‎ ‎3．用秦九韶算法计算多项式在时的值时, 的值为 ( )‎ A． －57 B． 220 C． －845 D． 34‎ ‎4．下列四个数中，数值最小的是 A． 25(10) B． 54(6) C． 10111(2) D． 26(8)‎ ‎5．如图所示的程序框图，运行后输出的结果为（ ）‎ A． 4 B． 8 C． 16 D． 32‎ ‎6．某校高一（1）班有男、女学生共50人，其中男生20人，用分层抽样的方法，从该班学生中随机选取15人参加某项活动，则应选取的男、女生人数分别是（ ）‎ A． 6和9 B． 9和6 C． 7和8 D． 8和7 ‎ ‎7．从分别写有的张卡片中随机抽取张，放回后再随机抽取张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为（ ）‎ A． B． C． D． ‎ ‎8．已知椭圆的左焦点为，则（ ）‎ A． 16 B． 9 C． 4 D． 3‎ ‎9．在区间[-2,3]上随机取一个数x，则满足|x-1|≤1的概率是（ ）‎ A． B． C． D． ‎ ‎10．已知某三棱锥的三视图如图所示，则该三棱锥的表面积为（ ）‎ A． B． C． D． ‎ ‎11．已知为两条直线， 为两个不同的平面，则下列说法正确的是（ ）‎ A． 若，则 B． 若，则 C． 若，则 D． 若，则 ‎12．在8件同类产品中，有5件正品，3件次品，从中任意抽取4件，下列事件中的必然事件是（　　）‎ A． 4件都是正品 B． 至少有一件次品 C． 4件都是次品 D． 至少有一件正品 第II卷（共90分）‎ 填空题（每小题5分，共20分）‎ ‎13．已知，，若q是p的必要不充分条件，则实数的取值范围是_____________．‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.5‎ ‎3‎ ‎4‎ ‎14．某企业节能降耗技术改造后，在生产某产品过程中记录的产量（吨）与相应的生产能耗（吨）的几组对应数据如下表所示：‎ 若根据表中数据得出关于的线性回归方程为，则表中的值为_________________.‎ ‎15．已知正三棱柱底面边长是2，该三棱柱的体积为，则该正三棱柱外接球的表面积是_ ．‎ ‎16．若椭圆上一点到两个焦点的距离之和为，则此椭圆的离心率为__________．‎ 解答题（每题12分，第22题10分，共70分）‎ ‎17．设命题实数满足，其中，命题实数满足．‎ ‎（1）若，且为真，求实数的取值范围；‎ ‎（2）若是的充分不必要条件，求实数的取值范围．‎ ‎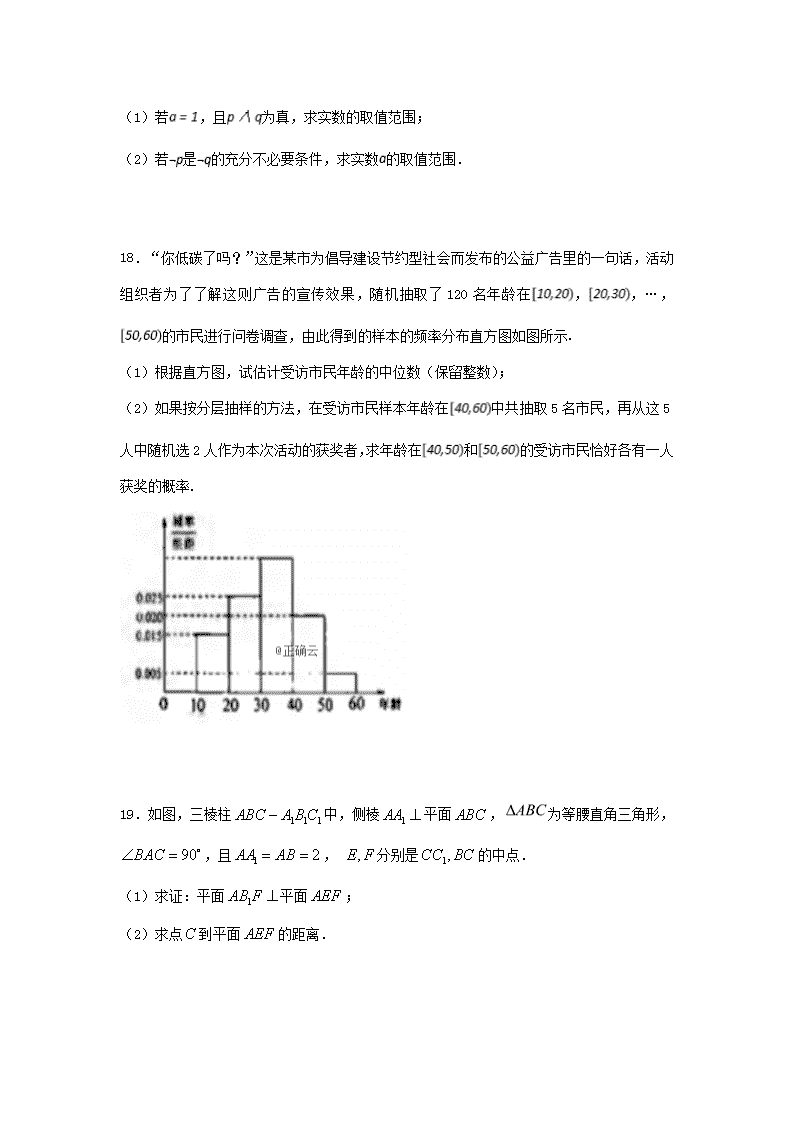18．“你低碳了吗？”这是某市为倡导建设节约型社会而发布的公益广告里的一句话，活动组织者为了了解这则广告的宣传效果，随机抽取了120名年龄在，，…，的市民进行问卷调查，由此得到的样本的频率分布直方图如图所示.‎ ‎（1）根据直方图，试估计受访市民年龄的中位数（保留整数）；‎ ‎（2）如果按分层抽样的方法，在受访市民样本年龄在中共抽取5名市民，再从这5人中随机选2人作为本次活动的获奖者，求年龄在和的受访市民恰好各有一人获奖的概率.‎ ‎19．如图，三棱柱中，侧棱平面，为等腰直角三角形， ，且， 分别是的中点．‎ ‎（1）求证：平面平面；‎ ‎（2）求点到平面的距离．‎ ‎20．四棱锥中，侧面是边长为的正三角形，且与底面垂直，底面是面积为的菱形，为锐角，为的中点．‎ ‎（Ⅰ）求证：面．‎ ‎（Ⅱ）求证： ．‎ ‎（Ⅲ）求三棱锥的体积．‎ ‎21．已知椭圆的左、右焦点分别为，离心率，过且与轴垂直的直线与椭圆在第一象限内的交点为，且.‎ ‎(1)求椭圆的方程；‎ ‎(2)过点的直线交椭圆于两点，当时，求直线的方程.‎ ‎22．已知a∈R，命题p：“∀x∈[1，2]，x2﹣a≥0”，命题q：“∃x∈R，x2+2ax+2﹣a=0”．‎ ‎（1）若命题p为真命题，求实数a的取值范围；‎ ‎（2）若命题“p∨q”为真命题，命题“p∧q”为假命题，求实数a的取值范围．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B A D C A D C B B D B 高二数学文科第二次月考答案卷 ‎13． 14. 15. 16.‎ ‎17．（1）；（2）‎ 解析:（1）当时，由，得． ‎ 由，得，所以． ‎ 由p∧q为真，即p，q均为真命题，因此的取值范围是． ‎ ‎（2）若￢p是￢q的充分不必要条件，可得q是p的充分不必要条件， ‎ ‎ 由题意可得，, ‎ ‎ 所以，因此且，解得．‎ ‎18.解析：（1）受访市民年龄的中位数为：‎ ‎ （岁）.‎ ‎（2）样本年龄在中的有24人，在中的有6人，则按分层抽样的受访市民年龄在中有人，分别记为，，，，在中的有人，记为，‎ 从已抽取的5人中任选2人的所有可能为，，，，，，，，，，共10种，记“年龄在和的受访市民恰好各有一人获奖”为事件A，则事件A包括，，，‎ 共4种，故年龄在和的受访市民恰好各有一人的概率为.‎ ‎19.试题解析：‎ ‎（1）证明： 是等腰直角三角形斜边的中点，‎ ‎∴． 又∵侧棱，∴面面∴ 面， .，则 ，‎ ‎∴，∴．‎ 又，∴⊥平面．…而面，故：平面平面．‎ ‎（2）解：∵⊥，侧棱 所以，所 ‎ 又,,‎ 设点到平面的距离为， ‎ 解得： ‎ ‎20.详解：（Ⅰ）证明：连结交于，则是中点，‎ ‎∵在中，是的中点，是的中点，∴，又平面，平面，∴平面．‎ ‎（Ⅱ）证明：作，则为中点，连结，‎ ‎∵底面是菱形，边长为，面积为，‎ ‎∴，∴，，‎ ‎∴是等边三角形，∴，又∵，∴平面，∴．‎ ‎（Ⅲ）．‎ ‎21.试题解析：‎ ‎(1)设， ，则，∵，∴.①‎ ‎∵，∴.②联立①②得， ， ， .‎ ‎∴椭圆方程为.‎ ‎(2)显然直线斜率存在，设直线方程为： ， 点坐标为， 点坐标为.联立方程组，得，‎ 令得， ，∴， ，‎ 由弦长公式得， ‎ ‎，‎ 点到直线的距离，‎ ‎，解得.‎ ‎∴的方程为： .‎ ‎22.详解：（1）∵命题p：“∀x∈[1，2]，x2﹣a≥0”，令f（x）=x2﹣a，‎ 根据题意，只要x∈[1，2]时，f（x）min≥0即可，‎ 也就是1﹣a≥0，解得a≤1，∴实数a的取值范围是（﹣∞，1]； ‎ ‎（2）由（1）可知，当命题p为真命题时，a≤1，‎ 命题q为真命题时，△=4a2﹣4（2﹣a）≥0，解得a≤﹣2或a≥1．‎ ‎∵命题“p∨q”为真命题，命题“p∧q”为假命题，‎ ‎∴命题p与命题q必然一真一假，‎ 当命题p为真，命题q为假时，，‎ 当命题p为假，命题q为真时，，‎ 综上：a＞1或﹣2＜a＜1．‎