人教新课标A版高一数学1-3实习作业） 1页

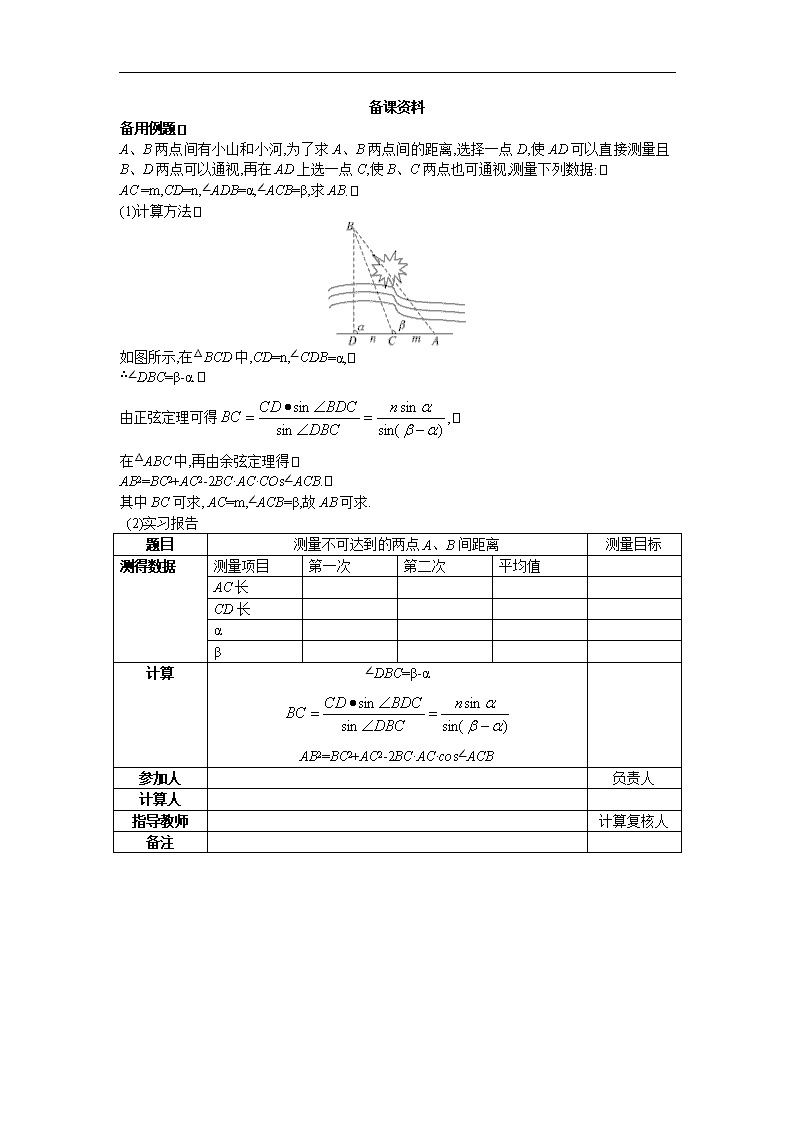
备课资料 备用例题 A、B 两点间有小山和小河,为了求 A、B 两点间的距离,选择一点 D,使 AD 可以直接测量且 B、 D 两点可以通视,再在 AD 上选一点 C,使 B、C 两点也可通视,测量下列数据: AC =m,CD=n,∠ADB=α,∠ACB=β,求 AB. (1)计算方法 如图所示,在△BCD 中,CD=n,∠CDB=α, ∴∠DBC=β-α. 由正弦定理可得 )sin( sin sin sin     n DBC BDCCDBC , 在△ABC 中,再由余弦定理得 AB2=BC2+AC2-2BC·AC·COs∠ACB. 其中 BC 可求, AC=m,∠ACB=β,故 AB 可求. (2)实习报告 题目 测量不可达到的两点 A、B 间距离 测量目标 测得数据 测量项目 第一次 第二次 平均值 AC 长 CD 长 α β 计算 ∠DBC=β-α )sin( sin sin sin     n DBC BDCCDBC AB2=BC2+AC2-2BC·AC·cos∠ACB 参加人 负责人 计算人 指导教师 计算复核人 备注