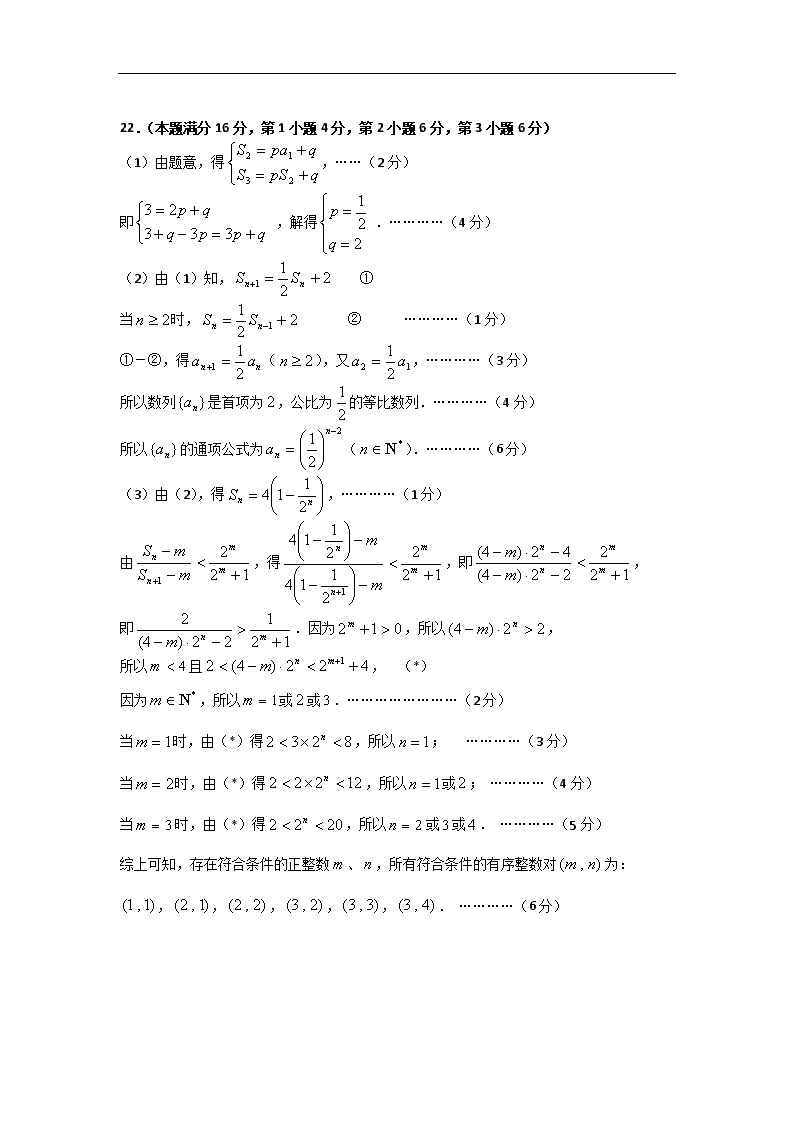- 439.00 KB
- 2024-03-29 发布
上海市嘉定区2013届高三一模数学试题(理科)
参考答案与评分标准
一.填空题(每小题4分,满分56分)
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12.
13. 14.
二.选择题(每小题5分,满分20分)
15.A 16.C 17.B 18.D
三.解答题
19.(本题满分12分)
方程的根为.………………(3分)
因为在复平面内对应的点在第一象限,所以,………………(5分)
所以,解得,因为,所以,……(8分)
所以,所以,故.…………(11分)
所以,.…………(12分)
G
P
A
B
C
F
E
20.(本题满分14分,第1小题8分,第2小题6分)
(1)取中点,中点,中点,
连结,,,则∥,∥,
所以就是异面直线与所成的角(或
其补角).…………(2分)
连结,则,……(3分)
, …………(4分)
又,所以.…………(5分)
在△中,,……(7分)
故.所以异面直线与所成角的大小为.…………(8分)
(2)因为底面,所以,,,
又,所以平面,所以,…………(2分)
所以△、△、△、△都是直角三角形.……(3分)
所以,.……(6分)
21.(本题满分14分,第1小题6分,第2小题8分)
O
A
B
M
x
y
(1)将与代入椭圆的方程,得
,…………(2分)
解得,.…………(5分)
所以椭圆的方程为.…………(6分)
(2)由,知在线段的垂直平分线上,
由椭圆的对称性知、关于原点对称.
①若点、在椭圆的短轴顶点上,则点在椭圆的长轴顶点上,此时
.……(1分)
同理,若点、在椭圆的长轴顶点上,则点在椭圆的短轴顶点上,此时
.……(2分)
②若点、、不是椭圆的顶点,设直线的方程为(),
则直线的方程为.设,,
由,解得,,……(4分)
所以,同理可得,
所以.……(7分)
综上,为定值.…………(8分)
22.(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
(1)由题意,得,……(2分)
即 ,解得 .…………(4分)
(2)由(1)知, ①
当时, ② …………(1分)
①-②,得(),又,…………(3分)
所以数列是首项为,公比为的等比数列.…………(4分)
所以的通项公式为().…………(6分)
(3)由(2),得,…………(1分)
由,得,即,
即.因为,所以,
所以且, (*)
因为,所以或或.……………………(2分)
当时,由(*)得,所以; …………(3分)
当时,由(*)得,所以或; …………(4分)
当时,由(*)得,所以或或. …………(5分)
综上可知,存在符合条件的正整数、,所有符合条件的有序整数对为:
,,,,,. …………(6分)
23.(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
(1)当,时,…(2分)
作函数图像(图像略),可知函数在区间上是增函数,所以的最大值为.…………(4分)
O
a
y
x
(2)……(1分)
①当时,,
因为,所以,
所以在上单调递增.…………(3分)
②当时,,
因为,所以,所以在上单调递增,在上单调递减.…………(5分)
综上,函数的单调递增区间是和,
单调递减区间是.………………(6分)
(3)①当时,,,所以在上是增函数,关于的方程不可能有三个不相等的实数解.…………(2分)
②当时,由(1)知在和上分别是增函数,在上是减函数,当且仅当时,方程有三个不相等的实数解.
即.…………(5分)
令,在时是增函数,故.…………(7分)
所以,实数的取值范围是.…………(8分)