2019-2020学年安徽省定远县育才学校高二（实验班）上学期第三次月考数学（文）试题 word版 10页

定远育才学校2019—2020学年度第一学期第三次月考 高二实验班文科数学 ‎ （本卷满分：150分，时间：120分钟） ‎ ‎ ‎ 一、选择题(共12小题,每小题5分,共60分。) ‎ ‎1.若表示直线，表示平面，且 ， 则“”是“”的（ ）‎ A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎2.直线l1：3kx＋(2－k)y－3＝0和l2：(k－2)x＋(k＋2)y－2＝0互相垂直，则实数k的值是(　　)‎ A. －2或－1 B. 2或1 C. －2或1 D. 2或－1‎ ‎3.一个几何体的三视图如图所示，其中俯视图是菱形，则该几何体的侧面积为（ ）‎ A. B. C. D.‎ ‎4.已知一个圆柱的底面半径和高分别为和，，侧面展开图是一个长方形，这个长方形的长是宽的2倍，则该圆柱的表面积与侧面积的比是（ ）‎ A. B. C. D. ‎ ‎5.曲线与直线有两个交点,则实数的取值范围（ ）.‎ A. B. C. D. 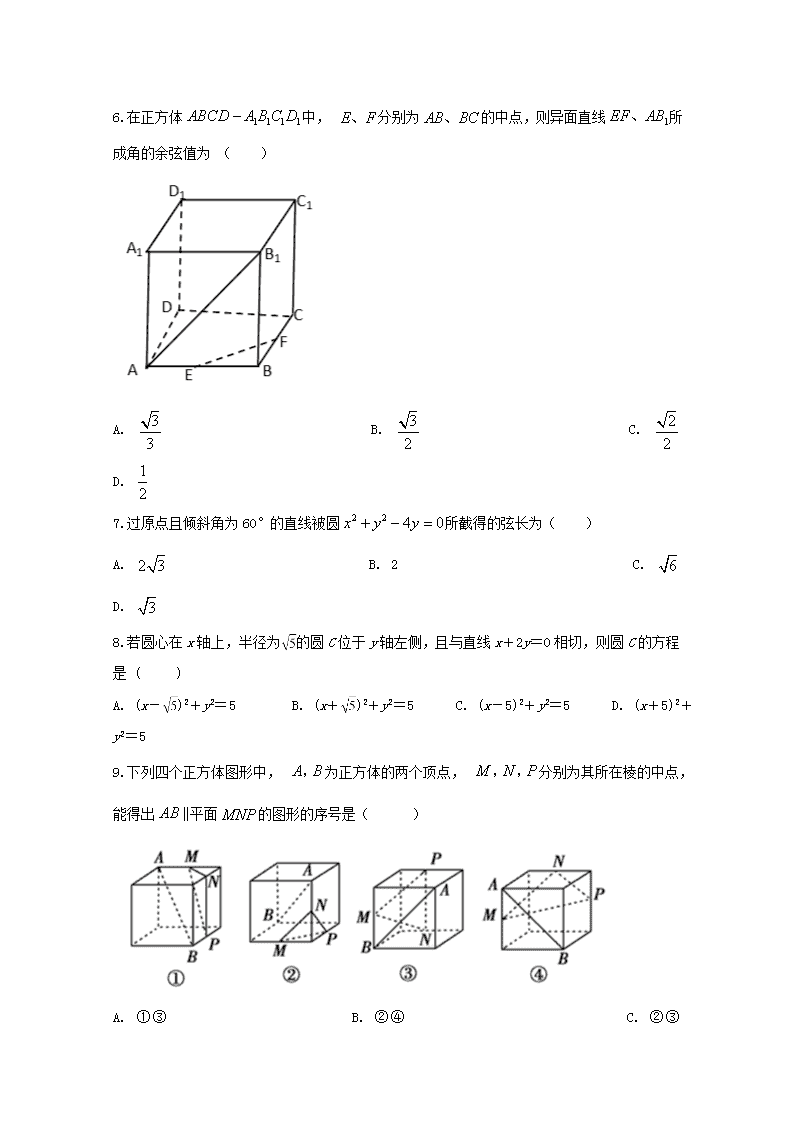‎ ‎6.在正方体中， 分别为的中点，则异面直线所成角的余弦值为 （ ）‎ A. B. C. D. ‎ ‎7.过原点且倾斜角为60°的直线被圆所截得的弦长为（ ）‎ A. B. 2 C. D. ‎ ‎8.若圆心在x轴上，半径为的圆C位于y轴左侧，且与直线x＋2y＝0相切，则圆C的方程是 (　 　)‎ A. (x－)2＋y2＝5 B. (x＋)2＋y2＝5 C. (x－5)2＋y2＝5 D. (x＋5)2＋y2＝5‎ ‎9.下列四个正方体图形中， 为正方体的两个顶点， 分别为其所在棱的中点，能得出平面的图形的序号是（ ）‎ A. ①③ B. ②④ C. ②③ ‎ D. ①④‎ ‎10.圆台的上、下两个底面圆的半径分别为和，母线与底面的夹角是，则圆台的母线长（ ）‎ A. B. C. D. ‎ ‎11.已知圆 上有且只有两个点到直线 的距离等于1，则半径 的范围是（ ） A. B. C. D.‎ ‎12.已知空间两条不同的直线和两个不同的平面，以下能推出“”的是（ ）‎ A. ， ， B. ， ， ‎ C. ， ， D. ， ， ‎ 二、填空题(共4小题,每小题5分,共20分)‎ ‎13.若直线与圆相交于两点，则 __________．．‎ ‎14.已知三棱锥 ， 面 ， 中两直角边 ， ，该三棱锥的外接球的表面积为 ，则三棱锥的体积为    ．‎ ‎15.已知空间四边形中，对角线，则空间四边形中平行于和的截面四边形的周长的取值范围是____________‎ ‎16.过点，且被圆截得的线段长为的直线方程为__________．‎ 三、解答题(共6小题,共70分)‎ ‎17. （10分）已知直线.‎ ‎（1）求过点且与直线垂直的方程；‎ ‎（2）若直线与两坐标轴所围成的三角形的面积大于4，求实数的取值范围.‎ ‎18. （12分）已知圆的圆心在直线： 上，与直线： 相切，且截直线： 所得弦长为6‎ ‎（Ⅰ）求圆的方程 ‎（Ⅱ）过点是否存在直线，使以被圆截得弦为直径的圆经过原点?若存在，写出直线的方程；若不存在，说明理由.‎ ‎19. （12分）如图，已知正方体 的棱长为3，M，N分别是棱 、 上的点，且 . （1）证明： 四点共面； （2）求几何体 的体积. ‎ ‎20. （12分）如图,点是以为直径的圆周上的一点，,，平面，点为中点.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求直线与平面所成角的大小.‎ ‎21. （12分）如图，在直三棱柱中，是的中点.‎ ‎（1）求证：平面；‎ ‎（2）若，，，求几何体的体积 ‎22. （12分）如图，在直三棱柱中，，，，，分别是，的中点.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）求三棱锥的体积.‎ 参考答案 ‎1.D 2.B 3.C 4.A 5.D 6.D 7.A 8.D 9.D 10.D 11.A 12.C ‎13.‎ ‎14.10‎ ‎15.‎ ‎16.或 ‎17.（1）；（2）.‎ 解：（1)与直线垂直的直线的斜率为， ‎ 因为点在该直线上，所以所求直线方程为，‎ 故所求的直线方程为. ‎ ‎（2）直线与两坐标轴的交点分别为，‎ 则所围成的三角形的面积为， ‎ 由题意可知，化简得， ‎ 解得或，所以实数的取值范围是.‎ ‎18.（1）（2）不存在直线.‎ 解：（Ⅰ）设圆心 ‎∵圆与直线相切 ‎∴‎ ‎∵ 圆截直线： 所得弦长为6‎ ‎∴圆到直线的距离为 ‎∴‎ ‎∴‎ ‎∴圆心， ‎ ‎∴圆的方程 ‎（Ⅱ）①当直线的斜率不存在时， 不符合题意 ‎②设： ‎ 设 ‎∵被圆截得弦为直径的圆经过原点 ‎∴，即 ‎∴‎ 联立直线与圆的方程 化简可得，即 ‎∴， ‎ ‎∵， ， ‎ ‎∴，即 ‎∴‎ ‎∵‎ ‎∴无解 ‎∴不存在直线.‎ ‎19. （1）证明：∵ ， ，又 ， ， ∴ ，且 ， 连接 ，则四边形 是平行四边形， ‎ ‎ 所以 在 中， ， ， 所以 ，所以 所以 ，所以 四点共面. （2）解：因为平面 平面 ， 又 四点共面，所以平面 平面 延长 与 相交于点 ，因为 所以 ，即 ，解得 ，同理可得 ，所以点 与点 重合 所以 三线相交于一点， 所以几何体 是一个三棱台 所以 . ‎ ‎20. （Ⅰ）证明 平面平面平面.‎ ‎（Ⅱ）平面取的中点，连，‎ 则平面，‎ 连，就是直线与平面所成角，‎ ‎，，‎ 所以，‎ 与平面所成角为.‎ ‎21.解：（1）证明：连接，与交于点O，连接DO 由直三棱柱性质可知，侧棱垂直于底面，侧面为矩形，‎ 所以O为中点，‎ 则 又因为平面，平面，‎ 所以：平面；‎ ‎（2）.‎ ‎22.（1）证明见解析；（2）证明见解析；（3）．‎ 解析：（Ⅰ）证明：在三棱柱中，‎ 底面，所以.‎ 又因为，，‎ 所以平面， ‎ 又平面，‎ 所以平面平面 ‎（Ⅱ）证明：取的中点，连接，.‎ 因为，，分别是，，的中点，‎ 所以，且，.‎ 因为，且，所以，且，‎ 所以四边形为平行四边形，所以. ‎ 又因为平面，平面，所以平面. ‎ ‎（Ⅲ）因为，，，所以.‎ 所以三棱锥的体积 ‎. ‎