- 186.35 KB
- 2024-01-05 发布
专题16 用导数研究函数的性质
1.函数的单调性与导数
(1)函数y=f(x)在某个区间内有导数,如果在这个区间内f′(x)>0,那么函数f(x)为这个区间内的增函数;如果在这个区间内f′(x)<0,那么函数f(x)为这个区间内的减函数.
(2)函数f(x)在(a,b)上是增函数,则f′(x)≥0;函数f(x)在(a,b)上是减函数,则f′(x)≤0.
2.函数的极值与导数
(1)若x0满足f′(x0)=0,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点,f(x0)是极值,并且如果f′(x)在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果f′(x)在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值.
(2)f(x)在某个区间内有导数,“f′(x0)=0”是“x0是f(x)的极值点”的必要不充分条件.
3.函数的最值与导数
求解闭区间[a,b]上函数最值的方法:
(1)求极值;
(2)求f(a)、f(b);
(3)比较f(a)、f(b)、极值的大小,确定最大值、最小值.
例1 已知函数f(x)=x3-3x2+3x+1,求函数的单调区间.
变式1 已知函数f(x)=x3+3ax2+3x+1在[2,+∞)上是增函数,求a的取值范围.
例2 已知函数f(x)=x-1+(a∈R,e为自然对数的底数),求函数f(x)的极值.
变式2 设f(x)=-x3+x2+2ax.当00,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
A.2 B.3 C.6 D.9
5.若函数f(x)=x2+ax+在(,+∞)上是增函数,则a的取值范围是________.
6.若f(x)=-x2+bln x在[1,+∞)上是减函数,则b的取值范围是________.
7.设方程x3-3x=k有3个不等的实根,则常数k的取值范围是________.
B级
8.函数y=在定义域内( )
A.有最大值2,无最小值
B.无最大值,有最小值-2
C.有最大值2,最小值-2
D.无最值
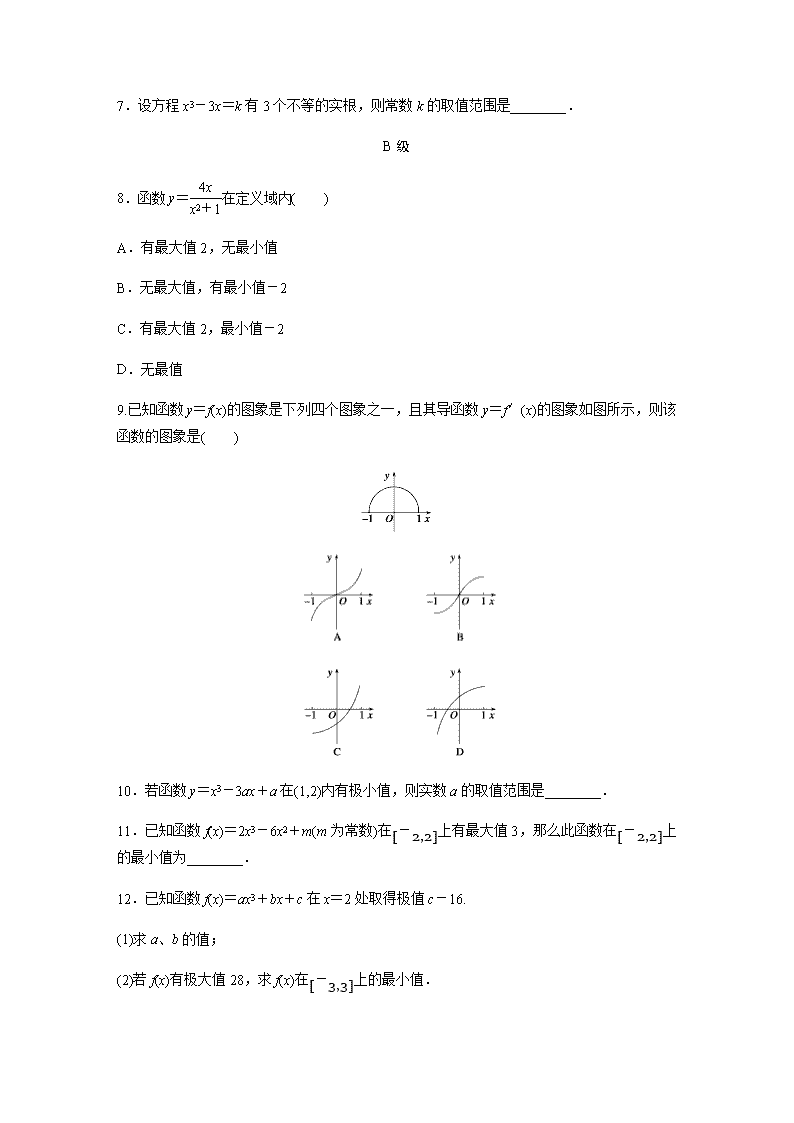
9.已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是( )
10.若函数y=x3-3ax+a在(1,2)内有极小值,则实数a的取值范围是________.
11.已知函数f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为________.
12.已知函数f(x)=ax3+bx+c在x=2处取得极值c-16.
(1)求a、b的值;
(2)若f(x)有极大值28,求f(x)在[-3,3]上的最小值.
13.已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(-∞,-1]上的最大值.
详解答案
典型例题
例1 解 f′(x)=3x2-6x+3.
令f′(x)=0,得x1=-1,x2=+1.
当x∈(-∞,-1)时,f′(x)>0,
f(x)在(-∞,-1)上是增函数;
当x∈(-1,+1)时,f′(x)<0,
f(x)在(-1,+1)上是减函数;
当x∈(-1,+∞)时,f′(x)>0,
f(x)在(+1,+∞)上是增函数.
变式1 解 f′(x)=3(x2+2ax+1),
由题意知,f′(x)=3(x2+2ax+1)≥0在[2,+∞)上恒成立,
即a≥-在[2,+∞)上恒成立,
令g(x)=-,
则g′(x)=-(1-),
显然,x∈[2,+∞)时,g′(x)<0,
即g(x)在[2,+∞)上是减函数,
所以g(x)≤g(2)=-,
所以a的取值范围是[-,+∞).
例2 解 f′(x)=1-,
①当a≤0时,f′(x)>0,f(x)为(-∞,+∞)上的增函数,所以函数f(x)无极值.
②当a>0时,令f′(x)=0,得ex=a,x=ln a.
x∈(-∞,ln a),f′(x)<0;x∈(ln a,+∞),f′(x)>0,
所以f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增,故f(x)在x=ln a处取得极小值且极小值为f(ln a)=ln a,无极大值.
综上,当a≤0时,函数f(x)无极值.
当a>0时,f(x)在x=ln a处取得极小值ln a,无极大值.
变式2 解 由f′(x)=-x2+x+2a=-(x-)2++2a
令f′(x)=0,得两根
x1=,x2=.
所以f(x)在(-∞,x1),(x2,+∞)上单调递减,在(x1,x2)上单调递增.
当00时,f′(x)<0恒成立,
所以函数f(x)的单调递减区间是(0,+∞).
②若b>0,当0时,f′(x)>0.
所以函数f(x)的单调递减区间是,单调递增区间是.
当a>0时,由f′(x)=0得2ax2+bx-1=0.
解得x1=,x2=,
此时x1<0,x2>0.
当0x2时,f′(x)>0.
所以函数f(x)的单调递减区间是,
单调递增区间是.
综上所述:当a=0,b≤0时,函数f(x)的单调递减区间是(0,+∞).
当a=0,b>0时,函数f(x)的单调递减区间是,单调递增区间是.
当a>0时,函数f(x)的单调递减区间是,
单调递增区间是.
变式3 解 由题意知f(x)的定义域为(0,+∞),
f′(x)=+2ax=.
当a≥0时,f′(x)>0,故f(x)在(0,+∞)上单调递增;当a≤-1时,f′(x)<0,故f(x)在(0,+∞)上单调递减;当-10;
当x∈时,f′(x)<0.
故f(x)在上单调递增,
在上单调递减.
综上,当a≥0时,f(x)在(0,+∞)上单调递增;当a≤-1时,f(x)在(0,+∞)上单调递减;当-10,b>0,∴a+b≥2,
∴2≤6,
∴ab≤9,当且仅当a=b=3时等号成立,
∴ab的最大值为9.]
5.[3,+∞)
解析 由题意知f′(x)≥0对任意的x∈恒成立,
又f′(x)=2x+a-,
所以2x+a-≥0对任意的x∈恒成立,
分离参数得a≥-2x,
若满足题意,需a≥max.
令h(x)=-2x,x∈.
因为h′(x)=--2,
所以当x∈时,h′(x)<0,
即h(x)在上单调递减,
所以h(x)<h=3,故a≥3.
6.(-∞,1]
解析 转化为f′(x)=-x+≤0在[1,+∞)上恒成立,
即b≤x2在[1,+∞)上恒成立,
令g(x)=x2,则g(x)min=1,
故b的取值范围是(-∞,1].
7.(-2,2)
解析 设f(x)=x3-3x-k,则f′(x)=3x2-3.
令f′(x)=0得x=±1,且f(1)=-2-k,f(-1)=2-k,又f(x)的图象与x轴有3个交点,故
∴-20时,y′=3x2-3a=0⇒x=±,不难分析,
当1<<2,即1f(2)>f(-2),
∴m=3,最小值为f(-2)=-37.
12.解 (1)因为f(x)=ax3+bx+c,
故f′(x)=3ax2+b,由于f(x)在点x=2处取得极值,故有,
即,
化简得,解得.
(2)由(1)知f(x)=x3-12x+c,f′(x)=3x2-12.
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,
故f(x)在(-∞,-2)上为增函数,
当x∈(-2,2)时,f′(x)<0,
故f(x)在(-2,2)上为减函数;
当x∈(2,+∞)时,f′(x)>0,
故f(x)在(2,+∞)上为增函数.
由此可知f(x)在x1=-2处取得极大值f(-2)=16+c,
f(x)在x2=2处取得极小值f(2)=c-16,由题设条件知16+c=28,得c=12,
此时f(-3)=9+c=21,f(3)=-9+c=3,
f(2)=c-16=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4.
13.解 (1)f′(x)=2ax,g′(x)=3x2+b,
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,
所以f(1)=g(1),且f′(1)=g′(1).
即a+1=1+b,且2a=3+b.
解得a=3,b=3.
(2)记h(x)=f(x)+g(x).当b=a2时,h(x)=x3+ax2+a2x+1,
h′(x)=3x2+2ax+a2.
令h′(x)=0,得x1=-,x2=-.
a>0时,h(x)与h′(x)的变化情况如下表:
所以函数h(x)的单调递增区间为和;
单调递减区间为.
当-≥-1,即06时,函数h(x)在区间上单调递增,在区间上单调递减,在区间上单调递增,
又因为h-h(-1)=1-a+a2=(a-2)2>0,所以h(x)在区间(-∞,-1]上的最大值为h=1.
综上,f(x)+g(x)在(-∞,-1]上的最大值为h(x)max=