- 486.50 KB
- 2023-12-03 发布
绝密★启用前
眉山一中办学共同体2020届第三期半期考试题
数学(理工类)
命题人:杨晓彬 审题人:陈杰
第I卷(选择题)
一、选择题(共60分,每小题5分,每个小题有且仅有一个正确的答案)
1.下列结论正确的个数为( )
A.梯形可以确定一个平面;
B.若两条直线和第三条直线所成的角相等,则这两条直线平行;
C.若l上有无数个点不在平面α内,则l∥α
D.如果两个平面有三个公共点,则这两个平面重合.
2.平面α的法向量为=(1,2,-2),平面β的法向量=(-2,h,k),若α∥β,则h+k的值为( )
A.-2 B.-8 C.0 D.-6
3. 如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,
则下列判断错误的是( )
A.MN与CC1垂直B.MN与AC垂直
C.MN与BD平行D.MN与A1B1平行
4.若直线的方向向量与平面的法向量的夹角等于120°,则直线与平面所成的角等于( )
A.120° B.30° C. 60° D.60°或30°
5. 已知二面角α-l-β的大小是,m,n是异面直线,且m⊥α,n⊥β,则m,n所成的角为( )
A. B. C.D.
6.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.
C. (1,-1,1) D.
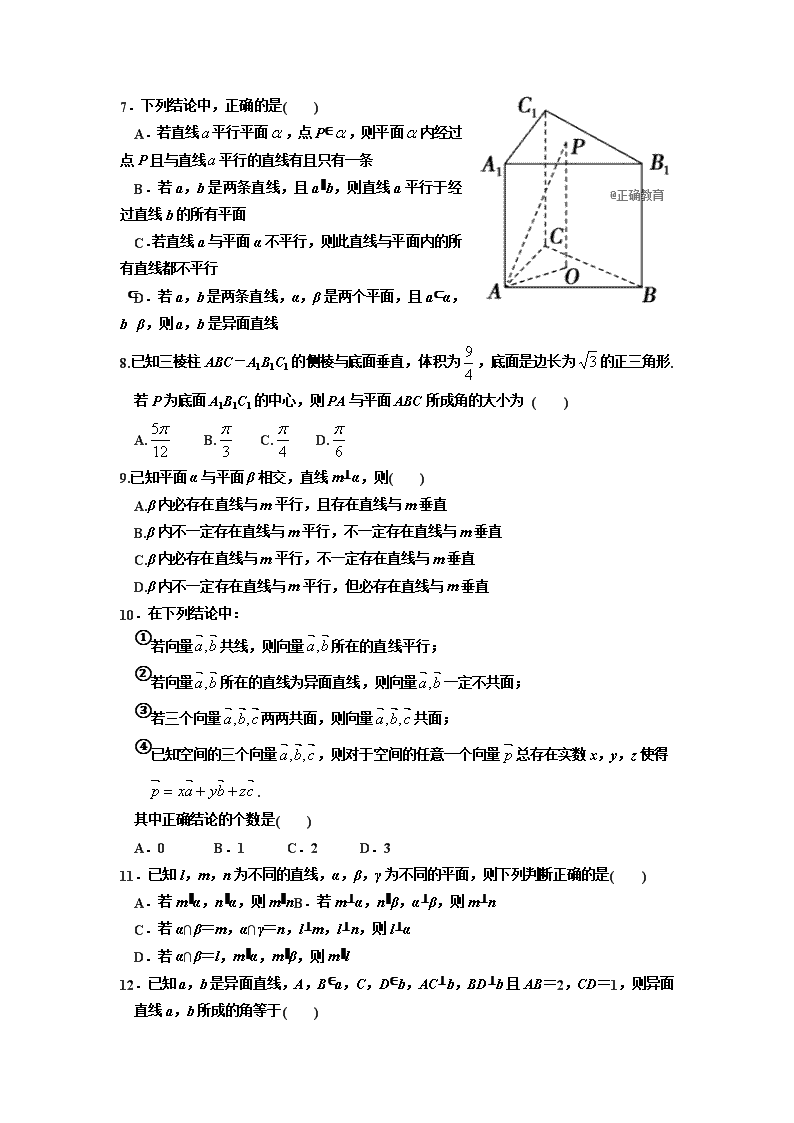
7.下列结论中,正确的是( )
A.若直线平行平面,点P∈,则平面内经过点P且与直线平行的直线有且只有一条
B.若a,b是两条直线,且a∥b,则直线a平行于经过直线b的所有平面
C.若直线a与平面α不平行,则此直线与平面内的所有直线都不平行
D.若a,b是两条直线,α,β是两个平面,且a⊂α,b⊂β,则a,b是异面直线
8.已知三棱柱ABC-A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为 ( )
A. B. C. D.
9.已知平面α与平面β相交,直线m⊥α,则( )
A.β内必存在直线与m平行,且存在直线与m垂直
B.β内不一定存在直线与m平行,不一定存在直线与m垂直
C.β内必存在直线与m平行,不一定存在直线与m垂直
D.β内不一定存在直线与m平行,但必存在直线与m垂直
10.在下列结论中:
①若向量共线,则向量所在的直线平行;
②若向量所在的直线为异面直线,则向量一定不共面;
③若三个向量两两共面,则向量共面;
④已知空间的三个向量,则对于空间的任意一个向量总存在实数x,y,z使得
.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
11.已知l,m,n为不同的直线,α,β,γ为不同的平面,则下列判断正确的是( )
A.若m∥α,n∥α,则m∥nB.若m⊥α,n∥β,α⊥β,则m⊥n
C.若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α
D.若α∩β=l,m∥α,m∥β,则m∥l
12.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b且AB=2,CD=1,则异面直线a,b所成的角等于( )
A.30° B.45° C.60° D.90°
第II卷(非选择题)
二、填空题(共20分,每小题5分)
13.已知向量,,若,则________.
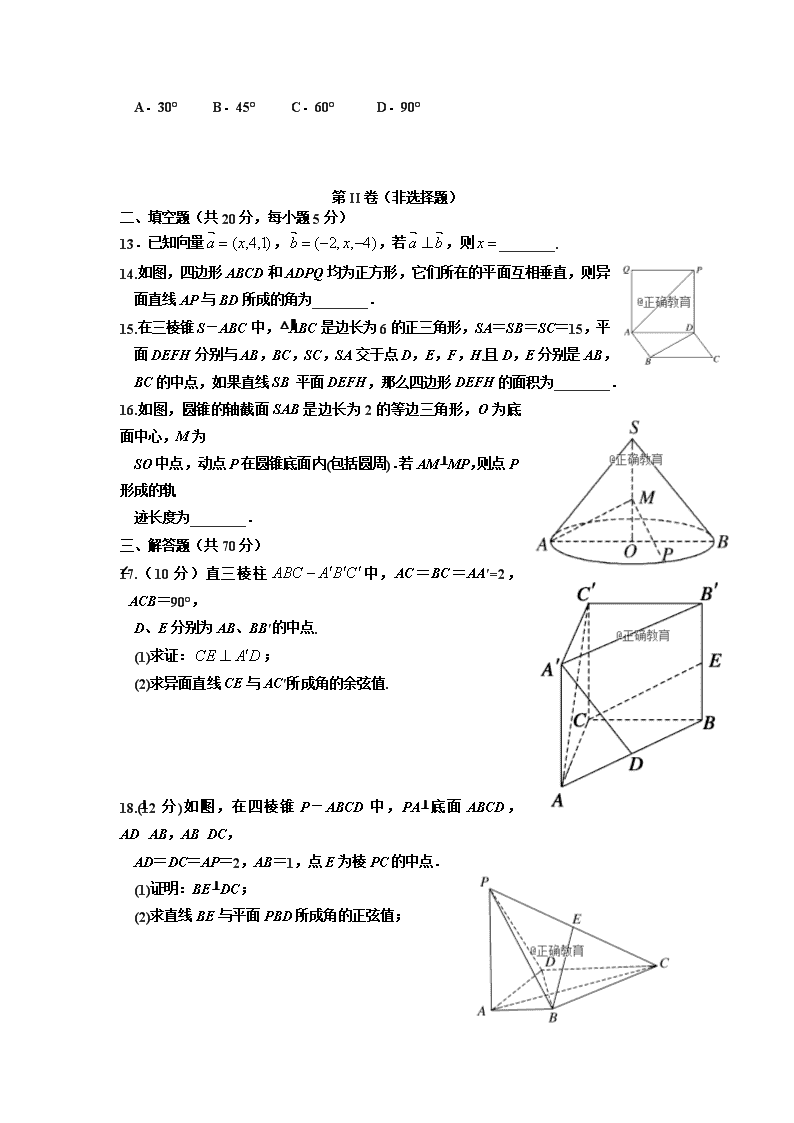
14.如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,则异面直线AP与BD所成的角为________.
15.在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于点D,E,F,H.且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为________.
16.如图,圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为
SO中点,动点P在圆锥底面内(包括圆周).若AM⊥MP,则点P形成的轨
迹长度为________.
三、解答题(共70分)
17.(10分)直三棱柱中,AC=BC=AA′=2,∠ACB=90°,
D、E分别为AB、BB′的中点.
(1)求证:;
(2)求异面直线CE与AC′所成角的余弦值.
18.(12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,
AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
19.(12分)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,
AA1=AC=CB=.
(1)证明:BC1∥平面A1CD;
(2)求二面角D-A1C-E的正弦值.
20.(12分)如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,PA⊥PD,
底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
(1)求B点到平面PCD的距离;
(2)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为?
若存在,求出的值;若不存在,请说明理由.
21. (12分)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,
∠DAB=∠ABC=90°,E是CD的中点.
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,
求四棱锥P-ABCD的体积.
22.(12分)如图,三棱锥的侧面是等腰直角三角形,,,
,且.
(1)求证:平面平面;
(2)求二面角的余弦值.
眉山一中办学共同体2020届第三期半期考试题
数学(理工类)参考答案
一选择题
1A. 2.C 3.D 4.B 5.C 6.B 7.A 8.B 9.D 10.A 11.D 12.C
二填空题
13.2 14. 15. 16.
三解答题
17题(10分)
解:法一:如图建立空间直角坐标系,其各点坐标如图所示
(1) 证明:
(2)
异面直线CE与AC′所成角的余弦值为。
法二:(1)证明 设=a,=b,=c,根据题意,|a|=|b|=|c|,
且a·b=b·c=c·a=0,∴=b+c,=-c+b-a.
∴·=-c2+b2=0.∴⊥,即CE⊥A′D.
(2)解 ∵=-a+c,||=|a|,||=|a|.
·=(-a+c)·=c2=|a|2,∴cos〈,〉==.
即异面直线CE与AC′所成角的余弦值为.
18题(12分)
解:(1)证明 依题意,以点A为原点建立空间直角坐标系如图,
可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(1,1,1)。
=(0,1,1),=(2,0,0),
故·=0,所以BE⊥DC.
(2) =(-1,2,0),=(1,0,-2).
设n=(x,y,z)为平面PBD的一个法向量,
则即不妨令y=1,[5分]可得n=(2,1,1).
于是有cos〈n,〉===,
所以,直线BE与平面PBD所成角的正弦值为.[7分]
19题(12分)
解:(1)证明 连接AC1交A1C于点F,则F为AC1的中点.
又D是AB的中点,连接DF,则BC1∥DF.
因为DF⊂平面A1CD,BC1⊄平面A1CD,
所以BC1∥平面A1CD.
(2)由AC=CB=AB得,AC⊥BC.
以C为坐标原点,的方向为x轴正方向,的方向为y轴正方向,的方向为z轴正方向,建立如图所示的空间直角坐标系Cxyz.
设CA=2,则D(1,1,0),E(0,2,1),A1(2,0,2),
=(1,1,0),=(0,2,1),=(2,0,2).
设n=(x1,y1,z1)是平面A1CD的法向量,
则即可取n=(1,-1,-1).
同理,设m是平面A1CE的法向量,
则可取m=(2,1,-2).
从而cos〈n,m〉==,故sin〈n,m〉=.
即二面角D-A1C-E的正弦值为.
20题(12分).
解:在△PAD中,PA=PD,O为AD中点,∴PO⊥AD.
又∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO⊂平面PAD,∴PO⊥平面ABCD.
在△PAD中,PA⊥PD,PA=PD=,∴AD=2.
在直角梯形ABCD中,O为AD的中点,AB⊥AD,∴OC⊥AD.
以O为坐标原点,OC为x轴,OD为y轴,OP为z轴建立空间直角坐标系,如图所示,
则P(0,0,1),A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),
(1)∴=(1,-1,-1).
设平面PCD的法向量为u=(x,y,z),
则取z=1,得u=(1,1,1).
则B点到平面PCD的距离d==.
(2)设=λ(0≤λ≤1).∵=(0,1,-1),∴-==(0,λ,-λ),
∴=(0,λ,1-λ),∴Q(0,λ,1-λ).
设平面CAQ的法向量为m=(x,y,z),
则取z=1+λ,得m=(1-λ,λ-1,λ+1).
平面CAD的一个法向量为n=(0,0,1),
∵二面角Q-AC-D的余弦值为,
∴|cos〈m,n〉|==.
整理化简,得3λ2-10λ+3=0.解得λ=或λ=3(舍去),∴存在,且=.
21题(12分)
解:方法一 (1)证明 如图,连接AC.由AB=4,BC=3,∠ABC=90°
得AC=5.[1分]又AD=5,E是CD的中点,所以CD⊥AE. [2分]
因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD. [4分]
而PA,AE是平面PAE内的两条相交直线,所以CD⊥平面PAE. [5分]
(2)过点B作BG∥CD,分别与AE,AD相交于点F,G,连接PF.
由(1)CD⊥平面PAE知,BG⊥平面PAE.
于是∠BPF为直线PB与平面PAE所成的角,且BG⊥AE. [6分]
由PA⊥平面ABCD知,∠PBA为直线PB与平面ABCD所成的角. [7分]
由题意得∠PBA=∠BPF,
因为sin∠PBA=,sin∠BPF=,所以PA=BF.
由∠DAB=∠ABC=90°知,AD∥BC.
又BG∥CD,所以四边形BCDG是平行四边形.
故GD=BC=3.于是AG=2.
在Rt△BAG中,AB=4,AG=2,BG⊥AF,所以
BG==2,BF===.于是PA=BF=. [10分]
又梯形ABCD的面积为S=×(5+3)×4=16,
所以四棱锥P-ABCD的体积为V=×S×PA=×16×=. [12分]
方法二 如图,以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立
空间直角坐标系.设PA=h,
则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h). [2分]
(1)证明 易知=(-4,2,0),=(2,4,0),=(0,0,h).
因为·=-8+8+0=0,·=0, [4分]
所以CD⊥AE,CD⊥AP.
而AP,AE是平面PAE内的两条相交直线,
所以CD⊥平面PAE. [5分]
(2)由题设和(1)知,,分别是平面PAE,平面ABCD的法向量. [6分]
而PB与平面PAE所成的角和PB与平面ABCD所成的角相等,
所以|cos〈,〉|=|cos〈,〉|,
即=
. [8分]
由(1)知,=(-4,2,0),=(0,0,-h),
又=(4,0,-h),
故=.解得h=. [10分]
又梯形ABCD的面积为S=×(5+3)×4=16,
所以四棱锥P-ABCD的体积为V=×S×PA=×16×=. [12分]
22.(本小题满分12分)
解:(1)证明:如图,取BD中点E,连结、, 1分
因为是等腰直角三角形,
所以, 2分
设,则, 3分
在中,由余弦定理得:
, 4分
因为,,
所以,即, 5分
又,,
所以平面,
所以平面平面; 6分
(2)解法一:过点E在平面内作交于点F,由(I)知平面,
分别以为x轴,y轴,z轴建立如图空间直角坐标系, 7分
不妨设,
则:, 8分
则,,, 9分
设平面的法向量,
则,取, 10分
设平面的法向量,
则,取, 11分
所以,
因为二面角的平面角是锐角,
所以二面角的余弦值为. 12分
解法二:过点D作DN⊥AC于点N,
设D在平面ABC上的射影为M,连接MN,
则AC⊥MN,所以∠DNM为所求二面角的平面角, 7分
设AB=1,则AD=1,BD=CD=,AC=2,BC=,
在△ADC中,cos∠DAC=,
所以DN=, 8分
在△ABC中,cos∠BAC=,所以sin∠BAC=, 9分
由,
所以,
即, 11分
在△DMN中,sin∠DNM=,
所以cos∠DNM=,
所以二面角的余弦值为. 12分