- 160.87 KB
- 2021-06-26 发布
考点34空间直角坐标系、空间向量及其运算
解答题
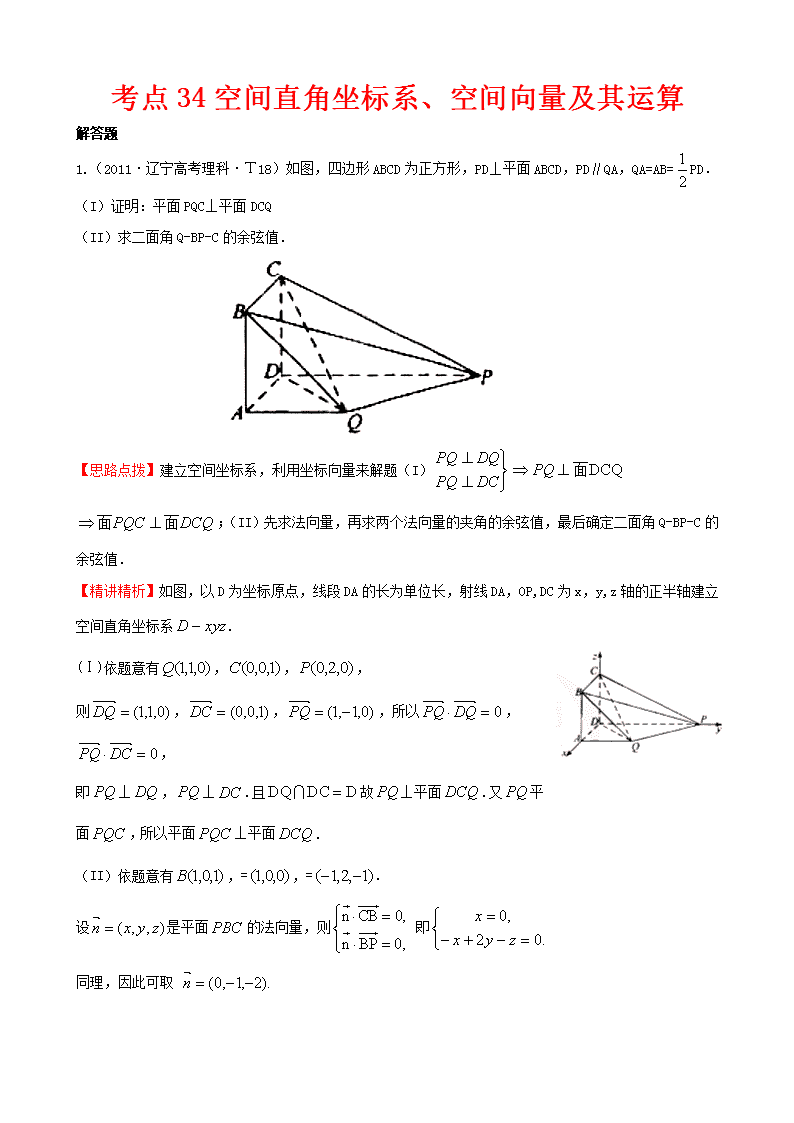
1.(2011·辽宁高考理科·T18)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.
(I)证明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
【思路点拨】建立空间坐标系,利用坐标向量来解题(I)
;(II)先求法向量,再求两个法向量的夹角的余弦值,最后确定二面角Q-BP-C的余弦值.
【精讲精析】如图,以D为坐标原点,线段DA的长为单位长,射线DA,OP,DC为x,y,z轴的正半轴建立空间直角坐标系.
(Ⅰ)依题意有,,,
则,,,所以,,
即 ⊥,⊥.且故⊥平面.又平面,所以平面⊥平面.
(II)依题意有,=,=.
设是平面的法向量,则 即
同理,因此可取
设是平面的法向量,则
可取所以且由图形可知二面角为钝角
故二面角的余弦值为
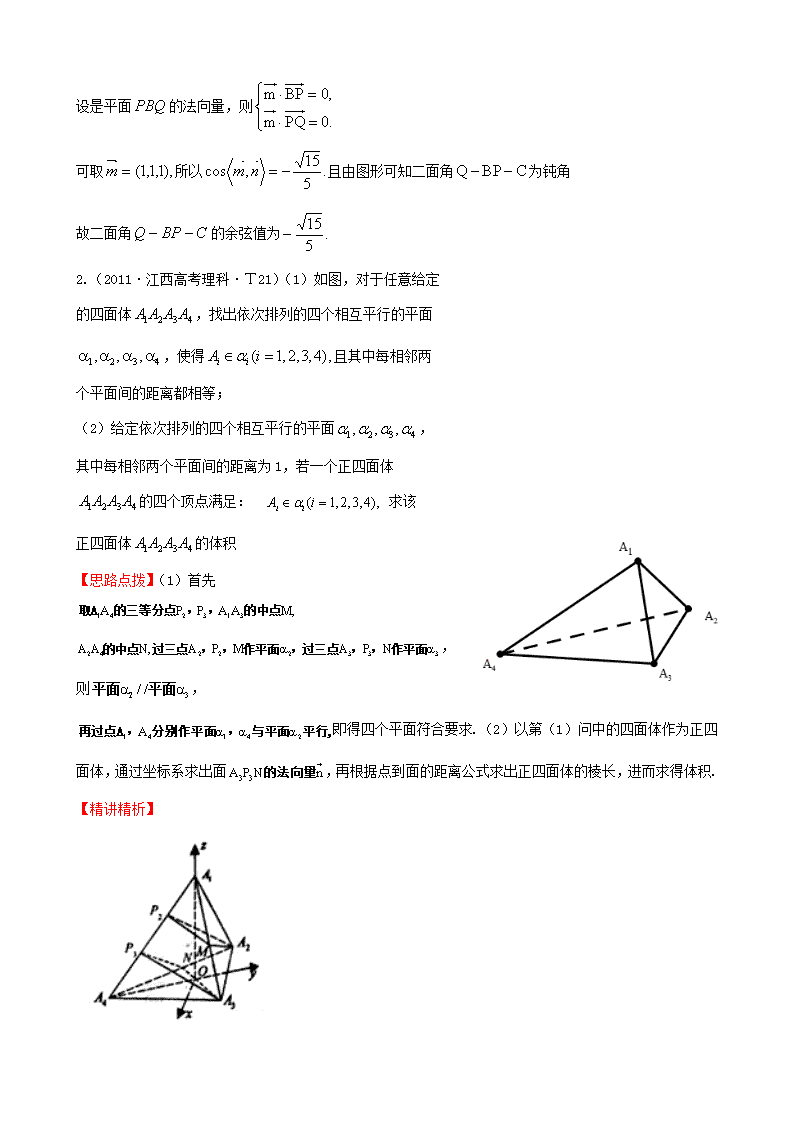
2.(2011·江西高考理科·T21)(1)如图,对于任意给定
的四面体,找出依次排列的四个相互平行的平面
,使得且其中每相邻两
个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面,
其中每相邻两个平面间的距离为1,若一个正四面体
的四个顶点满足: 求该
正四面体的体积
【思路点拨】(1)首先
,则,
即得四个平面符合要求.(2)以第(1)问中的四面体作为正四面体,通过坐标系求出面,再根据点到面的距离公式求出正四面体的棱长,进而求得体积.
【精讲精析】
3.(2011.天津高考理科.T17)如图,在三棱柱中,
是正方形的中心,,平面,
且
(Ⅰ)求异面直线AC与A1B1所成角的余弦值;
(Ⅱ)求二面角的正弦值;
(Ⅲ)设为棱的中点,点在平面内,且平面,求线段的长.
【精讲精析】 方法一:如图所示,建立空间直角坐标系,点B为坐标原点.
依题意得
(I)易得,
于是
所以异面直线AC与A1B1所成角的余弦值为
(II)易知,设平面AA1C1的法向量,
则即不妨令可得,
同样地,设平面A1B1C1的法向量,
则即不妨令,
可得于是从而
所以二面角A—A1C1—B1的正弦值为
(III)由N为棱B1C1的中点,得
设M(a,b,0),则),由
平面A1B1C1,得
即
解得故
因此,所以线段BM的长为
方法二:
(I)由于AC//A1C1,故是异面直线AC与A1B1所成的角.
因为平面AA1B1B,又H为正方形AA1B1B的中心,
可得
因此
所以异面直线AC与A1B1所成角的余弦值为
(II)连接AC1,易知AC1=B1C1,
又由于AA1=B1A1,A1C1=A1C1,
所以≌,过点A作于点R,
连接B1R,于是,故为二面角A—A1C1—B1的平面角.
在中,
连接AB1,在中,
,
从而
所以二面角A—A1C1—B1的正弦值为
(III)因为平面A1B1C1,所以,取HB1中点D,连接ND,由于N是棱B1C1中点,所以ND//C1H且.又平面AA1B1B,
所以平面AA1B1B,故又
所以平面MND,连接MD并延长交A1B1于点E,则
由得,延长EM交AB于点F,
可得连接NE.在中,
所以可得连接BM,在中,
相关文档
- 2021版高考数学一轮复习核心素养测2021-06-26 02:09:478页
- 2017-2018学年陕西省西安市长安区2021-06-26 02:09:219页
- 吉林省辽源市田家炳高级中学(第六十2021-06-26 02:09:0810页
- 2017-2018学年重庆市第一中学高二2021-06-26 02:08:5511页
- 2006高考语文试卷:天津卷(含答案)2021-06-26 02:08:4215页
- 四川省南充市2019-2020学年高二下2021-06-26 02:08:279页
- 2019-2020学年云南省昆明市官渡区2021-06-26 02:08:2513页
- (浙江专版)2020高考历史一轮复习 第2021-06-26 02:08:1214页
- 河北省武邑中学2018-2019学年高二12021-06-26 02:07:5716页
- 2021高考英语一轮复习MoeandPopArt2021-06-26 02:07:449页