2013四川卷（文）数学试题 8页

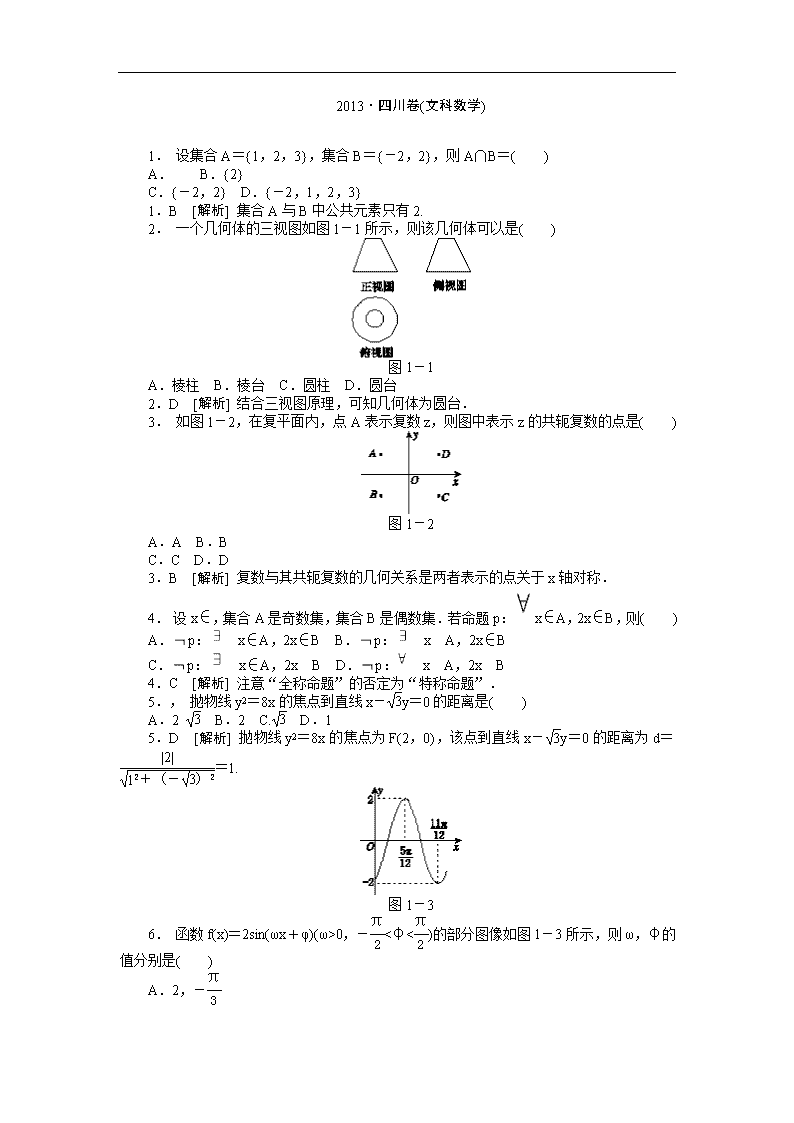
‎2013·四川卷(文科数学)‎ ‎　　　　　　　　　　　　　　　　　　　‎ ‎1． 设集合A＝{1，2，3}，集合B＝{－2，2}，则A∩B＝(　　)‎ A． B．{2}‎ C．{－2，2} D．{－2，1，2，3}‎ ‎1．B　[解析] 集合A与B中公共元素只有2.‎ ‎2． 一个几何体的三视图如图1－1所示，则该几何体可以是(　　)‎ 图1－1‎ A．棱柱 B．棱台 C．圆柱 D．圆台 ‎2．D　[解析] 结合三视图原理，可知几何体为圆台．‎ ‎3． 如图1－2，在复平面内，点A表示复数z，则图中表示z的共轭复数的点是(　　)‎ 图1－2‎ A．A B．B C．C D．D ‎3．B　[解析] 复数与其共轭复数的几何关系是两者表示的点关于x轴对称．‎ ‎4． 设x∈，集合A是奇数集，集合B是偶数集．若命题p：x∈A，2x∈B，则(　　)‎ A．p：x∈A，2x∈B B．p：xA，2x∈B C．p：x∈A，2xB D．p：xA，2xB ‎4．C　[解析] 注意“全称命题”的否定为“特称命题”．‎ ‎5．， 抛物线y2＝8x的焦点到直线x－y＝0的距离是(　　)‎ A．2 B．2 C. 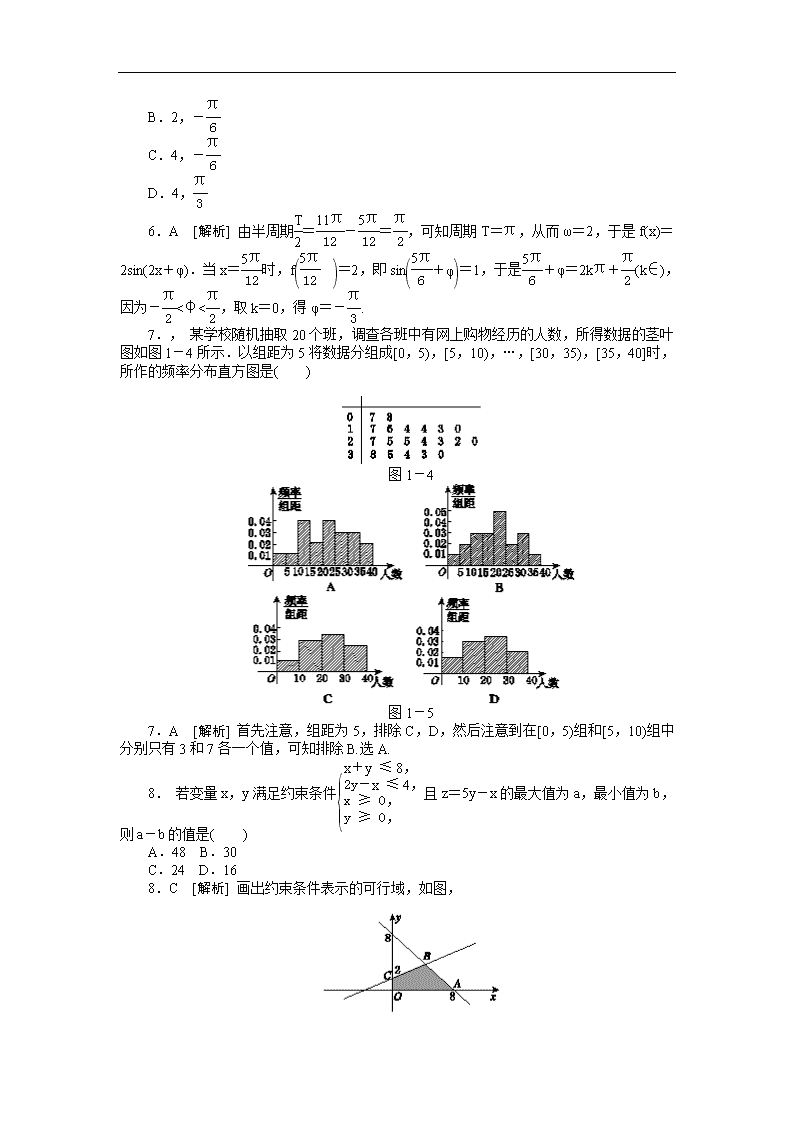D．1‎ ‎5．D　[解析] 抛物线y2＝8x的焦点为F(2，0)，该点到直线x－y＝0的距离为d＝＝1.‎ 图1－3‎ ‎6． 函数f(x)＝2sin(ωx＋φ)(ω>0，－<φ<)的部分图像如图1－3所示，则ω，φ的值分别是(　　)‎ A．2，－ ‎ B．2，－ C．4，－ ‎ D．4， ‎6．A　[解析] 由半周期＝－＝，可知周期T＝π，从而ω＝2，于是f(x)＝2sin(2x＋φ)．当x＝时，f＝2，即sin＝1，于是＋φ＝2kπ＋(k∈)，因为－<φ<，取k＝0，得φ＝－.‎ ‎7．， 某学校随机抽取20个班，调查各班中有网上购物经历的人数，所得数据的茎叶图如图1－4所示．以组距为5将数据分组成[0，5)，[5，10)，…，[30，35)，[35，40]时，所作的频率分布直方图是(　　)‎ 图1－4‎ 图1－5‎ ‎7．A　[解析] 首先注意，组距为5，排除C，D，然后注意到在[0，5)组和[5，10)组中分别只有3和7各一个值，可知排除B.选A.‎ ‎8． 若变量x，y满足约束条件且z＝5y－x的最大值为a，最小值为b，则a－b的值是(　　)‎ A．48 B．30‎ C．24 D．16‎ ‎8．C　[解析] 画出约束条件表示的可行域，如图，‎ 由于目标函数z＝5y－x的斜率为，可知在点A(8，0)处，z取得最小值b＝－8，在点B(4，4)处，z取得最大值a＝16.故a－b＝24.‎ ‎9． 从椭圆＋＝1(a>b>0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP(O是坐标原点)，则该椭圆的离心率是(　　)‎ A. B. C. D. ‎9．C　[解析] 由已知，P点坐标为，A(a，0)，B(0，b)，于是由kAB＝kOP得－＝，整理得b＝c，从而a＝＝c.于是，离心率e＝＝.‎ ‎10．， 设函数f(x)＝(a∈，e为自然对数的底数)．若存在b∈[0，1]使f(f(b))＝b成立，则a的取值范围是(　　)‎ A．[1，e] B．[1，1＋e]‎ C．[e，1＋e] D．[0，1]‎ ‎10．A　[解析] 易得f(x)在[0，1]上是增函数，对于b∈[0，1]，如果f(b)＝c＞b，则f(f(b))＝f(c)＞f(b)＝c＞b，不可能有f(f(b))＝b；同理，当f(b)＝d＜b时，则f(f(b))＝f(d)＜f(b)＝d＜b，也不可能有f(f(b))＝b；因此必有f(b)＝b，即方程f(x)＝x在[0，1]上有解，即＝x.因为x≥0，两边平方得ex＋x－a＝x2，所以a＝ex－x2＋x.记g(x)＝ex－x2＋x，则g′(x)＝ex－2x＋1.‎ 当x∈时，ex＞0，－2x＋1≥0，故g′(x)＞0.‎ 当x∈时，ex＞＞1，－2x＋1≥－1，故g′(x)＞0，综上，g′(x)在x∈[0，1]上恒大于0，所以g(x)在[0，1]上为增函数，值域为[g(0)，g(1)]，即[1，e]，从而a的取值范围是[1，e]．‎ ‎11． lg ＋lg 的值是________．‎ ‎11．1　[解析] lg ＋lg ＝lg (·)＝lg ＝lg 10＝1.‎ ‎12． 如图1－6，在平行四边形ABCD中，对角线AC与BD交于点O，＋＝λ，则λ＝________.‎ 图1－6‎ ‎12．2　[解析] 根据向量运算法则，＋＝＝2，故λ＝2.‎ ‎13． 已知函数f(x)＝4x＋(x>0，a>0)在x＝3时取得最小值，则a＝________.‎ ‎3．36　[解析] 由基本不等式性质，f(x)＝4x＋(x>0，a>0)在4x＝，即x2＝时取得最小值，由于x＞0，a＞0，再根据已知可得＝32，故a＝36.‎ ‎14．，， 设sin 2α＝－sin α，α∈(，π)，则tan 2α的值是________．‎ ‎14.　[解析] 方法一：由已知sin 2α＝－sin α，即2sin αcos α＝－sin α，又α∈，故sin α≠0，于是cos α＝－，进而sin α＝，于是tan α＝－，所以tan 2α＝＝＝.‎ 方法二：同上得cos α＝－，又α∈，可得α＝，所以tan 2α＝tan ＝.‎ ‎15．，， 在平面直角坐标系内，到点A(1，2)，B(1，5)，C(3，6)，D(7，－1)的距离之和最小的点的坐标是________．‎ ‎15．(2，4)　[解析] 在以A，B，C，D为顶点构成的四边形中，由平面几何知识：三角形两边之和大于第三边，可知当动点落在四边形两条对角线AC，BD交点上时，到四个顶点的距离之和最小．AC所在直线方程为y＝2x，BD所在直线方程为y＝－x＋6，交点坐标为(2，4)，即为所求．‎ ‎16．， 在等比数列{an}中，a2－a1＝2，且2a2为3a1和a3的等差中项，求数列{an}的首项、公比及前n项和．‎ ‎16．解：设该数列的公比为q，由已知，可得 a1q－a1＝2，4a1q＝3a1＋a1q2，‎ 所以，a1(q－1)＝2，q2－4q＋3＝0，解得q＝3或q＝1.‎ 由于a1(q－1)＝2，因此q＝1不合题意，应舍去．‎ 故公比q＝3，首项a1＝1.‎ 所以，数列的前n项和Sn＝.‎ ‎17．，， 在△ABC中，角A，B，C的对边分别为a，b，c，且cos(A－B)cos B－sin(A－B)sin(A＋C)＝－.‎ ‎(1)求sin A的值；‎ ‎(2)若a＝4 ，b＝5，求向量在方向上的投影．‎ ‎17．解：(1)由cos(A－B)cos B－sin(A－B)sin(A＋C)＝－，‎ 得cos(A－B)cos B－sin(A－B)sin B＝－.‎ 则cos(A－B＋B)＝－，即cos A＝－.‎ 又0b，则A>B，故B＝.‎ 根据余弦定理，有 ‎(4 )2＝52＋c2－2×5c×，‎ 解得c＝1或c＝－7(负值舍去)．‎ 故向量在方向上的投影为||cos B＝.‎ 图1－7‎ ‎18．， 某算法的程序框图如图1－7所示，其中输入的变量x在1，2，3，…，24这24个整数中等可能随机产生．‎ ‎(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i＝1，2，3)；‎ ‎(2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i(i＝1，2，3)的频数．以下是甲、乙所作频数统计表的部分数据．‎ 甲的频数统计表(部分)‎ 运行 次数n 输出y的值 为1的频数 输出y的值 为2的频数 输出y的值 为3的频数 ‎30‎ ‎14‎ ‎6‎ ‎10‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎2 100‎ ‎1 027‎ ‎376‎ ‎697‎ 乙的频数统计表(部分)‎ 运行 次数n 输出y的值 为1的频数 输出y的值 为2的频数 输出y的值 为3的频数 ‎30‎ ‎12‎ ‎11‎ ‎7‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎2 100‎ ‎1 051‎ ‎696‎ ‎353‎ 当n＝2 100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i(i＝1，2，3)的频率(用分数表示)，并判断两位同学中哪一位所编写程序符合算法要求的可能性较大．‎ ‎18．解：(1)变量x是在1，2，3，…，24这24个整数中随机产生的一个数，共有24种可能．‎ 当x从1，3，5，7，9，11，13，15，17，19，21，23这12个数中产生时，输出y的值为1，故P1＝；‎ 当x从2，4，8，10，14，16，20，22这8个数中产生时，输出y的值为2，故P2＝；‎ 当x从6，12，18，24这4个数中产生时，输出y的值为3，故P3＝.‎ 所以，输出y的值为1的概率为，输出y的值为2的概率为，输出y的值为3的概率为.‎ ‎(2)当n＝2 100时，甲、乙所编程序各自输出y的值为i(i＝1，2，3)的频率如下：‎ 输出y的值 为1的频率 输出y的值 为2的频率 输出y的值 为3的频率 甲 乙 比较频率趋势与(1)中所求的概率，可得乙同学所编程序符合算法要求的可能性较大．‎ ‎19．，，， ‎ 图1－8‎ 如图1－8，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB＝AC＝2AA1＝2，∠BAC＝120°，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．‎ ‎(1)在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；‎ ‎(2)设(1)中的直线l交AC于点Q，求三棱锥A1－QC1D的体积．(锥体体积公式：V＝Sh，其中S为底面面积，h为高)‎ ‎19．解：(1)如图，在平面ABC内，过点P作直线l∥BC，因为l在平面A1BC外，BC在平面A1BC内，由直线与平面平行的判定定理可知，l∥平面A1BC.‎ 由已知，AB＝AC，D是BC的中点，‎ 所以，BC⊥AD，则直线l⊥AD.‎ 因此AA1⊥平面ABC，所以AA1⊥直线l.‎ 又因为AD，AA1在平面ADD1A1内，且AD与AA1相交，‎ 所以直线l⊥平面ADD1A1.‎ ‎(2)过D作DE⊥AC于E.‎ 因为AA1⊥平面ABC，所以DE⊥AA1.‎ 又因为AC，AA1在平面AA1C1C内，且AC与AA1相交，‎ 所以DE⊥平面AA1C1C.‎ 由AB＝AC＝2，∠BAC＝120°，有AD＝1，∠DAC＝60°，‎ 所以在△ACD中，DE＝AD＝.‎ 又S△A1QC1＝A1C1·AA1＝1，所以 VA1－QC1D＝VD－A1QC1＝DE·S△A1QC1＝××1＝.‎ 因此三棱锥A1－QC1D的体积是.‎ ‎20．，， 已知圆C的方程为x2＋(y－4)2＝4，点O是坐标原点．直线l：y＝kx与圆C交于M，N两点．‎ ‎(1)求k的取值范围；‎ ‎(2)设Q(m，n)是线段MN上的点，且＝＋.请将n表示为m的函数．‎ ‎20．解：(1)将y＝kx代入x2＋(y－4)2＝4，得 ‎(1＋k2)x2－8kx＋12＝0.(*)‎ 由Δ＝(－8k)2－4(1＋k2)×12>0，得k2>3.‎ 所以，k的取值范围是(－∞，－)∪(＋∞)．‎ ‎(2)因为M，N在直线l上，可设点M，N的坐标分别为(x1，kx1)，(x2，kx2)，则 ‎|OM|2＝(1＋k2)x，|ON|2＝(1＋k2)x.‎ 又|OQ|2＝m2＋n2＝(1＋k2)m2，‎ 由＝＋，得 ＝＋，‎ 即＝＋＝.‎ 由(*)式可知，x1＋x2＝，x1x2＝，‎ 所以m2＝.‎ 因为点Q在直线y＝kx上，所以k＝，代入m2＝中并化简，得5n2－3m2＝36.‎ 由m2＝及k2>3，可知00，‎ 所以n＝＝.‎ 于是，n与m的函数关系为n＝(m∈(－，0)∪(0，))．‎ ‎21．，， 已知函数f(x)＝其中a是实数．设A(x1，f(x1))，B(x2，f(x2))为该函数图像上的两点，且x10，‎ 因此x2－x1＝[－(2x1＋2)＋2x2＋2]≥＝1.‎ ‎(当且仅当－(2x1＋2)＝2x2＋2＝1，即x1＝－且x2＝－时等号成立)‎ 所以，函数f(x)的图像在点A，B处的切线互相垂直时，有x2－x1≥1.‎ ‎(3)当x1x1>0时，f′(x1)≠f′(x2)，故x1<00时，函数f(x)的图像在点(x2，f(x2))处的切线方程为y－ln x2＝(x－x2)，即y＝·x＋ln x2－1.‎ 两切线重合的充要条件是 由①及x1<0h(2)＝－ln 2－1，‎ 所以a>－ln2－1，‎ 而当t∈(0，2)且t趋近于0时，h(t)无限增大，‎ 所以a的取值范围是(－ln 2－1，＋∞)．‎ 故当函数f(x)的图像在点A，B处的切线重合时，a的取值范围是(－ln 2－1，＋∞)．‎