2015年数学理高考课件3-3 三角函数的图象与性质 40页

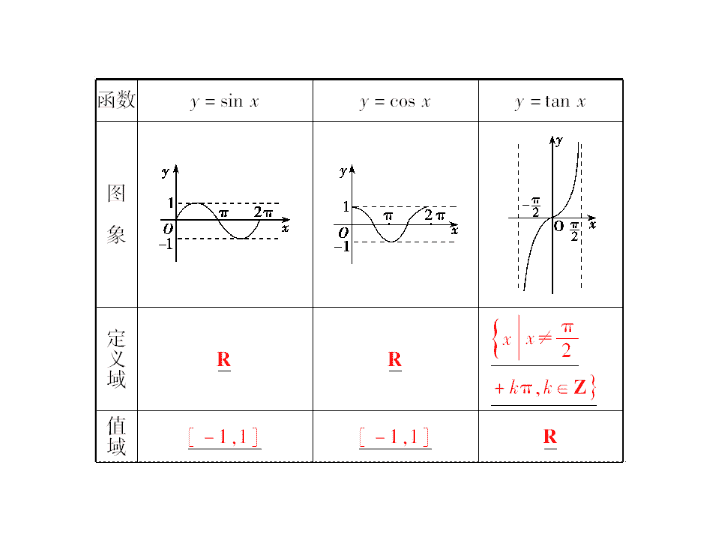
第三节　三角函数的图象与性质 正弦函数、余弦函数、正切函数的图象和性质 答案： D 答案： A 3 ． (2014 年云南模拟 ) 已知 a 是实数，则函数 f ( x ) ＝ a cos ax 的图象可能是 ( 　　 ) 答案： C 三角函数的定义域　值域 反思总结 1 ． 求三角函数的定义域实际上是解简单的三角不等式，常借助三角函数线或三角函数图象来求解． 2 ．求解三角函数的值域 ( 最值 ) 常见到以下几种类型的题目 (1) 形如 y ＝ a sin x ＋ b cos x ＋ c 的三角函数化为 y ＝ A sin( ωx ＋ φ ) ＋ k 的形式，再求最值 ( 值域 ) ； (2) 形如 y ＝ a sin 2 x ＋ b sin x ＋ c 的三角函数，可先设 sin x ＝ t ，化为关于 t 的二次函数求值域 ( 最值 ) ． 变式训练 1 ．求函数 y ＝ (4 － 3sin x )(4 － 3cos x ) 的最小值． 三角函数的单调性 反思总结 1 ． 熟练掌握正、余弦函数 y ＝ sin x 、 y ＝ cos x 单调区间是迅速正确求解正、余弦型函数的单调区间的关键．特别提醒，当单调区间有无穷多个时，别忘了注明 k ∈ Z . 2 ．在求 y ＝ A sin( ωx ＋ φ ) 的单调区间时，要特别注意 A 和 ω 的符号，若 ω <0 ，则通过诱导公式先将 ω 化正再求． 答案： A 三角函数的奇偶性与周期性、对称性 [ 答案 ] 　 (1)D 　 (2)C 　 (3)C 答案： A —— 已知三角函数单调性求参数值或范围 已知单调性求参数值或参数范围是最近几年命题的热点，逆向考查三角函数的单调性，常见命题角度有： (1) 已知三角函数单调性求参数值． (2) 已知三角函数在某区间上单调求参数范围． 已知三角函数单调性求参数值 [ 答案 ] 　 C 由题悟道 解答此类问题要注意结合 y ＝ sin ωx 的递增、递减区间，确立单调区间端点值，建立方程．以待定系数． 利用三角函数在某区间上的单调性求参数范围 [ 答案 ] 　 B 答案： A 本小节结束 请按 ESC 键返回