- 327.00 KB
- 2021-06-23 发布
数学(文)试卷
命题:张世源 审题:邱火明 校稿:曾观育
一、选择题(共12题,每题5分)
1、要比较甲乙两位同学谁的数学成绩更加稳定,选项中最有说服力的数据是( )
A.两位同学近10次成绩的平均数 B.两位同学近10次成绩的方差
C.两位同学近10次成绩的中位数 D.两位同学近10次成绩的众数
2、为这个椭圆上的一点,则点满足( )
A. B.
C. D.
3、空间直角坐标系中,,,则( )
A. 2 B. C. D. 4
4、在某次数学测验后,将参加考试的500名学生的数学成绩制成频率分布直方图(如图),则在该次测验中成绩不低于100分的学生数是( )
A. 210 B. 205 C. 200 D. 195
5、为了解某校老年、中年和青年教师的身体状况,已知老、中、青人数之比为3:7:5,现用分层抽样的方法抽取容量为n的样本,其中老年教师有18人,则样本容量n=( )
A. 45 B. 54 C. 90 D. 126
6、若一个圆锥的轴截面是面积为1的等腰直角三角形,则这个圆锥的体积是( )
A. B. C. D.
7、袋中装有3个黑球,4个白球,从中任取4个球,则在下列事件中,是互斥事件但不是对立事件的是( )
A恰有1个白球和至多有1个黑球; B至少有2个白球和恰有3个黑球;
C至少有1个黑球和全是白球; D至少有1个白球和至少有1个黑球;
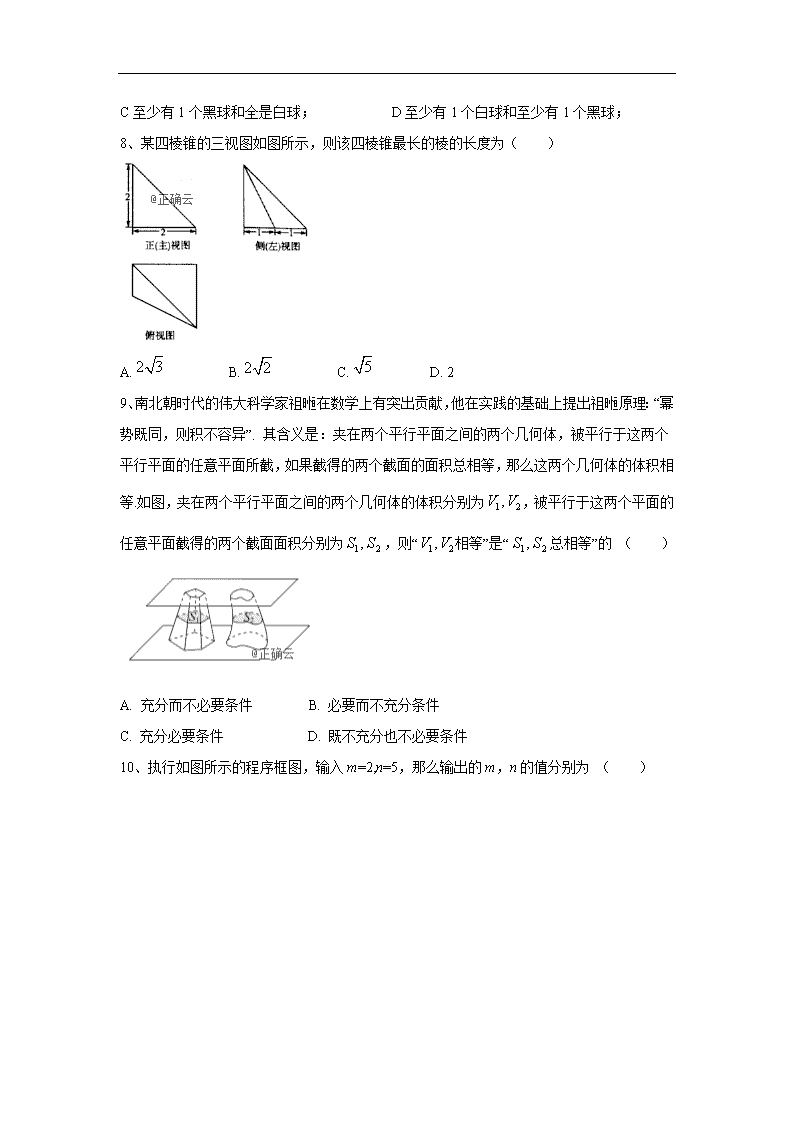
8、某四棱锥的三视图如图所示,则该四棱锥最长的棱的长度为( )
A. B. C. D. 2
9、南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为,被平行于这两个平面的任意平面截得的两个截面面积分别为,则“相等”是“总相等”的 ( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10、执行如图所示的程序框图,输入m=2,n=5,那么输出的m,n的值分别为 ( )
A. 7,-3 B. -3,-3 C. 5, -3 D. 5,2
11、椭圆,分别为椭圆的两焦点,点为椭圆上一点且,则点到轴的距离为( )
A. B. C. D.
16、甲、乙两人约定于6时到7时之间在某地会面,则甲比乙早到会面地点15分钟以上的概率为( )。
A. B. C. D.
二、填空题(共4题,每题5分)
13、7名学生,其中3名男生4名女生。现用抽签法从中抽一人,则抽到的是男生的概率为____。
14、命题的必要而不充分条件,则实数的最大值是____。
15、数列共10项,已知这10项数据的平均值和方差都是2;数列共10项且满足。记数列中10项数据的平均值为,方差为,则
=____。
16、如图,已知三棱柱ABC-A1B1C1的侧面都是正方形,且AA1⊥底面ABC,M是侧棱BB1的中点,则异面直线AC1和CM所成的角为____。
三、解答题(共6题,17题10分,18~22每题12分)
17、焦点在轴上的椭圆,点在椭圆上。
(1)求的值。
(2)依次求出这个椭圆的长轴长、短轴长、焦距、离心率。
18、如图,梯形中,于,于,且,现将,分别沿与翻折,使点与点重合。
(1)证明:;
(2)求四棱锥的体积。
A
F
E
D
B
C
19、某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温。
(1)求线性回归方程;(参考数据:,)
(2)根据回归方程估计当气温为10℃时的用电量。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:,.
20、已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样。
(1)若第五组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的中位数;
(3)在(2)的条件下,从体重不低于73公斤的职工中随机抽取两名职工,求被抽到的两名职工的体重之和等于154公斤的概率。
(1)若命题为真命题,求实数的取值范围;
(2)若命题“”为真命题,命题“”为假命题,求实数的取值范围。
22、已知椭圆的离心率为,长轴长为4,直线与椭圆C交于A、B两点且为直角,O为坐标原点.
(1)求椭圆C的方程;
(2)求的值。
数学(文)答案
一、选择题:
1
2
3
4
5
6
7
8
9
10
11
12
B
A
B
C
C
D
A
A
B
D
D
C
二、填空题:
13、 14、-2 15、24 16、
三、解答题:
17、(1)将点P的坐标带入椭圆,解得m=2
(2).长轴长4、短轴长、焦距、离心率
18、(1).
(2).
19、解:
把代入回归方程得,解得.
回归方程为;
当时,,估计当气温为时的用电量为30度.
20、(1)由题意,第5组抽出的号码为22.因为2+5×(5-1)=22,所以第1组抽出的号码应该为2,抽出的10名职工的号码依次分别为:2,7,12,17,22,27,32,37,42,47.
(2)这10名职工的体重中位数为:(70+73)2=71.5
(3)
从这10名职工中随机抽取两名体重不轻于73公斤的职工,共有10种不同的取法:(73,76),(73,78),(73,79),(73,81),(76,78),(76,79),(76,81),(78,79),(78,81),(79,81),其中体重之和大于等于154公斤的有7种.故所求概率P=.
21、(1)∵命题p:“∀x∈[1,2],x2﹣a≥0”,令f(x)=x2﹣a,
根据题意,只要x∈[1,2]时,f(x)min≥0即可,
也就是1﹣a≥0,解得a≤1,
∴实数a的取值范围是(﹣∞,1];
(2)由(1)可知,当命题p为真命题时,a≤1,
命题q为真命题时,△=4a2﹣4(2﹣a)≥0,解得a≤﹣2或a≥1.
∵命题“p∨q”为真命题,命题“p∧q”为假命题,
∴命题p与命题q必然一真一假,
当命题p为真,命题q为假时,,
当命题p为假,命题q为真时,,
综上:a>1或﹣2<a<1.
22、(1)由题意, ,, 所以.
椭圆方程为
(2)设,,把代人,得.
因为为直角,所以,
得即
由韦达定理:,
代入上式得:,解得