安徽省定远县育才学校2020届高三数学（文）6月模拟试题（Word版附答案） 18页

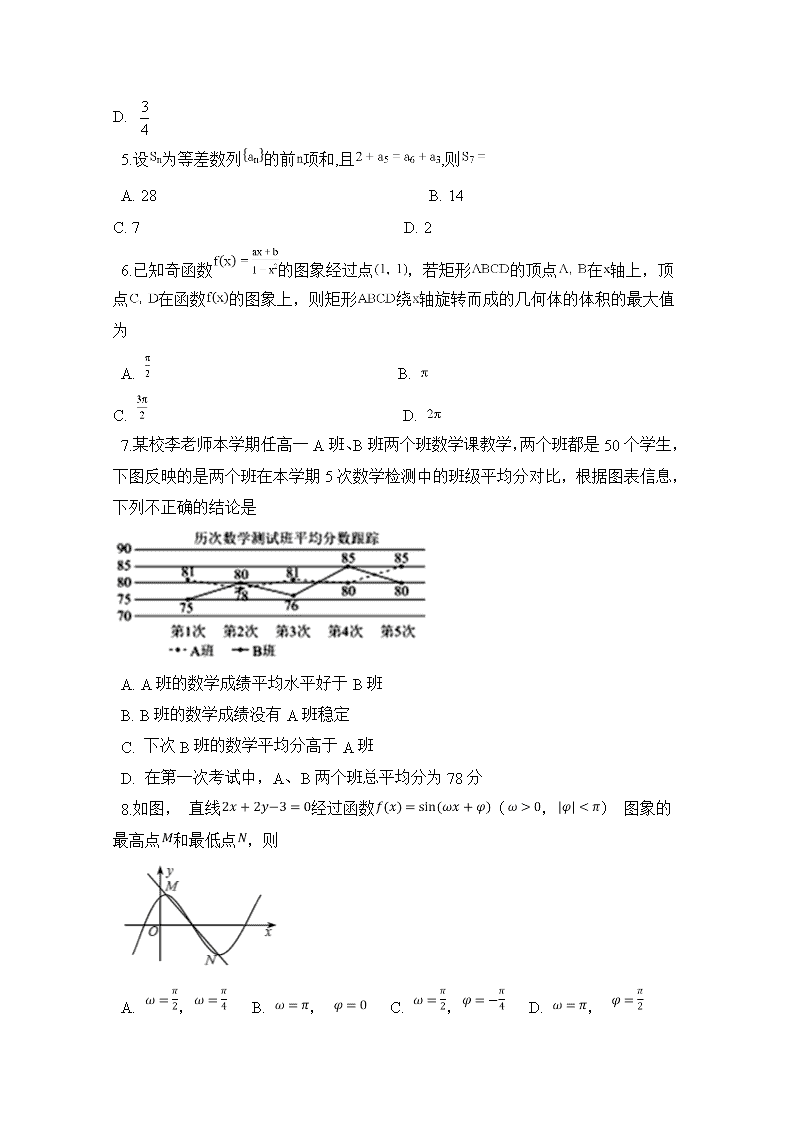
2019 一 2020 学年第二学期高三年级 6 月模拟考试 文科数学 考试时间 120 分钟 ，满分 150 分。仅在答题卷上作答。 第 I 卷 选择题（共 60 分） 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中， 只有一项是符合题目要求的。) 1.设集合 2{ | 4}A x x  ， 12 2 xB x     ，则 A B  A.  | 1 x x   B.  | 2 x x  C.  | 1 2 x x   D.  | 2 1 x x    2.设复数 z= +i（i 为虚数单位），则|z|= A. B. C. D.2 A. 2 2 B. 2 C. 2 D. 1 4.某四棱锥的三视图如图所示,则该四棱锥的体积等于 A. 1 3 B. 2 3 C. 1 2 D. 3 4 5.设 为等差数列 的前 项和,且 ,则 A. 28 B. 14 C. 7 D. 2 6.已知奇函数 的图象经过点 ，若矩形 的顶点 在 轴上，顶 点 在函数 的图象上，则矩形 绕 轴旋转而成的几何体的体积的最大值 为 A. B. C. D. 7.某校李老师本学期任高一 A 班、B 班两个班数学课教学，两个班都是 50 个学生， 下图反映的是两个班在本学期 5 次数学检测中的班级平均分对比，根据图表信息， 下列不正确的结论是 A. A 班的数学成绩平均水平好于 B 班 B. B 班的数学成绩没有 A 班稳定 C. 下次 B 班的数学平均分高于 A 班 D. 在第一次考试中，A、B 两个班总平均分为 78 分 8.如图， 直线 经过函数 （ ， ） 图象的 最高点 和最低点 ，则 A. ， B. ， C. ， D. 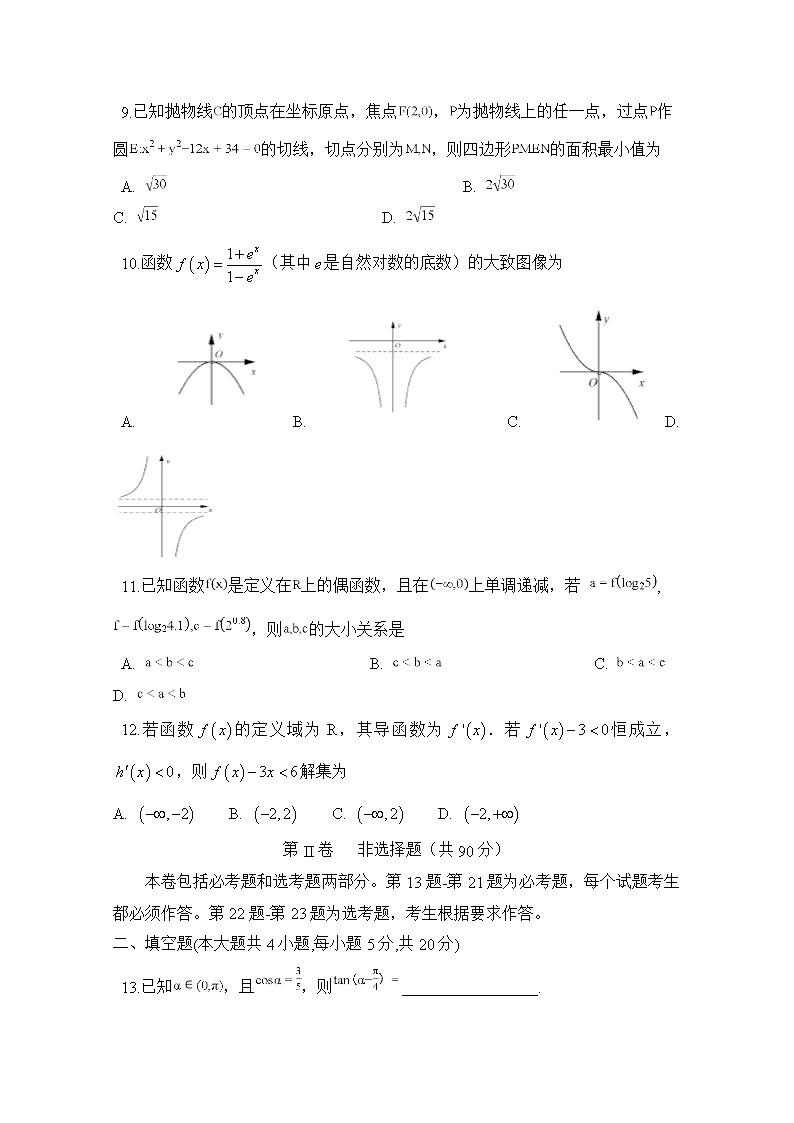， 9.已知抛物线 的顶点在坐标原点，焦点 ， 为抛物线上的任一点，过点 作 圆 的切线，切点分别为 ，则四边形 的面积最小值为 A. B. C. D. 10.函数   1 1 x x ef x e   （其中e 是自然对数的底数）的大致图像为 A. B. C. D. 11.已知函数 是定义在 上的偶函数，且在 上单调递减，若 , ，则 的大小关系是 A. B. C. D. 12.若函数  f x 的定义域为 R，其导函数为  'f x ．若  ' 3 0f x   恒成立，   0h x  ，则   3 6f x x  解集为 A.  , 2  B.  2,2 C.  ,2 D.  2,  第 II 卷 非选择题（共 90 分） 本卷包括必考题和选考题两部分。第 13 题-第 21 题为必考题，每个试题考生 都必须作答。第 22 题-第 23 题为选考题，考生根据要求作答。 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.已知 ，且 ，则 _________________. 14.若 满足 ，则 的最小值为______． 15.椭圆 的右焦点为 ，左顶点为 ，线段 的中点为 ，圆 过点 ， 且与 交于 ， 是等腰直角三角形，则圆 的标准方程是____________ 16.已知 ,  是两个不同的平面， ,m n 是两条不同的直线，有下列命题： ①若 ,m n 平行于同一平面，则 m 与n平行； ②若 m  ， / /n  ，则 m n ； ③若 ,  不平行，则在 内不存在与  平行的直线； ④若 n   ， / /m n ，则 / /m  且 / /m  ； ⑤若 / /m n ， / /  ，则m 与 所成角等于n 与  所成角. 其中真命题有__________．（填写所有正确命题的编号） 三、解答题(本大题共 6 小题,共 70 分。解答应写出文字说明、证明过程或演算步 骤。) 17. （本题 12 分） 已知数列 满足 ， ，设 ． （1）求 ， ； （2）判断数列 是否为等比数列，并说明理由； （3）求 ． 18. （本题 12 分） “黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴 都流润着浓烈的诗情.每年六、七月份，我国长江中下游地区进入持续 25 天左右的 梅雨季节，如图是江南 镇 2009～2018 年梅雨季节的降雨量（单位： ）的频率 分布直方图，试用样本频率估计总体概率，解答下列问题： “梅实初黄暮雨深”.请用样本平均数估计 镇明年梅雨季节的降雨量； “江南梅雨无限愁”. 镇的杨梅种植户老李也在犯愁，他过去种植的甲品种杨梅， 他过去种植的甲品种杨梅，亩产量受降雨量的影响较大（把握超过八成）.而乙品 种杨梅 2009～2018 年的亩产量（ /亩）与降雨量的发生频数（年）如 列联表 所示（部分数据缺失）.请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅 受降雨量影响更小？ （完善列联表，并说明理由）. 亩产量降雨量 合计 <600 2 1 合计 10 0.50 0.40 0.25 0.15 0.10 0.455 0.708 1.323 2.072 2.703 （参考公式： ，其中 ） 19. （本题 12 分） 如图，在四棱锥 中，底面 是平行四边形， ，侧面 底面 ， ， . （1）求证：面 面 ； （2）过 的平面交 于点 ，若平面 把四面体 分成体积相等的两部分， 求三棱锥 的体积. 20. （本题 12 分） 已知点 F 是抛物线 2: 2 ( 0)C x py p  的焦点，点 0 0(3, )( 1)P y y  是抛物线C 上一 点，且 13| | 4PF  ， Q 的方程为 2 2( 3) 6x y   ，过点 F 作直线l ，与抛物线C 和 Q 依次交于 M A B N， ， ， .（如图所示） （1）求抛物线C 的方程； （2）求(| | | |) | |MB NA AB  的最小值. 21. （本题 12 分） 已知函数 . (1)若 ，求函数 的单调区间； (2)若 的极小值点，求实数 a 的取值范围。 请考生在第 22、23 题中任选一题作答。注意：只能做选定的题目，如果多做， 则按所做的第一题计分，解答时请写清题号。 22. [选修 4-4：坐标系与参数方程]（本题 10 分） 在直角坐标系中，曲线C 的参数方程为 3{ 2 x cos y sin     （ 为参数），以原点为极点， x 轴的正半轴为极轴，建立极坐标系，曲线 D 的极坐标方程为 4sin 6       .  Ⅰ 写出曲线C 的极坐标的方程以及曲线 D 的直角坐标方程；  Ⅱ 若过点 2 2, 4A      （极坐标）且倾斜角为 3  的直线l 与曲线C 交于 M ， N 两 点，弦 MN 的中点为 P ，求 • AP AM AN 的值. 23.[选修 4-5：不等式选讲]（本题 10 分） 若关于 x 的不等式 3 2 3 1 0x x t     的解集为 R ，记实数t 的最大值为a . （1）求a； （2）若正实数 ,m n 满足 4 5m n a  ，求 1 4 2 3 3y m n m n    的最小值. 参考答案 1 2 3 4 5 6 7 8 9 10 11 12 C C A A B B C A D D B D 1.C【解析】因为      2 1| 4 2,2 , |2 1,2 xA x x B x            ， 所以  | 1 2 A B x x     ，选 C. 2.C【解析】复数 z= 则|z|= ． 故选：C． 3.A【解析】由题意结合a b  可设      1,0 , 0,1 , ,a b c x y    ， 则由  c a b a b       ,得|(x,y)−(1,1)|=|(1,−1)|， 据此可得：(x−1)2+(y−1)2=2， 即c 对应点的轨迹在以(1,1)为圆心的圆上， ∵圆过圆心， ∴ c 的最大值为圆的直径 2 2 ，故选：A 4.A 【解析】 抠点法，在长方体 1 1 1 1ABCD A B C D 中抠点,1.由正视图可知: 1 1C D 上没有点; 2.由侧视图可知: 1 1B C 上没有点; 3.由俯视图可知: 1CC 上没有点;4.由正（俯）视图可知: ,D E 处有点,由虚线可知 ,B F 处有点, A 点排除.由上述可还原出四棱锥 1A BEDF ,如右图 所示, 1 1 1BEDFS    , 1 1 11 13 3A BEDFV      ，故选 A . 5.B【解析】由等差数列的性质求得 ，利用等差数列的前 项和公式结合等差的性质可得 结果. 因为 ， 所以 ，故选 B. 6.B【解析】由奇函数 的图象经过点 先求出 ， 的值，得到函数表达式；接下 来分析该几何体为矩形绕 轴旋转而得，进而判断出它是一个圆柱，设其半径为 ，结合题意 即可表示出圆柱的体积，由基本不等式即可求出其最值. 由 ，及 得， ， ， ， 如图，不妨设点 在 轴的上方，不难知该旋转体为圆柱，半径 ， 令 ，整理得 ，则 为这个一元二次方程的两不等实根， 所以 于是圆柱的体积 ， 当且仅当 ，即 时， 等号成立.故选 B 7.C 【 解 析 】 A 班 的 5 次 数 学 测 试 平 均 分 分 别 为 81,80,81,80,85 ， 5 次 的 平 均 分 ，B 班的 5 次数学测试平均分分别为 75,80,76,85,80，5 次的 平均分为 ，A 班的数学平均分好于 B 班，选项 A 正确；由 于 A 班的成绩都在 80 分附近，而 B 班的平均分变化很大，所以 A 班成绩稳定些，选项 B 正 确；下次考试 A，B 班的平均分不能预料，所以选项 C 错误；在第一次考试中，总平均分为 分，选项 D 正确，故选 C. 8.A【解析】由 ， 分别是图象的最高点和最低点得其纵坐标为 1 和 ， 代入直线 得其横坐标分别为 和 ， 故 ， ，得 ，故 ，故 ， 代入 得 ， 故 ，所以 因为 ，所以 ，故选 A． 9.D【解析】设 ，则 ，进而得最值. 由题意可知抛物线的方程为 ，圆 恒的圆心为 ，半径为 ． 设 ，则 所以当 时，切线长 取得最小值 ， 此时四边形 的面积取得最小值，最小值为 ，故选 D． 10.D【解析】由题意得，函数点定义域为 x R 且 0x  ，所以定义域关于原点对称， 且     111 1 11 11 x xx x x x e eef x f xe e e              ，所以函数为奇函数，图象关于原点对称， 故选 D. 11.B【解析】由于 ，所以 .故选 B. 12.D 【解析】由已知有   3 6 0f x x   ，令     3 6g x f x x   ，则     3 0g x f x   ， 函 数  g x 在 R 单 调 递 减 ，      2 2 3 2 6 0g f        ， 由   0g x  有    2g x g  ，则 2x   ，故选 D. 13. 【解析】 ，且 ， ， .故答案为 14. 【解析】 画出约束条件 对应的平面区域如下图示： 由 ，可得 ， 将 变形为 ， 平移直线 ， 由图可知当直 经过点 时， 直线在 轴上的截距最大， 此时，目标函数 有最小值： ，故答案为 ． 15. 【解析】如图设 A（﹣a，0），可得 a＞1，c＝1，b2＝a2﹣1， 线段 AF 的中点为 B（ ，0）， 圆 F 的圆心为 F（1，0），半径 r＝|BF| ， 设 D（m，n），（m＞0，n＞0），E（m，﹣n）， 由△BDE 为等腰直角三角形，可得 kBD＝1， 即 1，即 n＝m ， 由 D 在圆 F：（x﹣1）2+y2＝（ ）2 上， 可得（m﹣1）2+（m ）2＝（ ）2， 化简可得（m﹣1）（2m﹣1+a）＝0， 解得 m＝1 或 m （舍去）， 则 n ， 将 D（1， ）代入椭圆方程，可得 1， 化简可得 a＝2 或 （舍去）， 则圆 F 的标准方程为（x﹣1）2+y2 ， 故答案为：（x﹣1）2+y2 ． 16.②⑤ 【解析】① m n， 还可以相交或异面；③若 ， 不平行，则 ， 相交，设 l   ，在 内 存在直线 a ，使得 / /a l ，则 / /a  ；④ m 还可能在平面 内或平面  内． ②⑤正确. 17.（ 1 ） ， ；（ 2 ）是等比数列，理由详见解析；（ 3 ） .【解析】 数列 满足 ， ， 当 时， ， 解得： ． 当 时， 解得： ． 当 时， ， 所以： ． 则数列 为以 2 为首项，2 为公比的等比数列． 由 和 得： ， 所以： ， ， ， ． 18. 乙 【解析】 频率分布直方图中第四组的频率为 . 所以用样本平均数估计 镇明年梅雨季节的降雨量为 . 根据频率分布直方图可知，降雨量在 200～400 之间的频数为 . 进而完善列联表如图. 亩产量降雨量 200～400 之间 200～400 之外 合计 <600 2 2 4 5 1 6 合计 7 3 10 . 故认为乙品种杨梅的亩产量与降雨量有关的把握不足 75%. 而甲品种杨梅降雨量影响的把握超过八成，故老李来年应该种植乙品种杨梅. 19.（1）证明：因为 ，则 ， 又侧面 底面 ， 面 面 ， 面 ， 则 面 面 ，则 又因为 ， 为平行四边形， 则 ，又 则 为等边三角形，则 为菱形， 则 又 ，则 面 ， 面 ，则面 面 （2）由平面 把四面体 分成体积相等的两部分，则 为 中点 由 ， ，得 由 知 为菱形，则 又由 知 面 ，则 则 则 20.（1） yx 42  ；（2） 828  ． 【解析】 ）（1 由  0y3，P 在抛物线C 上得 9p2 0 y ， 又由 4 13|PF|  得 4 13 2y0  p ， 解得      2 9 1y0 p ，      2 4 9 0 p y ，又 10 y ，故      2 4 9 0 p y . 所以抛物线C 的方程为 yx 42  .………………4 分 ）（2 由题知直线的斜率l 一定存在，设直线l 的方程为 1 kxy . 则圆心  3,0Q 到直线l 的距离为 1 2 2   k d ，  1 4622|| 2 22  kdrAB .………………6 分 设  11, yxM ，  22, yxN ， 由      1 42 kxy yx 得   0142 22  yky ， 则 24 2 21  kyy ，由抛物线定义知 )1(42|| 2 21 kyyMN  ，………………8 分  |||)|(| ABNAMB  |||)||(| ABABMN  2|||||| ABABMN  ） 1 46(4)1 46()1(8 22 2  kkk 241 16)1(41k68 2 22  kk）（ .………………10 分 设 12  kt ）（ 1t  ， 则 |||)||(| ABNAMB  24164t68 2  tt 2416 3 2)3 1-t(68 2  t ， ）（ 1t  ， 函数 ty 16y3 2)3 1-t(6 2  和 在 ,1 上都是单调递增函数， 当 1t  时即 0k 时， |||)||(| ABMAMB  有最小值 828  .………………12 分 21.（1）单调减区间为 ，单调增区间为 （2） 【解析】（1）由题 由 ，得 由 ，得 ；由 ，得 的单调减区间为 ，单调增区间为 （2） ， 因为 是 的极小值点，所以 ，即 ， 所以 1°当 时， 在 上单调递减； 在 上单调递增； 所以 是 的极小值点，符合题意； 2°当 时， 在 上单调递增； 在 上单调递减； 在 上单调递增； 所以 是 的极小值点，符合题意； 3°当 时， 在 上单调递增， 无极值点，不合题意 4°当 时， 在 上单调递增； 在 上单调递减； 在 上单调递增； 所以 是 的极大值点，不符合题意； 综上知，所求 的取值范围为 22.(Ⅰ)曲线 C 的极坐标方程为： 2 2 2 2cos sin 19 4      ；曲线 D 的直角坐标方程为： 2 2x y 2 3 2y x  .(Ⅱ) 4 19 3 16  . 【解析】  Ⅰ 由题意C 的方程为： 3 ,{ 2 , x cos y sin     可得 C 的普通方程为： 2 2 19 4 x y  ， 将 ,{ , x cos y sin       代入曲线方程可得： 2 2 2 2cos sin 19 4      . 因为曲线 D 的极坐标方程为 4sin 6       ， 所以 2 3 14 sin 4 sin cos6 2 2                   . 又 2 2 2x y   ， cosx   ， siny   . 所以 2 2 2 3 2x y y x   . 所以曲线 C 的极坐标方程为： 2 2 2 2cos sin 19 4      ；曲线 D 的直角坐标方程为： 2 2x y 2 3 2y x  .  Ⅱ 因为点 2 2, 4A      ，化为直角坐标为 2 2 2,4{ 2 2 2,2 x cos y sin       所以  2,2A . 因为直线l 过点  2,2A 且倾斜角为 3  ，所以直线l 的参数方程为 12 ,2{ 32 ,2 x t y t     （t 为参数）， 代入 2 2 19 4 x y  中可得：  231 8 18 3 16 04 t t    ， 所以由韦达定理： 1 2 32 72 3 31 bt t a      ， 1 2 64 31 ct t a   ， 所以 1 2 1 2 4 19 32 • 16 t t AP AM AN t t    . 23.（1） 3a  （2）3 解析：（1）因为 3 2 3 1 0x x t     ，所以 3 2 3 1 1x x    ， 又因为    3 2 3 1 3 2 1 3 3x x x x        ，所以 3t  ， 从而实数t 的最大值 3a  . （2）因为      1 4 1 44 5 2 3 32 3 3 2 3 3m n m n m nm n m n m n m n                        2 1 42 3 3 92 3 3m n m nm n m n             ， 所以 1 43 92 3 3m n m n       ，从而 3y  ， 当且仅当 1 4 2 3 3m n m n   ，即 1 3m n  时等号成立， 所以 1 4 2 3 3y m n m n    的最小值为3.