- 411.00 KB
- 2021-06-23 发布
2016-2017学年福建省泉州市南安市柳城中学高二(下)第一次月考数学试卷
一、选择题(本大题共12小题,每小题5分,共60分
1.已知f(x)=xln x,若f′(x0)=2,则x0等于( )
A.e2 B.e C. D.ln 2
2.对任意的x,有f′(x)=4x3,f(1)=﹣1,则此函数解析式( )
A.f(x)=x3 B.f(x)=x4﹣2 C.f(x)=x3+1 D.f(x)=x4﹣1
3.下列求导运算正确的是( )
A.(x+)′=1+ B.(log2x)′=
C.(3x)′=3xlog3e D.(x2cosx)′=﹣2xsinx
4.曲线y=cosx(0≤x≤)与坐标轴围成的面积是( )
A.4 B. C.3 D.2
5.函数f(x)=x﹣lnx的单调递减区间是( )
A.(0,1) B.(0,+∞) C.(1,+∞) D.(﹣∞,0)∪(1,+∞)
6.若函数f(x)=ax4+bx2+c满足f′(1)=2,则f′(﹣1)=( )
A.﹣1 B.﹣2 C.2 D.0
7.函数f(x)=x3﹣3x(﹣1<x<1)( )
A.有最大值,但无最小值 B.有最大值,也有最小值
C.无最大值,也无最小值 D.无最大值,但有最小值
8.某公司生产一种产品,固定成本为20000元,每生产一单位的产品,成本增加100元,若总收入R与年产量x的关系是R(x)=,则当总利润最大时,每年生产产品的单位数是( )
A.150 B.200 C.250 D.300
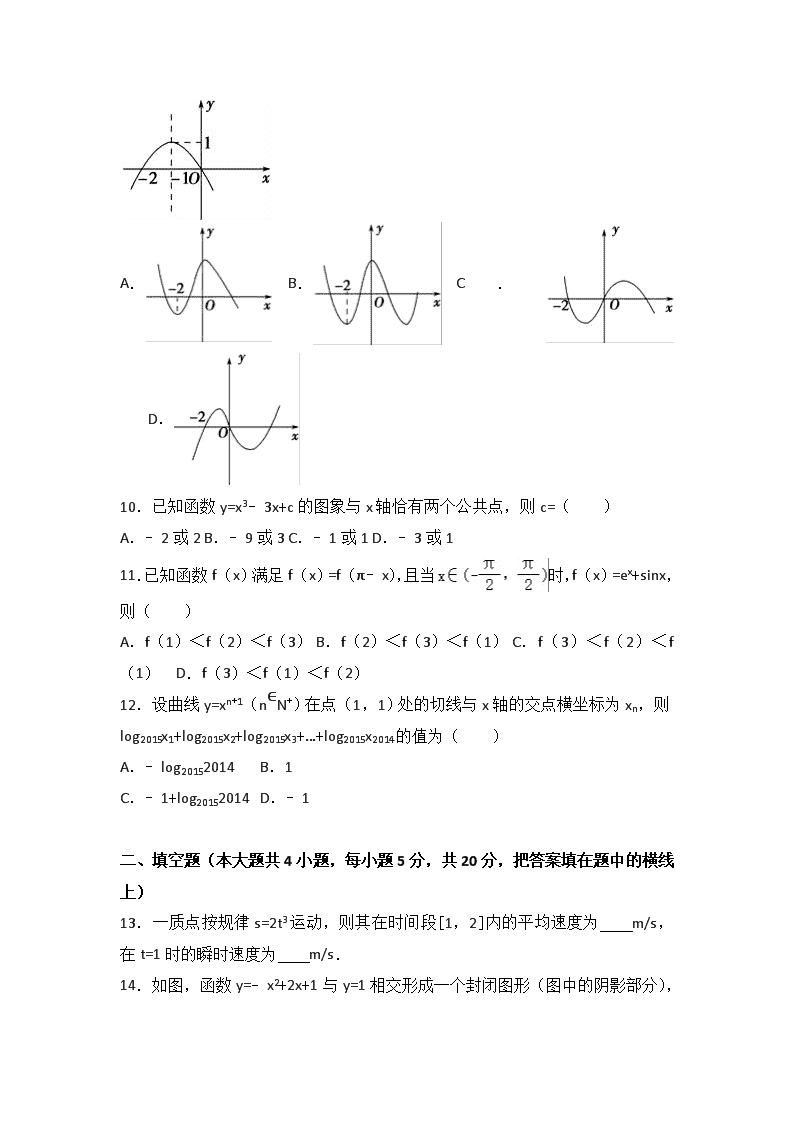
9.已知f(x)的导函数f'(x)图象如图所示,那么f(x)的图象最有可能是图中的( )
A. B. C. D.
10.已知函数y=x3﹣3x+c的图象与x轴恰有两个公共点,则c=( )
A.﹣2或2 B.﹣9或3 C.﹣1或1 D.﹣3或1
11.已知函数f(x)满足f(x)=f(π﹣x),且当时,f(x)=ex+sinx,则( )
A.f(1)<f(2)<f(3) B.f(2)<f(3)<f(1) C.f(3)<f(2)<f(1) D.f(3)<f(1)<f(2)
12.设曲线y=xn+1(n∈N+)在点(1,1)处的切线与x轴的交点横坐标为xn,则log2015x1+log2015x2+log2015x3+…+log2015x2014的值为( )
A.﹣log20152014 B.1
C.﹣1+log20152014 D.﹣1
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.一质点按规律s=2t3运动,则其在时间段[1,2]内的平均速度为 m/s,在t=1时的瞬时速度为 m/s.
14.如图,函数y=﹣x2+2x+
1与y=1相交形成一个封闭图形(图中的阴影部分),则该封闭图形的面积是 .
15.函数y=x3+ax2+x在R上是增函数,则a的取值范围是 .
16.已知函数f(x)=﹣2x2+lnx(a>0).若函数f(x)在[1,2]上为单调函数,则a的取值范围是 .
三、解答题(本大题共6小题,共60分,解答题影写出文字说明,证明过程或演算步骤)
17.计算下列定积分.
(1)
(2)设,则.
18.已知曲线y=x3,
(1)求曲线在点P(2,f(2))处的切线方程;
(2)求曲线过点P(2,f(x))的切线方程.
19.设函数f(x)=lnx+ln(2﹣x)+ax(a>0).
(1)当a=1时,求f(x)的单调区间.
(2)若f(x)在(0,1]上的最大值为,求a的值.
20.某公司在甲、乙两地销售同一种品牌的汽车,利润(单位:万元)分别为L1=5.06x﹣0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,求该公司能获得的最大利润为多少万元?
21.已知函数f(x)=x3+ax2+bx+c在x=﹣1与x=2处都取得极值.
(Ⅰ)求a,b的值及函数f(x)的单调区间;
(Ⅱ)若对x∈[﹣2,3],不等式f(x)+c<c2恒成立,求c的取值范围.
22.已知a,b是实数,函数f(x)=x3+ax,g(x)=x2+bx,f′(x)和g′(x)是f(x),g(x)的导函数,若f′(x)g′(x)≥0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性一致
(1)设a>0,若函数f(x)和g(x)在区间[﹣1,+∞)上单调性一致,求实数b的取值范围;
(2)设a<0,且a≠b,若函数f(x)和g(x)在以a,b为端点的开区间上单调性一致,求|a﹣b|的最大值.
2016-2017学年福建省泉州市南安市柳城中学高二(下)第一次月考数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,每小题5分,共60分
1.已知f(x)=xln x,若f′(x0)=2,则x0等于( )
A.e2 B.e C. D.ln 2
【考点】导数的运算.
【分析】先对函数进行求导,然后根据f′(x0)=2,建立等式关系,解之即可求得答案.
【解答】解:∵f(x)=xln x,(x>0)
∴f′(x)=lnx+1,
∵f′(x0)=2,
∴f′(x0)=lnx0+1=2,
解得x0=e,
∴x0的值等于e.
故选:B.
2.对任意的x,有f′(x)=4x3,f(1)=﹣1,则此函数解析式( )
A.f(x)=x3 B.f(x)=x4﹣2 C.f(x)=x3+1 D.f(x)=x4﹣1
【考点】导数的运算.
【分析】根据导数的运算法则,求出导数的原函数为f(x)=x4+c(c为常数),代入值计算即可得到c的值.
【解答】解:∵f′(x)=4x3,
∴f(x)=x4+c(c为常数),
∵f(1)=﹣1,
∴1+c=﹣1,
∴c=﹣2,
∴f(x)=x4﹣2,
故选:B.
3.下列求导运算正确的是( )
A.(x+)′=1+ B.(log2x)′=
C.(3x)′=3xlog3e D.(x2cosx)′=﹣2xsinx
【考点】导数的运算.
【分析】由导数的运算法则逐个选项验证可得.
【解答】解:选项A,(x+)′=1﹣,故错误;
选项B,(log2x)′=,故正确;
选项C,(3x)′=3xln3,故错误;
选项D,(x2cosx)′=2xcosx﹣x2sinx,故错误.
故选:B
4.曲线y=cosx(0≤x≤)与坐标轴围成的面积是( )
A.4 B. C.3 D.2
【考点】余弦函数的图象.
【分析】由条件利用余弦函数的图象的对称性,定积分的意义,可得曲线y=cosx(0≤x≤)与坐标轴围成的面积是3=3sinx,计算求的结果.
【解答】解:由条件利用余弦函数的图象的对称性可得曲线y=cosx(0≤x≤)与坐标轴围成的面积是3=3sinx=3,
故选:C.
5.函数f(x)=x﹣lnx的单调递减区间是( )
A.(0,1) B.(0,+∞) C.(1,+∞) D.(﹣∞,0)∪(1,+∞)
【考点】利用导数研究函数的单调性.
【分析】求出函数的导数为y′,再解y'<0得x的范围.结合函数的定义域,即可得到单调递减区间.
【解答】解:函数y=x﹣lnx的导数为y=1﹣,
令y′=1﹣<0,得x<1
∴结合函数的定义域,得当x∈(0,1)时,函数为单调减函数.
因此,函数y=x﹣lnx的单调递减区间是(0,1)
故选:A.
6.若函数f(x)=ax4+bx2+c满足f′(1)=2,则f′(﹣1)=( )
A.﹣1 B.﹣2 C.2 D.0
【考点】导数的运算.
【分析】根据导数的运算法则先求导,再判断其导函数为奇函数,问题得以解决
【解答】解:∵f(x)=ax4+bx2+c,
∴f′(x)=4ax3+2bx,
∴f′(﹣x)=﹣4ax3﹣2bx=﹣f′(x),
∴f′(﹣1)=﹣f′(1)=﹣2,
故选:B.
7.函数f(x)=x3﹣3x(﹣1<x<1)( )
A.有最大值,但无最小值 B.有最大值,也有最小值
C.无最大值,也无最小值 D.无最大值,但有最小值
【考点】利用导数研究函数的极值.
【分析】求出函数的导数,判断函数的单调性,然后推出结果.
【解答】解:函数f(x)=x3﹣3x(﹣1<x<1),
可得f′(x)=3x2﹣3,令3x2﹣3=0,可得x=±1,
±1∉(﹣1,1),x∈(﹣1,1),f(x)<0.
函数f(x)=x3﹣3x(﹣1<x<1)是减函数,没有最值.
故选:C.
8.某公司生产一种产品,固定成本为20000元,每生产一单位的产品,成本增加100元,若总收入R与年产量x的关系是R(x)=,则当总利润最大时,每年生产产品的单位数是( )
A.150 B.200 C.250 D.300
【考点】函数的最值及其几何意义.
【分析】先根据“利润=收入﹣成本”列出总利润关于x的函数表达式,由题意这是一个分段函数,再分别求出当0≤x≤390,及x>390时的总利润的最大值,通过比较得到整个函数的最大值.
【解答】解:由题意当年产量为x时,总成本为20000+100x,
又总收入R与年产量x的关系是R(x)=,
∴总利润Q(x)=,即Q(x)=
①当0≤x≤390时,Q′(x)=﹣,令Q′(x)=0得x=300,
由Q′(x)<0得300<x≤390,此时Q(x)是减函数,
由Q′(x)>0得0<x<300,此时Q(x)是增函数,
∴当0≤x≤390时,Q(x)max=Q;
②当x>390时,Q(x)=﹣100x+70090是减函数,∴Q(x)<Q;
∴当x=300时,Q(x)的最大值为40000.
故选D
9.已知f(x)的导函数f'(x)图象如图所示,那么f(x)的图象最有可能是图中的( )
A. B. C. D.
【考点】函数的图象.
【分析】先根据导函数的图象确定导函数大于0
的范围和小于0的x的范围,进而根据当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减确定原函数的单调增减区间.
【解答】解:x<﹣2时,f′(x)<0,则f(x)单减;
﹣2<x<0时,f′(x)>0,则f(x)单增;
x>0时,f′(x)<0,则f(x)单减.
则符合上述条件的只有选项A.
故选A.
10.已知函数y=x3﹣3x+c的图象与x轴恰有两个公共点,则c=( )
A.﹣2或2 B.﹣9或3 C.﹣1或1 D.﹣3或1
【考点】利用导数研究函数的极值;函数的零点与方程根的关系.
【分析】求导函数,确定函数的单调性,确定函数的极值点,利用函数y=x3﹣3x+c的图象与x轴恰有两个公共点,可得极大值等于0或极小值等于0,由此可求c的值.
【解答】解:求导函数可得y′=3(x+1)(x﹣1),
令y′>0,可得x>1或x<﹣1;令y′<0,可得﹣1<x<1;
∴函数在(﹣∞,﹣1),(1,+∞)上单调增,(﹣1,1)上单调减,
∴函数在x=﹣1处取得极大值,在x=1处取得极小值.
∵函数y=x3﹣3x+c的图象与x轴恰有两个公共点,
∴极大值等于0或极小值等于0.
∴1﹣3+c=0或﹣1+3+c=0,
∴c=﹣2或2.
故选:A.
11.已知函数f(x)满足f(x)=f(π﹣x),且当时,f(x)=ex+sinx,则( )
A.f(1)<f(2)<f(3) B.f(2)<f(3)<f(1) C.f(3)<f(2)<f(1) D.f(3)<f(1)<f(2)
【考点】正弦函数的对称性;函数的值;正弦函数的单调性.
【分析】根据函数的对称性和函数的单调性即可比较大小.
【解答】解:∵f(x)=f(π﹣x),则f(x)关于x=对称
∴f(3)=f(π﹣3),f(2)=f(π﹣2)
当时,y=ex+y=sinx,单调递增,
∴此时函数f(x)=ex+sinx是增函数.
∵0<π﹣3<1<π﹣2,
∴f(π﹣3)<f(1)<f(π﹣2),
即f(3)<f(1)<f(2).
故选:D.
12.设曲线y=xn+1(n∈N+)在点(1,1)处的切线与x轴的交点横坐标为xn,则log2015x1+log2015x2+log2015x3+…+log2015x2014的值为( )
A.﹣log20152014 B.1
C.﹣1+log20152014 D.﹣1
【考点】利用导数研究曲线上某点切线方程.
【分析】要求log2015x1+log2015x2+…+log2015x2014,需求x1•x2•…•x2014的值,只须求出切线与x轴的交点的横坐标即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
【解答】解:对y=xn+1(n∈N*)求导,得y′=(n+1)xn,
令x=1得在点(1,1)处的切线的斜率k=n+1,在点
(1,1)处的切线方程为y﹣1=k(xn﹣1)=(n+1)(xn﹣1),
不妨设y=0,可得xn=,
则x1•x2•x3…•xn=••…•=,
从而log2015x1+log2015x2+…+log2015x2014
=log2015(x1•x2…x2014)
=log2015=﹣1..
故选:D.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)
13.一质点按规律s=2t3运动,则其在时间段[1,2]内的平均速度为 14 m/s,在t=1时的瞬时速度为 6 m/s.
【考点】变化的快慢与变化率.
【分析】根据平均速度的求解公式平均速度=位移÷时间,建立等式关系即可,利用导数的物理意义即可得出.
【解答】解:在时间段[1,2]内的平均速度为=14,
v(t)=s′=6t2,
把t=1代入可得t=1时的瞬时速度为v(1)=s′=6,
故答案为:14,6.
14.如图,函数y=﹣x2+2x+1与y=1相交形成一个封闭图形(图中的阴影部分),则该封闭图形的面积是 .
【考点】定积分.
【分析】本题考查的知识点是定积分的几何意义,首先我们要联立两个曲线的方程,判断他们的交点,以确定积分公式中x的取值范围,再根据定积分的几何意义,所求图形的面积为S=∫02(﹣x2+2x+1)dx﹣∫021dx,计算后即得答案.
【解答】解:函数y=﹣x2+2x+1与y=1的两个交点为(0,1)和(2,1),
所以封闭图形的面积等于S=∫02(﹣x2+2x+1)dx﹣∫021dx
=∫02(﹣x2+2x+1﹣1)dx
=∫02(﹣x2+2x)dx
=(﹣+x2)|=﹣+4=.
故答案为:
15.函数y=x3+ax2+x在R上是增函数,则a的取值范围是 ﹣≤a≤ .
【考点】利用导数研究函数的单调性.
【分析】问题转化为y′=3x2+2ax+1≥0在R上恒成立,结合二次函数的性质得到不等式,解出即可.
【解答】解:若函数y=x3+ax2+x在R上是增函数,
则只需y′=3x2+2ax+1≥0在R上恒成立,
∴只需△=4a2﹣12≤0即可,
解得:﹣≤a≤,
故答案为:﹣≤a≤.
16.已知函数f(x)=﹣2x2+lnx(a>0).若函数f(x)在[1,2]上为单调函数,则a的取值范围是 (0,]∪[1,+∞) .
【考点】利用导数研究函数的单调性.
【分析】求出原函数的导函数,由函数f(x)在[1,2]上为单调函数,得到x∈[1,2]时,f′(x)=≥0恒成立,或f′(x)=≤0恒成立,分离参数a后引入新的辅助函数h(x)=4x﹣,由单调性求得其在[1,2]上的最值得答案.
【解答】解:由f(x)=﹣2x2+lnx,得f′(x)=,
∵函数f(x)在区间[1,2]上为单调函数,
∴x∈[1,2]时,f′(x)=≥0恒成立,或f′(x)=≤0恒成立,
即对x∈[1,2]恒成立,或对x∈[1,2]恒成立.
设h(x)=4x﹣,
∵函数h(x)在[1,2]上单调递增,
∴h(2)=4×2﹣=①,或②.
解①得,0<a≤,解②得,a≥1.
∴a的取值范围是(0,]∪[1,+∞).
故答案为:(0,]∪[1,+∞).
三、解答题(本大题共6小题,共60分,解答题影写出文字说明,证明过程或演算步骤)
17.计算下列定积分.
(1)
(2)设,则.
【考点】定积分.
【分析】(1)根据绝对值函数,分段求出定积分即可,
(2)根据分段函数,分别求出定积分即可.
【解答】解:(1)=(x+1)dx+(﹣x﹣1)dx,
=(x2+x)|﹣(x2+x)|,
=2+2﹣+1﹣(﹣1﹣+3),
=;
(2)设,
则=x2dx+(2﹣x)dx,
=x3|+(2x﹣x2)|,
=+(4﹣2)﹣(2﹣),
=.
18.已知曲线y=x3,
(1)求曲线在点P(2,f(2))处的切线方程;
(2)求曲线过点P(2,f(x))的切线方程.
【考点】利用导数研究曲线上某点切线方程.
【分析】(1)求出函数的导数,可得在x=2处切线的斜率,求出切点,由点斜式方程可得切线的方程;
(2)设切点坐标为(x0, x03),求得切线的斜率,运用点斜式方程求得切线方程,代入点P,解方程可得切点的横坐标,可得切线的斜率和切线方程.
【解答】解:(1)y=x3,导数y′=x2,
曲线在点P(2,f(2))处的切线斜率为4,
切点为(2,),
可得曲线在点P(2,f(2))处的切线方程为y﹣=4(x﹣2),
12x﹣3y﹣16=0;
(2)设过点P(2,)的直线与曲线相切,
切点坐标为(x0, x03),
所以切线的斜率为,
所以切线方程为,
因为切线过点P(2,),
所以,
解得x0=2或x0=﹣1,
当x0=2时,切线方程为12x﹣3y﹣16=0;
当x0=﹣1时,切线方程为3y﹣3x﹣2=0.
所以所求切线方程为12x﹣3y﹣16=0或3x﹣3y+2=0.
19.设函数f(x)=lnx+ln(2﹣x)+ax(a>0).
(1)当a=1时,求f(x)的单调区间.
(2)若f(x)在(0,1]上的最大值为,求a的值.
【考点】利用导数研究函数的单调性.
【分析】(1)已知a=1,f′(x)=﹣+1,求解f(x)的单调区间,只需令f′(x)>0解出单调增区间,令f′(x)<0解出单调减区间.
(2)区间(0,1]上的最值问题,通过导数得到单调性,结合极值点和端点的比较得到,确定待定量a的值.
【解答】解:对函数求导得:,定义域为(0,2)
(1)当a=1时,f′(x)=﹣+1,
当f′(x)>0,即0<x<时,f(x)为增函数;当f′(x)<0,<x<2时,f(x)为减函数.
所以f(x)的单调增区间为(0,),单调减区间为(,2)
(2)函数f(x)=lnx+ln(2﹣x)+ax(a>0).
因为a>0,x∈(0,1],所以>0,所以函数为单调增函数,(0,1]为单调递增区间.
最大值在右端点取到.
所以a=.
20.某公司在甲、乙两地销售同一种品牌的汽车,利润(单位:万元)分别为L1=5.06x﹣0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,求该公司能获得的最大利润为多少万元?
【考点】函数模型的选择与应用.
【分析】先根据题意,设甲销售x辆,则乙销售(15﹣x)辆,再列出总利润y的表达式,是一个关于x的二次函数,最后求此二次函数的最大值即可.
【解答】解:设甲地销售x辆,则乙地销售15﹣x辆,0≤x≤15,
则该公司能获得的最大利润y=5.06x﹣0.15x2+2(15﹣x)=﹣0.15x2+3.06x+30,
当x=10.2时,S取最大值
又x必须是整数,故x=10,此时Smax=45.6(万元).
即甲地销售10辆,则乙地销售5辆时,该公司能获得的最大利润为45.6万元
21.已知函数f(x)=x3+ax2+bx+c在x=﹣1与x=2处都取得极值.
(Ⅰ)求a,b的值及函数f(x)的单调区间;
(Ⅱ)若对x∈[﹣2,3],不等式f(x)+c<c2恒成立,求c的取值范围.
【考点】利用导数研究函数的极值;利用导数研究函数的单调性;不等式的证明.
【分析】(1)求出f′(x)并令其=0得到方程,把x=﹣1和x=2代入求出a、b即可;
(2)求出函数的最大值为f(﹣1),要使不等式恒成立,既要证f(﹣1)+c<c2,即可求出c的取值范围.
【解答】解:(Ⅰ)f′(x)=3x2+2ax+b,
由题意:即
解得
∴,f′(x)=3x2﹣3x﹣6
令f′(x)<0,解得﹣1<x<2;
令f′(x)>0,解得x<﹣1或x>2,
∴f(x)的减区间为(﹣1,2);增区间为(﹣∞,﹣1),(2,+∞).
(Ⅱ)由(Ⅰ)知,f(x)在(﹣∞,﹣1)上单调递增;
在(﹣1,2)上单调递减;在(2,+∞)上单调递增.
∴x∈[﹣2,3]时,f(x)的最大值即为f(﹣1)与f(3)中的较大者.;
∴当x=﹣1时,f(x)取得最大值.
要使,只需,即:2c2>7+5c
解得:c<﹣1或.
∴c的取值范围为.
22.已知a,b是实数,函数f(x)=x3+ax,g(x)=x2+bx,f′(x)和g′(x)是f(x),g(x)的导函数,若f′(x)g′(x)≥0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性一致
(1)设a>0,若函数f(x)和g(x)在区间[﹣1,+∞)上单调性一致,求实数b的取值范围;
(2)设a<0,且a≠b,若函数f(x)和g(x)在以a,b为端点的开区间上单调性一致,求|a﹣b|的最大值.
【考点】利用导数研究函数的单调性.
【分析】(1)先求出函数f(x)和g(x)的导函数,再利用函数f(x)和g(x)在区间[﹣1,+∞)上单调性一致即f′(x)g′(x)≥0在[﹣1,+∞)上恒成立,以及3x2+a>0,来求实数b的取值范围;
(2)先求出f′(x)=0的根以及g′(x)=0的根,再分别求出两个函数的单调区间,综合在一起看何时函数f(x)和g(x)在以a,b为端点的开区间上单调性一致,进而求得|a﹣b|的最大值.
【解答】解:f′(x)=3x2+a,g′(x)=2x+b.
(1)由题得f′(x)g′(x)≥0在[﹣1,+∞)上恒成立.因为a>0,故3x2+a>0,
进而2x+b≥0,即b≥﹣2x在[﹣1,+∞)上恒成立,所以b≥2.
故实数b的取值范围是[2,+∞)
(2)令f′(x)=0,得x=.
若b>0,由a<0得0∈(a,b).又因为f′(0)g′(0)=ab<0,
所以函数f(x)和g(x)在(a,b)上不是单调性一致的.
因此b≤0.
现设b≤0,当x∈(﹣∞,0)时,g′(x)<0;
当x∈(﹣∝,﹣)时,f′(x)>0.
因此,当x∈(﹣∝,﹣)时,f′(x)g′(x)<0.故由题设得a≥﹣且b≥﹣,
从而﹣≤a<0,于是﹣<b≤0,因此|a﹣b|≤,且当a=﹣,b=0时等号成立,
又当a=﹣,b=0时,f′(x)g′(x)=6x(x2﹣),从而当x∈(﹣,0)时f′(x)g′(x)>0.
故函数f(x)和g(x)在(﹣,0)上单调性一致,因此|a﹣b|的最大值为.
2017年5月17日
【来.源:全,品…中&高*考*网】