- 1.13 MB
- 2021-06-23 发布
绝密★启封前
2017全国卷Ⅲ高考压轴卷
文科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
注意事项:
1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上。考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。 2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答,答案无效。
3.考试结束,监考员将试题卷、答题卡一并收回。
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知全集且则等于
(A) (B) (C) (D)
2.已知(为虚数单位),则的共轭复数的虚部为( )
(A) (B) (C) (D)
3袋中有五张卡片,其中红色卡片三张,标号分别为,蓝色卡片两张,标号分别为,从以上五张卡片中任取两张,则这两张卡片颜色不同且标号之和不小于的概率为
(A) (B) (C) (D)
4.在射击训练中,某战士射击了两次,设命题是“第一次射击击中目标”,命题是“第二次射击击中目标”,则命题“两次射击中至少有一次没有击中目标”为真命题的充要条件是()
A.为真命题 B.为真命题
C. 为真命题 D.为真命题
5.设是等差数列的前项和,若,则=()
(A) (B) (C) (D)
4
4
2
1
4
2
正视图
侧视图
俯视图
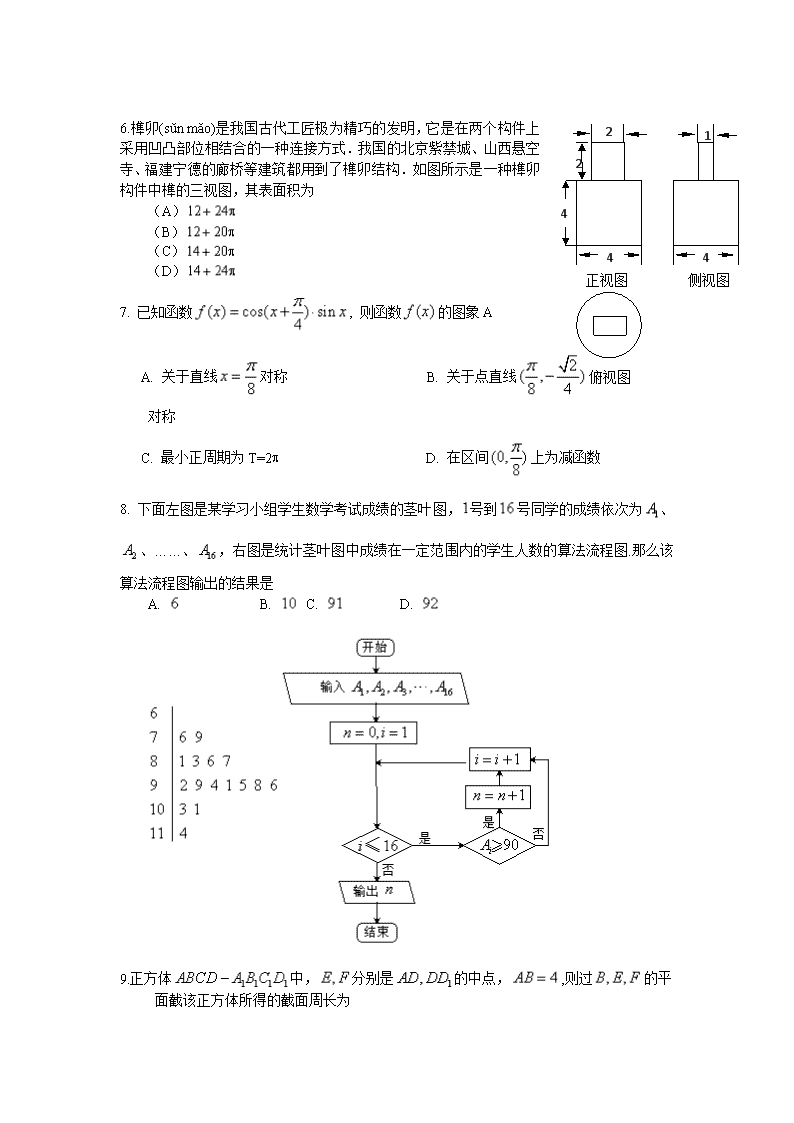
6.榫卯(sŭn măo)是我国古代工匠极为精巧的发明,它是在两个构件上采用凹凸部位相结合的一种连接方式.我国的北京紫禁城、山西悬空寺、福建宁德的廊桥等建筑都用到了榫卯结构.如图所示是一种榫卯构件中榫的三视图,其表面积为
(A)
(B)
(C)
(D)
7. 已知函数, 则函数的图象A
A. 关于直线对称 B. 关于点直线对称
C. 最小正周期为T=2p D. 在区间上为减函数
8. 下面左图是某学习小组学生数学考试成绩的茎叶图,号到号同学的成绩依次为、、……、,右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图.那么该算法流程图输出的结果是
A. B. C. D.
9.正方体中,分别是的中点,,则过的平面截该正方体所得的截面周长为
(A)(B)
(C)(D)
10.已知是定义在上的奇函数,且时,,
则函数(为自然对数的底数)的零点个数是()
A. B. C. D.
11.等差数列前项和为,已知
,则
A. B.
C. D.
12. 若是双曲线的右焦点,过作该双曲线一条渐近线的垂线与两条渐近线交于两点,为坐标原点,的面积为 ,则该双曲线的离心率
A. B. C. D.
第Ⅱ卷
注意事项:
须用黑色墨水签字笔在答题卡上作答。若在试卷上作答,答案无效。
本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须作答。第22题~ 第23题为选考题,考生根据要求做答。
二.填空题:本大题共4小题,每小题5分
13.已知平面向量a,b满足|a|=,|b|=2,a·b=-3,则|a+2b|=
14.数列的前项和为,且,,则数列的通项公式为________.
15.已知直线是圆的对称轴,过点作圆的一条切线,切点为,则
16.设函数.有下列五个命题:
①若对任意,关于的不等式恒成立,则;
②若存在,使得不等式成立,则;
③若对任意及任意不等式恒成立,则;
④若对任意,存在,使得不等式成立,则;
⑤若存在及,使得不等式成立,则.
其中,所有正确结论的序号为______.
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知的内角,,的对边分别为,,,若,
,且.
(1)求角的值;
(2)若,,,求.
(18)(本小题满分12分)
某渔业公司为了解投资收益情况,调查了旗下的养鱼场和远洋捕捞队近10个月的利润情况.根据所收集的数据得知,近10个月总投资养鱼场一千万元,获得的月利润频数分布表如下:
月利润(单位: 千万元)
-0.2
-0.1
0
0.1
0.3
频数
2
1
2
4
1
近10个月总投资远洋捕捞队一千万元,获得的月利润频率分布直方图如下:
频率/组距
月利润(千万元)
-0.4
0.5
0
0.2
0.4
0.6
1
1.5
-0.2
(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼场的资金为千万元,投资远洋捕捞队的资金为千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
19. (本小题满分12分)
如图,在几何体中,四边形是菱形,平面, ,且.
(1)证明:平面平面.
(2)若,求几何体的体积.
20. (本小题满分12分)
已知抛物线的焦点坐标为,过的直线交抛物线于两点,直线分别与直线:相交于两点.
(Ⅰ)求抛物线的方程;
(Ⅱ)证明△ABO与△MNO的面积之比为定值.
(本小题满分12分)已知函数
(I)若函数φ (x) = f (x)-,求函数φ (x)的单调区间;
(II)设直线l为函数f (x)的图象上一点A(x0,f (x0))处的切线,在区间(1,+∞)上是否存在使得直线l与曲线y=g(x)相切若存在,求出的个数;若不存在,请说明理由。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分,解答时请写清题号.
22.选修4-4:坐标系与参数方程
在直角坐标系中,曲线的参数方程为,(其中为参数),曲线,以原点为极点,轴的正半轴为极轴建立极坐标系,射线与曲线分别交于点(均异于原点)
(1)求曲线的极坐标方程;
(2)当时,求的取值范围.
23.选修4-5:不等式选讲
已知函数
(1)若不等式恒成立,求实数的最大值;
(2)当时,函数有零点,求实数的取值范围.
2017全国卷Ⅲ高考压轴卷
文科数学
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
A
A
D
A
B
D
C
A
C
考点分析及详解
1.B 解析:;,=.
2.D考察复数的运算及实部虚部意义
3.B简单古典概型的考察,共十个事件,3个满足题意
4.A.命题关系题充要条件
5.A因为,由等差数列前项和公式得,
6.D棱柱与圆柱的组合体。
7.A三角函数的简单性质,本题可用直接法或排除法。
8.由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知:数学成绩大于等于90的人数为10,因此输出结果为10. 故选B.
9.由是棱的中点,易证∥,
∥面,由线面平行性质定理,过且过的平面与
面的交线平行于,即为. 由正方体的边长为,
截面是以为腰,为上底,为下底的等腰梯形,故周长为,故选A.
10.因为当时,函数有,
所以函数在上单调递增,在上单调递减,当时函
数有极大值为根据奇函数的对称性,作出其函数图像如图所示:
由函数图像可知和有两个不同交点,故答案选C.
11.本题可利用同构,来构造函数。
12.知,过I、III象限的渐近线的倾斜角为,则,,因此△的面积可以表示为,解得,则. 故选C.
13.|a+2b|==.故选B.
14.提醒:考虑首项符不符合
15.提示利用圆心在直线上求出m的值为-4,再利用勾股定理。
16.①②③④⑤
试题分析:①对任意,关于的不等式恒成立, 即,恒成立,令,,只需即;②若存在,使得不等式成立,由①可知只需,即;③若对任意及任意,不等式恒成立,即,即,所以;④若对任意,存在,使得不等式成立,则,即,所以;⑤若存在及,使得不等式成立,则,即,所以.
17.(1).………………6分
(2)又因为,则为的重心,以、为邻边作平行四边形,因为,
所以,在中,,.
由正弦定理可得,解得且.
因此
18).解:(Ⅰ)近10个月养鱼场的月平均利润为
(千万元)近10个月远洋捕捞队的月平均利润为(千万元).
(Ⅱ)依题意得满足的条件为
设两个项目的利润之和为,则,
如图所示,作直线,平移直线知其过点A时,取最大值,
由得所以A的坐标为,
此时的最大值为(千万元),
所以公司投资养鱼场4千万元,远洋捕捞队2千万元时,两个项目的月平均利润之和最大.
19.(1)证明:∵四边形是菱形,∴
∵平面∴
∴平面
∴平面⊥平面
(2)设与的交点为,,
由(1)得平面,
∵平面∴,
∵,∴,
∴,∴
∴,
∵,∴
∴,∴,∴
∴.
20.焦点坐标为 可知
所以所以抛物线的方程为
(Ⅱ)当直线垂直于轴时,与相似,
所以
当直线与轴不垂直时,设直线AB方程为
设,,,,
解 整理得 ,所以
综上
21解:(Ⅰ),.
∵且,∴∴函数的单调递增区间为.
(Ⅱ)∵,∴,
∴切线的方程为, 即, ①
设直线与曲线相切于点,
∵,∴,∴,∴.
∴直线也为,即,②
由①②得,∴.
下证:在区间(1,+)上存在且唯一.
由(Ⅰ)可知,在区间上递增.
又,,
结合零点存在性定理,说明方程必在区间上有唯一的根,这个根就是所求的唯一,所以有且仅有一个.
22.解(1)∵,∴,
由得曲线的极坐标方程为,
∵,∴曲线的极坐标方程为;
(2)由(1)得,,
∴
∵,∴,∴,
∴的取值范围为.
23.解:(1)∵,∴,
∴,
∴,∴,∴实数的最大值为1;
(2)当时,
∴,
∴或
∴,∴实数的取值范围是.