- 974.50 KB
- 2021-06-23 发布
铁人中学2017级高二学年下学期开学考试
数学(文)试题
试题说明:1、本试题满分150分,答题时间120分钟
2、请将答案填写在答题卡上,考试结束后只交答题卡
第Ⅰ卷 选择题部分
一、选择题(每小题只有一个选项正确,每小题分,共分)
1.已知条件p:,条件q:,则是的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2. 命题“存在实数,”的否定为( )
A.存在实数, B.对所有的实数,
C.不存在实数, D.对所有的实数,
3.从个红球、个白球中随机取出个球,则取出的个球不全是红球的概率是( )
A. B. C. D.
4.阅读下面的程序框图,运行相应的程序,则输出i的值为( )
A. B.
C. D.
5. 用秦九韶算法计算多项式,当时,的值为( )
A. B. C. D.
6.已知一个进制的数与十进制的数相等,那么=( )
A.或 B. C. D.都不对
7.设双曲线()的半焦距为,直线过,两点,已知原点到直线的距离为,则双曲线的离心率为( )
A. B. C. D.
8.在棱长为的正方体中,点为底面的中心,在正方体内随机取一点,则点到点的距离大于的概率为( )
A. B. C. D.
9.现有名工人某天生产同一零件,生产的件数是,,,,,,,,,,设其平均数为,中位数为,众数为,则有( )
A. B. C. D.
10.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为的正方形将其包含在内,并向该正方形内随机投掷个点,已知恰有个点落在阴影部分,据此可估计阴影部分的面积是( )
A. B. C. D.
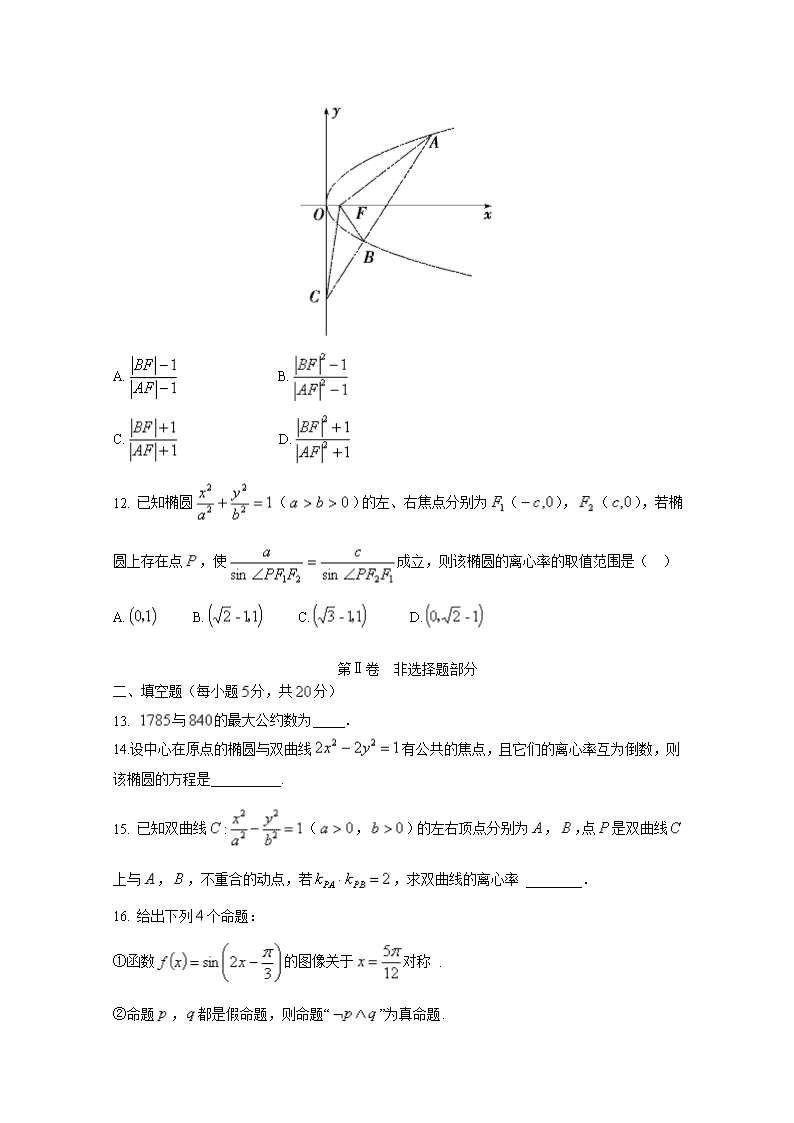
11.如图,设抛物线的焦点为,不经过焦点的直线上有三个不同的点,,,其中点,在抛物线上,点在轴上,则与的面积之比是( )
A. B.
C. D.
12. 已知椭圆()的左、右焦点分别为(),(),若椭圆上存在点,使成立,则该椭圆的离心率的取值范围是( )
A. B. C. D.
第Ⅱ卷 非选择题部分
二、 填空题(每小题分,共分)
13. 与的最大公约数为 .
14.设中心在原点的椭圆与双曲线有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是__________.
15. 已知双曲线:(,)的左右顶点分别为,,点是双曲线上与,,不重合的动点,若,求双曲线的离心率 ________.
16. 给出下列个命题:
①函数的图像关于对称 .
②命题,都是假命题,则命题“”为真命题.
③在空间中,,是两条不重合的直线,,是两个不重合的平面,如果,
,,那么.
④将函数的图象向右平移个单位,得到函数的图象.
其中正确命题的序号是________.
三、解答题(共小题,共70分)
17. (本小题满分10分)设甲、乙、丙三个乒乓球协会的运动员人数分别为27、9、18.现采用分层抽样的方法从这三个协会中抽取6名运动员组队参加比赛.
(1)求应从这三个协会中分别抽取的运动员的人数;
(2)将抽取的6名运动员进行编号,编号分别为、、、、、.现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设为事件“编号为和的两名运动员中至少有人被抽到”,求事件发生的概率.
18. (本小题满分分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准 (吨),一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年位居民每人的月均用水量(单位:吨),将数据按照,,,分成组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有万居民,估计全市居民中月均用水量不低于吨的人数,并说明理由;
(3)若该市政府希望使%的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
19. (本小题满分分)如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(此数学题满分为分)的得分情况.乙组某个数据的个位数模糊,记为,已知甲、乙两组的平均成绩相同.
(1)求的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,
求这两名同学的得分之和低于分的概率.
20. (本小题满分分)已知直线交抛物线于,两点,且的中点的横坐标为.求弦的长.
21. (本小题满分分)假设关于某设备的使用年限 (年)和所支出的年平均维修费用 (万元)(即维修费用之和除以使用年限),有如下的统计资料:
(1)求回归方程.
(2)估计使用年限为年时所支出的年平均维修费用是多少?
参考公式:
;.
22. (本小题满分分)已知中心在原点,焦点在轴上的椭圆,离心率,是经过抛物线的焦点.
(1)求椭圆的标准方程;
(2)如图,若过点的直线(斜率不等于零)与椭圆交于不同的两点,(在,之间),试求与面积之比的取值范围.
铁人中学2017级高二学年下学期开学考试
数学(文)试题(答案)
第Ⅰ卷 选择题、填空题部分
一、选择题(每小题只有一个选项正确,每小题分,共分)
1
2
3
4
5
6
7
8
9
10
11
12
B
D
C
B
C
C
A
B
D
C
A
B
二、 填空题(每小题分,共分)
13、 . 14、 .
15、 . 16、 ①④________.
1.答案:B
2. 答案:D
解析:命题“存在实数,”为特称命题,其否定为全称命题,注意否定量词的同时否定结论.故选D.
3.答案:C
4. 答案:B
5. 答案:C
6. 答案:C
解析:,所以,即,解得或(舍去).
7. 答案:A
解析:的方程为,原点到直线的距离,
整理得,所以或.所以或.
因为,所以(舍去).故,故选A.
8. 答案:B
9. 答案:D
解析:总和为,;样本数据分布最广,即频率最大,为众数,;中位数为.
10. 答案:C
11. 答案: A
解析:由图形可知,与有公共的顶点,且,,,三点共线,易知与的面积之比就等于.由抛物线方程知焦点,作准线,则的方程为
.因为点,在抛物线上,过,分别作,与准线垂直,垂足分别为点,,且与轴分别交于点,.由抛物线定义,得,
.在中,,所以.
12. 答案:B
解析:由正弦定理及,得.
在中,设,则,则,即,
得.又,所以.
由,得,显然恒成立;
由,得,即,解得或(舍去).又,所以的取值范围是,故选B.
13.答案:
14.答案:
解析:设椭圆方程为,焦点为,.双曲线的焦点为,,,所以椭圆的离心率为,据题意得,所以,而,所以.椭圆方程为.
15.答案:
16.答案:①④
第Ⅱ卷 解答题部分
17. (本小题满分分)
答案:(1)甲、乙、丙三个乒乓球协会的运动员人数分别为、、,则共有人,分层抽样的方法从这三个协会中抽取名运动员,则抽样比为,则人、人、人,
所以应从甲、乙、丙三个协会中抽取的运动员人数分别为3、1、2.
(2)①从6名运动员中随机抽取2人参加双打比赛的所有可能结果为{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共15种.
②编号为A5和A6的两名运动员中至少有1人被抽到的所有可能结果为{A1,A5},{A1,A6},{A2,A5},{A2,A6},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共9种.
因此,事件A发生的概率P(A)==.
18. (本小题满分分)
答案:(1)由频率分布直方图知,月均用水量在[0,0.5)中的频率为0.08×0.5=0.04,
同理,在[0.5,1),[1.5,2),[2,2.5),[2,5.3),[3,3.5),[3.5,4),[4,4.5]中的频率分别为0.08,0.20,0.26,0.06,0.04,0.02.由0.04+0.08+0.5×+0.20+0.26+0.5×+0.06+0.04+0.02=1,
解得=0. 30.
(2)由(1)可知,位居民每人月均用水量不低于吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率,可以估计全市30万居民中月均用水量不低于3吨的人数为
300 000×0.12=36 000.
(3)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85,
而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,
所以.
由,解得.
所以,估计月用水量标准为吨时,%的居民每月的用水量不超过标准.
19. 答案:(1),,所以,
又,
,
所以,所以甲组成绩比乙组稳定.
(2)记甲组名同学为:,,,;乙组名同学为:,,,.分别从甲、乙两组中各抽取一名同学所有可能的结果为:(,),(,),(,),(,),(,),(,),(,),(,),(,),(,),(,
),(,),(,),(,),(,),(,),共种,其中得分之和低于分的共种,所以得分之和低于分的概率.
20.答案:设,两点的坐标分别为,,的中点的坐标为.
将代入中,得方程,
当,即且时,方程有两实根,.
根据韦达定理知.又,故,解得或(舍)
从而.
21. 答案:(1)从散点图可以看出,这些点大致分布在一条直线的附近,因此,两变量呈线性相关关系.
,;
,,,,
所以,
可求回归方程是
(2)由(1)知,当时, (万元).
故估计使用年限为年时所支出的年平均维修费用是万元.
22. 答案:(1)设椭圆方程为(),则①
因为抛物线的焦点为,所以 ②
由①②解得,.所以椭圆的标准方程为.
(2)如下图所示,由题意知直线的斜率存在且不为零,
设的方程为
()③
将③代入,整理得.
由得.设,,则 ④
令,则.
由此得,,且.由④得,
,
所以,即.因为,所以
解得.又因为,所以.
所以和面积之比的取值范围是(,).