专题30 空间点、线、面的位置关系-2018年高考数学（理）热点题型和提分秘籍 35页

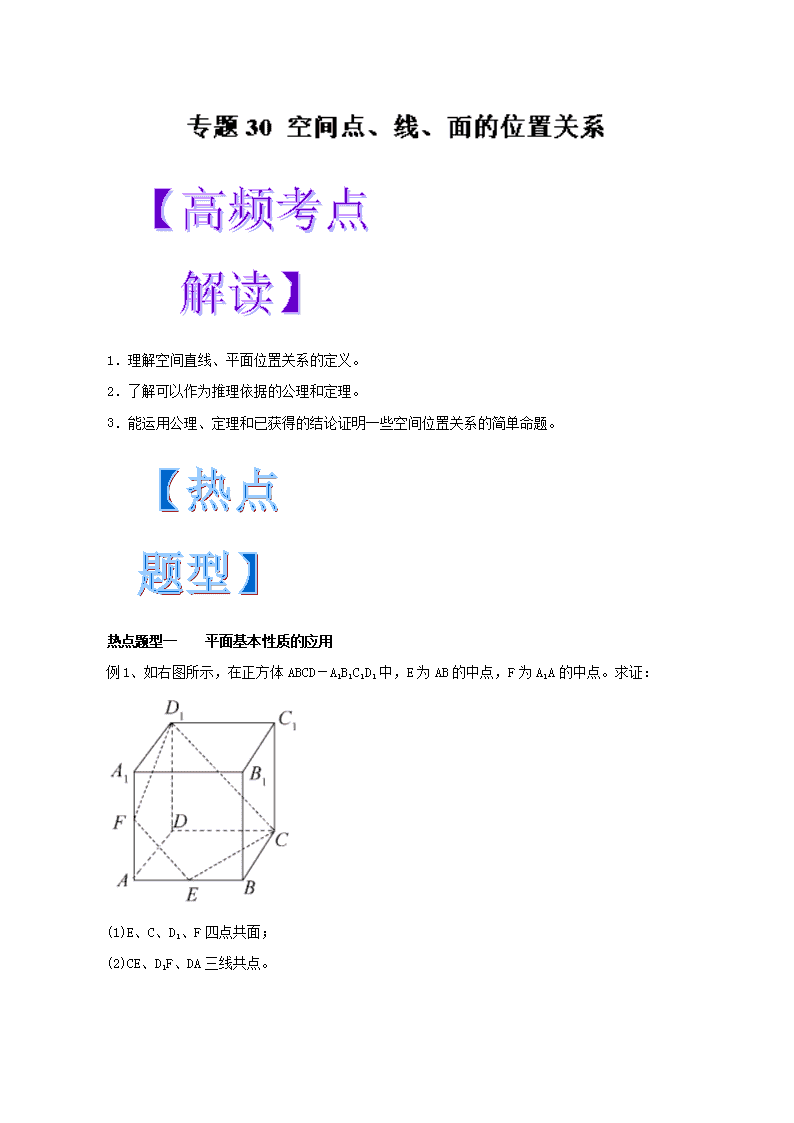
‎【高频考点解读】‎ ‎1．理解空间直线、平面位置关系的定义。‎ ‎2．了解可以作为推理依据的公理和定理。‎ ‎3．能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题。‎ ‎【热点题型】‎ 热点题型一 平面基本性质的应用 例1、如右图所示，在正方体ABCD－A1B1C1D1中，E为AB的中点，F为A1A的中点。求证：‎ ‎ ‎ ‎(1)E、C、D1、F四点共面；‎ ‎(2)CE、D1F、DA三线共点。‎ 又A1D1綊B1C1綊BC，‎ ‎∴四边形A1D1CB为平行四边形。‎ ‎∴A1B∥CD1，从而EF∥CD1。‎ ‎∴EF与CD1确定一个平面。‎ ‎∴E、F、D1、C四点共面。‎ ‎【提分秘籍】‎ 证明点共面或线共面的常用方法 ‎(1)直接法：证明直线平行或相交，从而证明线共面。‎ ‎(2)同一法：先确定一个平面，再证明有关点、线在此平面内。‎ ‎(3)辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合。‎ ‎【举一反三】 ‎ 已知在空间四边形ABCD中，E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且＝＝(如图所示)，求证：三条直线EF、GH、AC交于一点。‎ 热点题型二 异面直线的判定 例2、如图所示，正方体ABCD－A1B1C1D1中，M、N分别是A1B1、B1C1的中点。问：‎ ‎(1)AM和CN是否是异面直线？说明理由。‎ ‎(2)D1B和CC1是否是异面直线？说明理由。‎ 解析：(1)不是异面直线。理由：‎ 连接MN、A1C1、AC。‎ ‎∵M、N分别是A1B1、B1C1的中点，∴MN∥A1C1。‎ 又∵A1A綊C1C，‎ ‎∴A1ACC1为平行四边形。‎ ‎∴A1C1∥AC，得到MN∥AC。‎ ‎∴A、M、N、C在同一平面内，‎ 故AM和CN不是异面直线。‎ ‎【提分秘籍】 ‎ 异面直线的判定方法 ‎(1)反证法：先假设两条直线不是异面直线，即两条直线平行或相交，由假设出发，经过严格的推理，导出矛盾，从而否定假设，肯定两条直线异面。此法在异面直线的判定中经常用到。‎ ‎(2)判定定理法：平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线。‎ ‎【举一反三】 ‎ 如图，正方体ABCD－A1B1C1D1中，M、N分别为棱C1D1、C1C的中点，有以下四个结论：‎ ‎①直线AM与CC1是相交直线；‎ ‎②直线AM与BN是平行直线；‎ ‎③直线BN与MB1是异面直线；‎ ‎④直线AM与DD1是异面直线。‎ 其中正确的结论为__________(注：把你认为正确的结论的序号都填上)‎ 热点题型三 异面直线所成的角 ‎ 例3．如图所示，A是△BCD所在平面外一点，AD＝BC，E、F分别是AB、CD的中点。‎ ‎ ‎ ‎(1)若EF＝AD，求异面直线AD与BC所成的角；‎ ‎(2)若EF＝AD，求异面直线AD与BC所成的角。‎ 解析：设G是AC的中点，连结EG、FG。如图所示。‎ ‎∵E、F分别是AB、CD的中点，‎ ‎∴EG∥BC且EG＝BC，FG∥AD且FG＝AD。‎ ‎∵AD＝BC，‎ ‎∴EG＝FG＝AD，‎ ‎∴EG与FG所成的锐角(或直角)为AD与BC所成的角。‎ ‎【提分秘籍】‎ ‎1．求异面直线所成角的常用方法及类型 常用方法是平移法，平移的方法一般有三种类型：利用图中已有的平行线平移；利用特殊点(线段的端点或中点空间某特殊点)作平行线平移；补形平移。‎ ‎2．求异面直线所成角的三个步骤 ‎(1)作：通过作平行线，得到相交直线。‎ ‎(2)证：证明相交直线夹角为异面直线所成的角。‎ ‎(3)求：通过解三角形，求出该角。‎ ‎【举一反三】 ‎ 在正方体ABCD－A1B1C1D1中，M，N分别为A1B1，BB1的中点，则异面直线AM与CN所成角的余弦值为(　　)‎ A.　　　B. C.　　　D. 解析：如图，取AB的中点E，连接B1E，‎ ‎【高考风向标】‎ ‎ ‎ ‎1.【2017课标1，理16】如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为_______.‎ ‎【答案】 ‎2.【2017课标1，理18】如图，在四棱锥P-ABCD中，AB//CD，且.‎ ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC，，求二面角A-PB-C的余弦值.‎ ‎【答案】（1）见解析；（2）.‎ ‎（2）在平面内做，垂足为，‎ 由（1）可知， 平面，故，可得平面.‎ 以为坐标原点， 的方向为轴正方向， 为单位长，建立如图所示的空间直角坐标系.‎ 设是平面的法向量，则 ，即，‎ 可取.‎ 则，‎ 所以二面角的余弦值为.‎ ‎1.【2016高考新课标1卷】平面过正方体ABCD-A1B‎1C1D1的顶点A,//平面CB1D1,平面ABCD=m,平面AB B‎1A1=n,则m、n所成角的正弦值为 ‎(A) (B) (C) (D)‎ ‎【答案】A ‎2.【2016高考新课标1卷】（本小题满分为12分）如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD, ,且二面角D-AF-E与二面角C-BE-F都是．‎ ‎（I）证明：平面ABEF平面EFDC；‎ ‎（II）求二面角E-BC-A的余弦值．‎ ‎【答案】（I）见解析（II）‎ ‎【解析】‎ ‎（Ⅰ）由已知可得，，所以平面．‎ 又平面，故平面平面．‎ 设是平面的法向量，则 ‎，即，‎ 所以可取．‎ 设是平面的法向量，则，‎ 同理可取．则．‎ 故二面角EBCA的余弦值为．‎ ‎3.【2016高考新课标2理数】如图，菱形的对角线与交于点，，点 分别在上，，交于点．将沿折到位置，．‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）求二面角的正弦值．‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ ‎（Ⅱ）如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系，则，，，，，，，. ‎ ‎1.【2015高考四川，理18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设的中点为，的中点为 ‎（1）请将字母标记在正方体相应的顶点处（不需说明理由）‎ ‎（2）证明：直线平面 ‎（3）求二面角的余弦值.‎ ‎【答案】（1）点F、G、H的位置如图所示.‎ ‎（2）详见解析.（3）‎ ‎【解析】（1）点F、G、H的位置如图所示.‎ ‎（2）连结BD，设O为BD的中点.‎ ‎（3）连结AC，过M作于P. ‎ ‎（另外，也可利用空间坐标系求解）‎ ‎2.【2015高考湖北，理19】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马中，侧棱底面，且，过棱的中点，作交于点，连接 ‎ ‎（Ⅰ）证明：．试判断四面体是否为鳖臑，若是，写出其每个面的直角（只需写 出结论）；若不是，说明理由；‎ ‎（Ⅱ）若面与面所成二面角的大小为，求的值．‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ ‎ ‎ ‎（Ⅱ）如图1，在面内，延长与交于点，则是平面与平面 ‎ 的交线．由（Ⅰ）知，，所以．‎ 故是面与面所成二面角的平面角， ‎ 设，，有，‎ 在Rt△PDB中, 由, 得, ‎ 则 , 解得. ‎ 所以 ‎ 故当面与面所成二面角的大小为时，. ‎ ‎（解法2）‎ ‎（Ⅰ）如图2，以为原点，射线分别为轴的正半轴，建立空间直角坐标系.‎ ‎ 设，，则，，点是的中 点，‎ 所以，，‎ 于是，即. ‎ 又已知，而，所以. ‎ 因, , 则, 所以.‎ 由平面，平面，可知四面体的四个面都是直角三角形，‎ 即四面体是一个鳖臑，其四个面的直角分别为. ‎ ‎3.【2015高考广东，理18】如图2，三角形所在的平面与长方形所在的平面垂直，，，.点是边的中点，点、分别在线段、上，且，．‎ ‎（1）证明：；‎ ‎（2）求二面角的正切值；‎ ‎（3）求直线与直线所成角的余弦值．‎ 图2‎ P A B C D E F G ‎【答案】（1）见解析；（2）；（3）．‎ ‎【解析】（1）证明：∵ 且点为的中点，‎ ‎∴ ，又平面平面，且平面平面，平面，‎ ‎∴ 平面，又平面，‎ ‎∴ ；‎ P A B C D E F G ‎（3）如下图所示，连接，‎ ‎∵ ，即，‎ ‎∴ ，‎ ‎∴ 为直线与直线所成角或其补角，‎ 在中，，，‎ P A B C D E F G 由余弦定理可得，‎ ‎∴ 直线与直线所成角的余弦值为．‎ ‎1．（2014·辽宁卷）已知m，n表示两条不同直线，α表示平面．下列说法正确的是(　　)‎ A．若m∥α，n∥α，则m∥n ‎ B．若m⊥α，n⊂α，则m⊥n C．若m⊥α，m⊥n，则n∥α ‎ D．若m∥α，m⊥n，则n⊥α ‎2．（2014·福建卷）在平面四边形ABCD中，AB＝BD＝CD＝1，AB⊥BD，CD⊥BD.将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图15所示．‎ ‎(1)求证：AB⊥CD；‎ ‎(2)若M为AD中点，求直线AD与平面MBC所成角的正弦值．‎ 图15‎ ‎【解析】解：(1)证明：∵平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，AB⊂平面ABD，AB⊥BD，∴AB⊥平面BCD.‎ 又CD⊂平面BCD，∴AB⊥CD.‎ ‎(2)过点B在平面BCD内作BE⊥BD.‎ 由(1)知AB⊥平面BCD，BE⊂平面BCD，BD⊂平面BCD，∴AB⊥BE，AB⊥BD.‎ 以B为坐标原点，分别以，，的方向为x轴，y轴，z轴的正方向建立空间直角坐标系(如图所示)．‎ ‎3．（2014·新课标全国卷Ⅱ）直三棱柱ABCA1B‎1C1中，∠BCA＝90°，M，N分别是A1B1，A‎1C1的中点，BC＝CA＝CC1，则BM与AN所成角的余弦值为(　　)‎ A. B. C. D. ‎【答案】C　【解析】如图，E为BC的中点．由于M，N分别是A1B1，A‎1C1的中点，故MN∥B‎1C1且MN＝B‎1C1，故MN綊BE，所以四边形MNEB为平行四边形，所以EN綊BM，所以直线AN，NE所成的 ‎4．（2014·四川卷）三棱锥A BCD及其侧视图、俯视图如图14所示．设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP.‎ ‎(1)证明：P是线段BC的中点；‎ ‎(2)求二面角A NP M的余弦值．‎ ‎　‎ 图14‎ ‎【解析】解：(1)如图所示，取BD的中点O，连接AO，CO.‎ 由侧视图及俯视图知，△ABD，△BCD为正三角形，‎ 所以AO⊥BD，OC⊥BD.‎ 因为AO，OC⊂平面AOC，且AO∩OC＝O，‎ 所以BD⊥平面AOC.‎ 又因为AC⊂平面AOC，所以BD⊥AC.‎ 取BO的中点H，连接NH，PH.‎ ‎(2)方法一：如图所示，作NQ⊥AC于Q，连接MQ.‎ 由(1)知，NP∥AC，所以NQ⊥NP.‎ 因为MN⊥NP，所以∠MNQ为二面角A NP M的一个平面角．‎ 由(1)知，△ABD，△BCD为边长为2的正三角形，所以AO＝OC＝.‎ 由俯视图可知，AO⊥平面BCD.‎ 因为OC⊂平面BCD，所以AO⊥OC，因此在等腰直角△AOC中，AC＝.‎ 作BR⊥AC于R 因为在△ABC中，AB＝BC，所以R为AC的中点，‎ 所以BR＝＝.‎ 因为在平面ABC内，NQ⊥AC，BR⊥AC，‎ 所以NQ∥BR.‎ 又因为N为AB的中点，所以Q为AR的中点，‎ 所以NQ＝＝.‎ 同理，可得MQ＝.‎ 故△MNQ为等腰三角形，‎ 所以在等腰△MNQ中，‎ cos∠MNQ＝＝＝.‎ 所以M，N，P，于是AB＝(1，0，－)，BC＝(－1，，0)，MN＝(1，0，0)，NP＝.‎ 设平面ABC的一个法向量n1＝(x1，y1，z1)，‎ 由得即 从而 取z1＝1，则x1＝，y1＝1，所以n1＝(，1，1)．‎ 设平面MNP的一个法向量n2＝(x2，y2，z2)，由，‎ 得 即 从而 取z2＝1，则y2＝1，x2＝0，所以n2＝(0，1，1)．‎ 设二面角A NP M的大小为θ，则cos θ＝＝＝.‎ 故二面角ANPM的余弦值是.‎ ‎【高考冲刺】‎ ‎ 1．给出下列说法：①梯形的四个顶点共面；②三条平行直线共面；③有三个公共点的两个平面重合；④三条直线两两相交，可以确定3个平面。其中正确的序号是(　　)‎ A．① B．①④‎ C．②③ D．③④‎ 答案：A ‎2．如图所示的是正方体或四面体，P，Q，R，S分别是所在棱的中点，这四个点不共面的是(　　)‎ A B C D 解析：A中PS∥QR，故共面；B中PS与QR相交，故共面；C中四边形PQRS是平行四边形，所以共面，故选D。‎ 答案：D ‎3．已知空间中有三条线段AB，BC和CD，且∠ABC＝∠BCD，那么直线AB与CD的位置关系是(　　)‎ A．AB∥CD B．AB与CD异面 C．AB与CD相交 D．AB∥CD或AB与CD异面或AB与CD相交 解析：若三条线段共面，如果AB，BC，CD构成等腰三角形，则直线AB与CD相交，否则直线AB与CD平行；若不共面，则直线AB与CD是异面直线，故选D。‎ 答案：D ‎4．如图，α∩β＝l，A、B∈α，C∈β，且C∉l，直线AB∩l＝M，过A，B，C三点的平面记作γ，则γ与β的交线必通过(　　)‎ A．点A B．点B C．点C但不过点M D．点C和点M 答案：D ‎5．已知α、β为平面，A、B、M、N为点，a为直线，下列推理错误的是(　　)‎ A．A∈a，A∈β，B∈a，B∈β⇒a⊂β B．M∈α，M∈β，N∈α，N∈β⇒α∩β＝MN C．A∈α，A∈β⇒α∩β＝A D．A、B、M∈α，A、B、M∈β，且A、B、M不共线⇒α、β重合 解析：∵A∈α，A∈β，∴A∈α∩β。‎ 由公理可知α∩β为经过A的一条直线而不是A。故α∩β＝A的写法错误。‎ 答案：C ‎6．如图，正四棱柱ABCD—A1B1C1D1(底面为正方形，侧棱与底面垂直)中，AA1＝2AB，则异面直线A1B与AD1所成角的余弦值为(　　)‎ A. B. C. D. 解析：连接BC1，A1C1，则A1B与BC1所成角即为所求。‎ 在△A1BC1中，‎ 设AB＝a，‎ 则A1B＝BC1＝a，A1C1＝a，‎ ‎∴cos∠A1BC1‎ ‎＝＝。‎ 答案：D ‎7．设a，b，c是空间的三条直线，下面给出四个命题：‎ ‎①设a⊥b，b⊥c，则a∥c；‎ ‎②若a，b是异面直线，b，c是异面直线，则a，c也是异面直线；‎ ‎③若a和b相交，b和c相交，则a和c也相交；‎ ‎④若a和b共面，b和c共面，则a和c也共面。‎ 其中真命题的个数是________。‎ 答案：0‎ ‎8．若两条异面直线所成的角为60°，则称这对异面直线为“黄金异面直线对”，在连接正方体各顶点的所有直线中，“黄金异面直线对”共有________对。‎ 解析：正方体如图，若要出现所成角为60°的异面直线，则直线需为面对角线，以AC为例，与之构成黄金异面直线对的直线有4条，分别是A′B，BC′，A′D，C′D，正方体的面对角线有12条，所以所求的黄金异面直线对共有＝24对(每一对被计算两次，所以记好要除以2)。‎ 答案：24‎ ‎9．如图，已知圆柱的轴截面ABB1A1是正方形，C是圆柱下底面弧AB的中点，C1是圆柱上底面弧A1B1的中点，那么异面直线AC1与BC所成角的正切值为________。‎ 解析：取圆柱下底面弧AB的另一中点D，连接C1D，AD，‎ 答案： ‎10．在四棱锥P－ABCD中，底面是边长为2的菱形，∠DAB＝60°，对角线AC与BD交于点O，PO⊥平面ABCD，PB与平面ABCD所成角为60°。‎ ‎(1)求四棱锥的体积。‎ ‎(2)若E是PB的中点，求异面直线DE与PA所成角的余弦值。‎ 解析：(1)在四棱锥P－ABCD中，‎ 因为PO⊥平面ABCD，‎ 所以∠PBO是PB与平面ABCD所成的角，即∠PBO＝60°。‎ 在Rt△POB中，因为BO＝AB·sin30°＝1，‎ 又PO⊥OB，所以PO＝BO·tan60°＝，‎ 因为底面菱形的面积S菱形ABCD＝2。‎ 所以四棱锥P－ABCD的体积 VP－ABCD＝×2×＝2。‎ 因为四边形ABCD为菱形，且∠DAB＝60°，‎ 所以△ABD为正三角形。‎ 又因为∠PBO＝60°，BO＝1，‎ 所以PB＝2，所以PB＝PD＝BD，即△PBD为正三角形，‎ 所以DF＝DE＝，‎ 所以cos∠DEF＝ ‎＝＝＝。‎ 即异面直线DE与PA所成角的余弦值为。‎ ‎11．如图所示，已知二面角α－MN－β的大小为60°，菱形ABCD在平面β内，A，B两点在棱MN上，∠BAD＝60°，E是AB的中点，DO⊥面α，垂足为O。‎ ‎(1)证明：AB⊥平面ODE；‎ ‎(2)求异面直线BC与OD所成角的余弦值。‎ 解析：(1)如图，因为DO⊥α，AB⊂α，所以DO⊥AB。‎ 连接BD，由题设知，△ABD是正三角形，又E是AB的中点，所以DE⊥AB。‎ 又DO∩DE＝D，故AB⊥平面ODE。‎ 故异面直线BC与OD所成角的余弦值为。‎ ‎12．如图所示，在三棱锥P－ABC中，PA⊥平面ABC，∠BAC＝60°，PA＝AB＝AC＝2，E是PC的中点。‎ ‎(1)求证：AE与PB是异面直线；‎ ‎(2)求异面直线AE和PB所成角的余弦值；‎ ‎(3)求三棱锥A－EBC的体积。‎ 解析：(1)假设AE与PB共面，设平面为α。‎ 因为A∈α，B∈α，E∈α，‎ 所以平面α即为平面ABE，所以P∈平面ABE，‎ 这与P∉平面ABE矛盾，‎ 所以AE与PB是异面直线。‎ ‎(3)因为E是PC的中点，所以点E到平面ABC的距离为PA＝1，‎ VA－EBC＝VE－ABC＝××1＝。‎ ‎ ‎