人教版九年级（上）数学二次函数专练 4页

‎1、二次函数y=（x+3）2+7的顶点坐标是（　　）‎ A．（﹣3，7） B．（3，7） C．（﹣3，﹣7） D．（3，﹣7）‎ ‎2、若函数y=2x2﹣8x+m的图象上有两点A（x1，y1），B（x2，y2），若x1＜x2＜﹣2，则（　　）‎ A．y1＜y2 B．y1＞y2‎ C．y1=y2 D．y1、y2、的大小不确定 ‎3、若关于x的一元二次方程有两个不相等的实数根，那么k的取值范围是 A．k≠0  B．k＞4  C． k＜4 D． k＜4且k≠0‎ ‎4、若点，，都在抛物线 上，则下列结论正确的是（ ）‎ A. B. ‎ C. D. ‎ ‎5、下列关于函数的图象说法：①图象是一条抛物线；②开口向下；③对称轴是y轴；④顶点（0，0），其中正确的有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎6、二次函数图象上部分点的坐标对应值列表如下：‎ x ‎…‎ ‎﹣3‎ ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎…‎ y ‎…‎ ‎﹣3‎ ‎﹣2‎ ‎﹣3‎ ‎﹣6‎ ‎﹣11‎ ‎…‎ 则该函数图象的对称轴是（　　）‎ A．x＝﹣3 B．x＝﹣2 C．x＝﹣1 D．x＝0‎ ‎7、把抛物线y＝2x2先向左平移3个单位，再向上平移4个单位，所得抛物线的函数表达式为（　　）‎ A．y＝2（x+3）2+4 B．y＝2（x+3）2﹣4 ‎ C．y＝2（x﹣3）2﹣4 D．y＝2（x﹣3）2+4‎ ‎8、一元二次方程x2+4x＝5配方后可变形为（　　）‎ A．（x+2）2＝5 B．（x+2）2＝9 C．（x﹣2）2＝9 D．（x﹣2）2＝21‎ ‎9、一元二次方程x2+x+1＝0的根的情况是（　　）‎ A．有两个不相等的实数根 B．有两个相等的实数根 ‎ C．无实数根 D．无法确定 ‎10、某厂一月份生产产品50台，计划二、三月份共生产产品120台，设二、三月份平均每月增长率为x，根据题意，可列出方程为（　　）‎ A．50（1+x）2＝60 ‎ B．50（1+x）2＝120 ‎ C．50+50（1+x）+50（1+x）2＝120 ‎ D．50（1+x）+50（1+x）2＝120‎ ‎11、对于抛物线y＝（x﹣1）2+2的说法错误的是（　　）‎ A．抛物线的开口向上 ‎ B．抛物线的顶点坐标是（1，2） ‎ C．抛物线与x轴无交点 ‎ D．当x＜1时，y随x的增大而增大 4‎ ‎1、抛物线y=﹣x2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是　　．‎ ‎2、已知二次函数的图象与x轴只有一个交点．请写出一组满足条件的a，b的值：a =______，b =________.‎ ‎3、某地区2017年投入教育经费2 500万元，2019年计划投入教育经费3 025万元．则2017年至2019年，该地区投入教育经费的年平均增长率为 ．‎ ‎4、将函数y=﹣2x2的图象沿着x轴向右平移3个单位后所得到的图象的函数表达式为　 　．‎ ‎5、已知二次函数y＝﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m＝0的解为　 　．‎ 6、 若关于x的方程x2+3x+k＝0的一个根是1，则k的值为　 　．‎ ‎7、关于x的方程（a﹣5）x2﹣4x﹣1＝0有实数根，则a满足　 　．‎ ‎8、抛物线y=ax2+bx+c经过点A（4，0），对称轴是直线x=1，则4a-2b+c=　 　．‎ ‎9、（1）解方程：； （2）解不等式组： ‎ ‎（3）x2－8x＋6＝0 　 　 　（4）2(x－1)2＝3x－3‎ ‎1、已知：如图，抛物线y=ax2+bx+c与x轴相交于两点A（1，0），B（3，0），与y轴相交于点C（0，3）．‎ ‎（1）求抛物线的函数关系式；‎ ‎（2）若点D（，m）是抛物线y=ax2+bx+c上的一点，请求出m的值，并求出此时△ABD的面积．‎ 4‎ ‎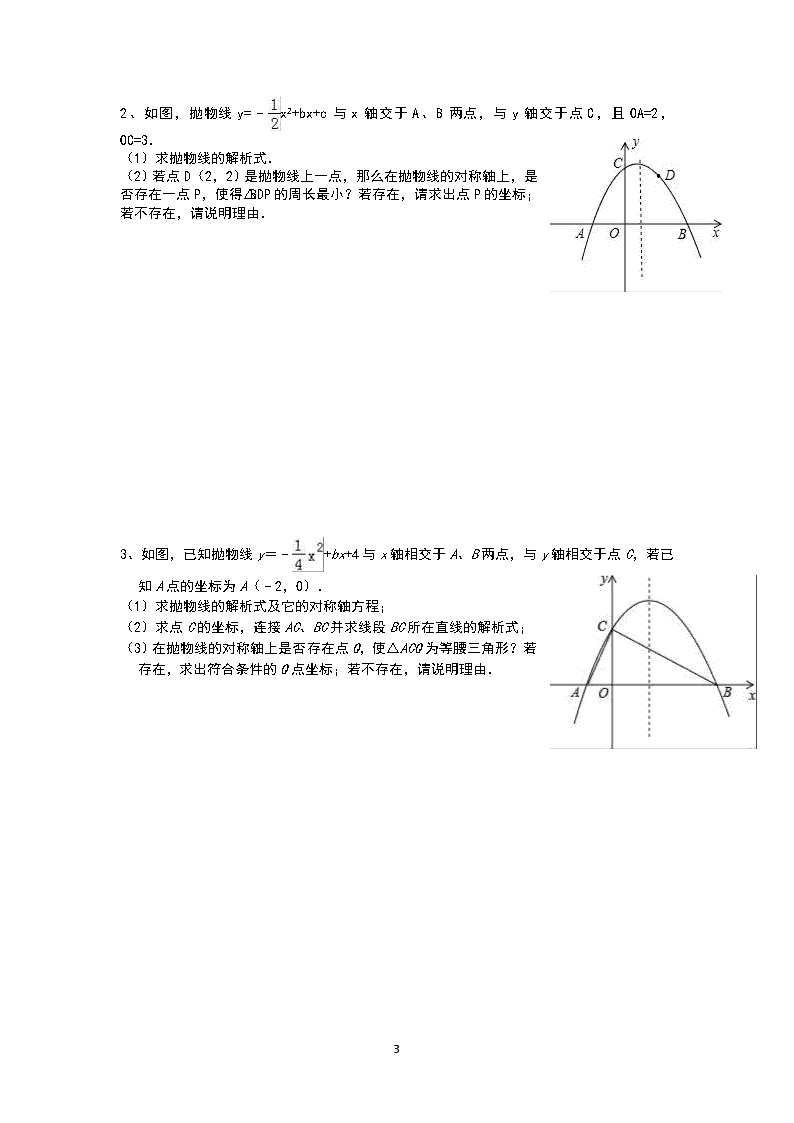2、如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，且OA=2，OC=3．‎ ‎（1）求抛物线的解析式．‎ ‎（2）若点D（2，2）是抛物线上一点，那么在抛物线的对称轴上，是否存在一点P，使得△BDP的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎3、如图，已知抛物线y＝﹣+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．‎ ‎（1）求抛物线的解析式及它的对称轴方程；‎ ‎（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；‎ ‎（3）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．‎ 4‎ ‎4、如图，抛物线y=ax2+bx+c的图象与x轴交于A（﹣1.0），B（3，0）两点，与y轴交于点C（0，﹣3），顶点为D．‎ ‎（1）求此抛物线的解析式．‎ ‎（2）求此抛物线顶点D的坐标和对称轴．‎ ‎（3）探究对称轴上是否存在一点P，使得以点P、D、A为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的P点的坐标，若不存在，请说明理由．‎ ‎5、如图，直线y＝﹣2x+3与x轴交于点C，与y轴交于点B，抛物线y＝ax2+x+c经过B、C两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值？‎ 4‎