2017-2018学年河北省阜城中学高二上第六次月考数学文试题（解析版） 14页

‎2017-2018学年河北省阜城中学高二上第六次月考数学文试题（解析版）‎ 一、选择题：每小题5分,共70分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 抛物线的焦点坐标为（ ）‎ A. B. C. D. ‎ ‎【答案】D 故选：D ‎2. 命题“，使”的否定是（ ）‎ A. ，使 B. 不存在，使 C. ，使 D. ，使 ‎【答案】D ‎【解析】命题“，使”的否定是，使 故选：D ‎3. 命题“若，则”与它的逆命题、否命题、逆否命题中，真命题个数为（ ）‎ A. 0 B. 2 C. 3 D. 4‎ ‎【答案】B ‎【解析】∵c2=0时，结论不成立，∴命题是假命题；‎ 其逆命题是：若ac2＞bc2，则a＞b，是真命题；‎ 根据逆命题与否命题是互为逆否命题，命题与其逆否命题同真同假，‎ 否命题为真，逆否命题为假．‎ 故选B．‎ ‎4. 已知双曲线 的离心率为2，那么双曲线的渐近线方程为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】双曲线 的离心率为2，‎ 可得，即，可得，‎ 双曲线的渐近线方程为：y=±，‎ 即．‎ 故选：C．‎ ‎5. 已知两条直线，，则“”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要 ‎【答案】A ‎【解析】由2（m2﹣1）﹣6=0，解得m=±2，‎ 解得验证：m=±2时，两条直线都平行，因此m=±2．‎ ‎∴“m=2”是“L1∥L2”的充分不必要条件．‎ 故选：A．‎ ‎6. 过抛物线上的点的切线的倾斜角（ ）‎ A. B. C. D. 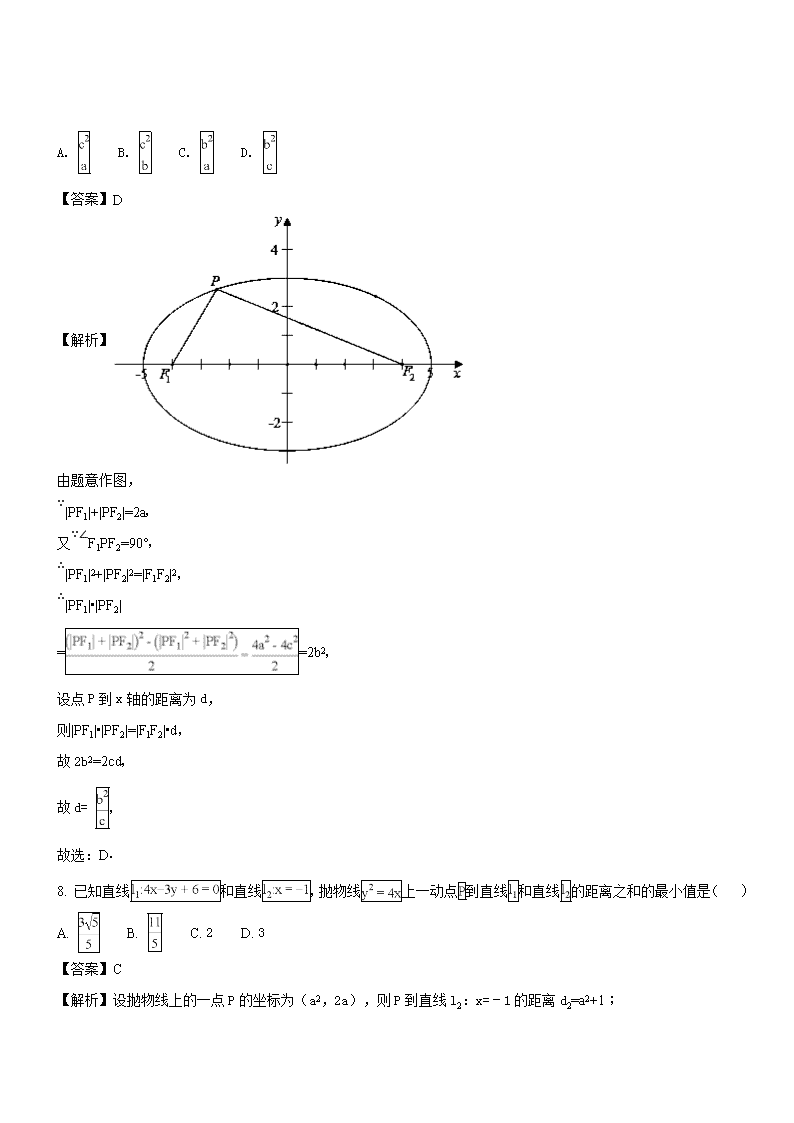‎ ‎【答案】B ‎【解析】y=x2的导数为y′=2x，‎ 在点点的切线的斜率为k=2×=1，‎ 设所求切线的倾斜角为α（0°≤α＜180°），‎ 由k=tanα=1，‎ 解得α=45°．‎ 故选：B．‎ ‎7. 已知椭圆的两个焦点分别为，，若点在椭圆上，且，则点到轴的距离为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 由题意作图，‎ ‎∵|PF1|+|PF2|=2a，‎ 又∵∠F1PF2=90°，‎ ‎∴|PF1|2+|PF2|2=|F1F2|2，‎ ‎∴|PF1|•|PF2|‎ ‎==2b2，‎ 设点P到x轴的距离为d，‎ 则|PF1|•|PF2|=|F1F2|•d，‎ 故2b2=2cd，‎ 故d= ，‎ 故选：D．‎ ‎8. 已知直线和直线，抛物线上一动点到直线和直线的距离之和的最小值是（ ）‎ A. B. C. 2 D. 3‎ ‎【答案】C ‎【解析】设抛物线上的一点P的坐标为（a2，2a），则P到直线l2：x=﹣1的距离d2=a2+1；‎ P到直线l1：4x﹣3y+6=0的距离d1=‎ 则d1+d2=a2+1+=‎ 当a=时，P到直线l1和直线l2的距离之和的最小值为2‎ 故选：C ‎9. 已知函数在上是单调函数，则实数的取值范围是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】f（x）=﹣x3+2ax2﹣x﹣3的导数为f′（x）=﹣3x2+4ax﹣1，‎ ‎∵函数f（x）在（﹣∞，+∞）上是单调函数，‎ ‎∴在（﹣∞，+∞）上f′（x）≤0恒成立，‎ 即﹣3x2+4ax﹣1≤0恒成立，‎ ‎∴△=16a2﹣12≤0，解得﹣≤a≤‎ ‎∴实数a的取值范围是得，‎ 故选：B．‎ ‎10. 已知椭圆的左、右顶点分别为，且以线段为直径的圆与直线相切，则的离心率为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】以线段为直径的圆的圆心为坐标原点，半径为，圆的方程为，‎ 直线与圆相切，所以圆心到直线的距离等于半径，即，‎ 整理可得，即即，‎ 从而，则椭圆的离心率，‎ 故选A.‎ ‎【名师点睛】解决椭圆和双曲线的离心率的求值及取值范围问题，其关键就是确立一个关于的方程或不等式，再根据的关系消掉得到的关系式，而建立关于的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.‎ ‎11. 已知双曲线：的右顶点为，过右焦点的直线与的一条渐近线平行，交另一条渐近线于点，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由双曲线：，得，，故，所以，，渐近线方程为，不妨设的方程为，代入方程，解得，所以，故选B.‎ ‎12. 设函数，曲线在点处的切线方程为，则实数的值为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】函数f（x）=的导数为f′（x）=a+，‎ 可得y=f（x）在点（2，f（2））处的切线斜率为a+，‎ 切点为（2，2a﹣），‎ 由切线方程7x﹣4y﹣12=0，可得a+=，2a﹣=，‎ 解得a=1，b=3．‎ 故选：A．‎ 点睛：求曲线的切线方程是导数的重要应用之一，用导数求切线方程的关键在于求出切点 及斜率，其求法为：设是曲线上的一点，则以的切点的切线方程为：．若曲线在点的切线平行于轴（即导数不存在）时，由切线定义知，切线方程为．‎ ‎13. 设分别为双曲线 的左、右焦点，双曲线上存在一点使得，，则该双曲线的离心率为（ ）‎ A. B. C. D. 3‎ ‎【答案】C ‎【解析】由双曲线的定义可得，‎ ‎||PF1|﹣|PF2||=2a，‎ 由|PF1|+|PF2|=3b，|PF1|•|PF2|=，‎ 则有（|PF1|+|PF2|）2﹣4|PF1|•|PF2|=9b2﹣9ab=4a2，‎ 即有（3b﹣4a）（3b+a）=0，‎ 即有3b=4a，即9b2=16a2=9（c2﹣a2），‎ 则9c2=25a2，即有3c=5a，则e==．‎ 故选：C 点睛：解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a，b，c的方程或不等式，再根据a，b，c的关系消掉b得到a，c的关系式，建立关于a，b，c的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.‎ ‎14. 已知定义在实数集上的函数满足，且的导函数，则不等式的解集为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】设t=lnx，‎ 则不等式f（lnx）＞3lnx+1等价为f（t）＞3t+1，‎ 设g（x）=f（x）﹣3x﹣1，‎ 则g′（x）=f′（x）﹣3，‎ ‎∵f（x）的导函数f′（x）＜3，‎ ‎∴g′（x）=f′（x）﹣3＜0，此时函数单调递减，‎ ‎∵f（1）=4，‎ ‎∴g（1）=f（1）﹣3﹣1=0，‎ 则当x＜1时，g（x）＞g（1）=0，‎ 即g（x）＜0，则此时g（x）=f（x）﹣3x﹣1＞0，‎ 即不等式f（x）＞3x+1的解为x＜1，‎ 即f（t）＞3t+1的解为t＜1，‎ 由lnx＜1，解得0＜x＜e，‎ 即不等式f（lnx）＞3lnx+1的解集为（0，e），‎ 故选：A．‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎15. 设，是的导函数，则__________．‎ ‎【答案】-1‎ ‎【解析】∵f（x）=sinx+2xf'（），∴f'（x）=cosx+2f'（），‎ 令x=，可得：f'（）=cos+2f'（），解得f'（）=，‎ 则f'（）=cos+2×=﹣1．‎ 故答案为：﹣1‎ ‎16. 若满足，则__________．‎ ‎【答案】-2‎ ‎【解析】∵f（x）=ax4+bx2+c，‎ ‎∴f′（x）=4ax3+2bx，‎ ‎∴f′（1）=4a+2b=2，‎ ‎∴f′（﹣1）=﹣4a﹣2b=﹣（4a+2b）=﹣2，‎ 故答案为：-2．‎ ‎17. 已知抛物线的焦点为，准线，点在抛物线上，点在准线上，若，且直线的斜率，则的面积为__________．‎ ‎【答案】‎ ‎【解析】‎ 抛物线的焦点为F（，0），准线方程为x=﹣，抛物线C：y2=6x 点M在抛物线C上，点A在准线l上，若MA⊥l，且直线AF的斜率kAF=，‎ 准线与x轴的交点为N，则AN=3=3，A（﹣，3），则M（，3），‎ ‎∴S△AMN=×6×3=9．‎ 故答案为：．‎ 点睛：在解决与抛物线有关的问题时，要注意抛物线的定义在解题中的应用。抛物线定义有两种用途：一是当已知曲线是抛物线时，抛物线上的点M满足定义，它到准线的距离为d，则|MF|＝d，可解决有关距离、最值、弦长等问题；二是利用动点满足的几何条件符合抛物线的定义，从而得到动点的轨迹是抛物线．‎ ‎18. 函数存在与直线平行的切线，则实数的取值范围为__________．‎ ‎【答案】‎ ‎【解析】f′(x)＝＋a(x>0)．∵函数f(x)＝lnx＋ax存在与直线2x－y＝0平行的切线，‎ ‎∴方程＋a＝2在区间(0，＋∞)上有解，即a＝2－在区间(0，＋∞)上有解，‎ ‎∴a<2.‎ 若直线2x－y＝0与曲线f(x)＝lnx＋ax相切，设切点为(x0,2x0)，则 解得x0＝e，a＝2－.所以2－‎ 综上，实数a的取值范围是(－∞，2－)∪(2－，2)．‎ 三、解答题 （每题12分，共60分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎19. 已知函数，且在处.‎ ‎（1）求的值；并求函数在点处的切线方程；‎ ‎（2）求函数的单调区间.‎ ‎【答案】(1) (2)增区间为 ，减区间为 ‎ ‎【解析】试题分析：（Ⅰ）先求函数的定义域，然后求导，利用导数的几何意义求切线方程．‎ ‎（Ⅱ）利用f'（x）＜0，求函数的单调递减区间．‎ 试题解析：‎ 函数的导数为，因为函数在x=1处=0，‎ 所以f'（1）=﹣2+a﹣1=0，解得a=3．‎ 所以f（x）=﹣x2+3x+1﹣lnx，，‎ 所以f（2）=﹣4+6+1﹣ln2=3﹣ln2，，‎ 所以函数f（x）在点（2，f（2））处的切线方程为，即．‎ ‎（Ⅱ）由（Ⅰ）知，‎ 由，即2x2﹣3x+1＜0，解得，即函数的增区间为（）．‎ 由，得2x2﹣3x+1＞0，解得，‎ 即函数的减区间为（0，）和（1，+∞）．‎ ‎20. 已知双曲线：.‎ ‎（1）已知直线与双曲线交于不同的两点，且，求实数的值；‎ ‎（2）过点作直线与双曲线交于不同的两点，若弦恰被点平分，求直线的方程.‎ ‎【答案】(1) m=±2 (2) 4x﹣y﹣2=0‎ ‎【解析】试题分析：（Ⅰ）分别设A，B的坐标为（x1，y1），（x2，y2），根据弦长公式即可求出，‎ ‎（Ⅱ）分别设M，N的坐标为（x3，y3），（x4，y4），可得y32﹣x32=1，y42﹣x42=1，两式相减，再由中点坐标公式和直线的斜率公式，化简整理可得MN的斜率，再由点斜式方程可得所求直线方程 试题解析：‎ 解：（Ⅰ）分别设A，B的坐标为（x1，y1），（x2，y2）‎ 由，消y可得，x2﹣4mx+2（m2﹣1）=0，‎ ‎∴x1+x2=4m，x1•x2=2（m2﹣1），‎ ‎∴|x1﹣x2|2=（x1+x2）2﹣4x1•x2=16m2﹣8（m2﹣1）=8（m2+1），‎ ‎∴|AB|=•=4，解得m=±2，‎ ‎（Ⅱ）分别设M，N的坐标为（x3，y3），（x4，y4），可得y32﹣x32=1，y42﹣x42=1，‎ 两式相减，可得（y3﹣y4）（y3+y4）=（x3﹣x4）（x3+x4），‎ 由点P（1，2）为MN的中点，‎ 可得x3+x4=2，y3+y4=4，‎ ‎∴4（y3﹣y4）=×2（x3﹣x4），∴kMN==4 经检验 即直线l的方程为y﹣2=4（x﹣1），即为4x﹣y﹣2=0‎ ‎21. 已知抛物线与直线相交于.‎ ‎（1）求证：；‎ ‎（2）当的面积等于时，求的值.‎ ‎【答案】(1) 见解析 (2) ‎ ‎【解析】试题分析：证明可有两种思路：证,取中点,证 求的值，关键是利用面积建立关于的方程，求的面积也有两种思路：利用 ‎，设,,直线和轴交点为，利用 ‎.‎ 解析：由方程 消去后，整理得 设,，由韦达定理 在抛物线上，‎ 设直线与轴交点为，又显然 令则,即 ‎,解得 点睛：本题考查了直线与抛物线的关系，在求三角形面积时可以采用分割的方法，沿着轴分割成两个三角形，这样在计算两个三角形面积时有公共底，高就可以转化为直线与抛物线两交点纵坐标的差，再依据直线方程与抛物线方程联立，求得两交点纵坐标的差。‎ ‎22. 已知椭圆的上下两个焦点分别为，过点与轴垂直的直线交椭圆于 两点，的面积为，椭圆的离心率为.‎ ‎（1）求椭圆的标准方程；‎ ‎（2）已知为坐标原点，直线与轴交于点，与椭圆交于两个不同的点，若存在实数，使得，求的取值范围.‎ ‎【答案】(1) (2) （﹣2，﹣1）∪（1，2）∪{0}‎ ‎【解析】（Ⅰ）根据题目条件，由椭圆焦点坐标和对称性计算的面积，建立等式关系，结合关系式，离心率计算公式，问题可得解；（Ⅱ）由题意，可分直线是否过原点，对截距进行分类讨论，再利用椭圆对称性、向量共线、直线与椭圆有交点等性质、条件进行运算即可.‎ 试题解析：（Ⅰ）根据已知椭圆的焦距为，当时，，‎ 由题意的面积为，‎ 由已知得，∴，∴，‎ ‎∴椭圆的标准方程为．‎ ‎（Ⅱ）若，则，由椭圆的对称性得，即，‎ ‎∴能使成立．‎ 若，由，得，‎ 因为，，共线，所以，解得．　‎ 设，，由 得，‎ 由已知得，即，‎ 且，，‎ 由，得，即，∴，‎ ‎∴，即．‎ 当时，不成立，∴，‎ ‎∵，∴，即，‎ ‎∴，解得或．‎ 综上所述，的取值范围为．‎ 点睛：此题主要考查椭圆方程及其性质，直线与椭圆位置关系，平面向量在解析几何中的应用等有关方面的知识，属于中高档题型，也是高频考点.根据题意，在（Ⅰ）中联立椭圆方程、离心率、三角形的面积即求得椭圆方程，必要时可画草图辅助思考，在问题（Ⅱ）中联立椭圆与直线方程消去，由韦达定理求得直线与椭圆交点的横坐标和与积，再利用平面向量的共线关系，从而求出待定系数的取值范围.‎ ‎23. 设函数，其中为实数.‎ ‎（1）已知函数是奇函数，直线是曲线的切线，且，，求直线的方程；‎ ‎（2）讨论的单调性.‎ ‎【答案】(1) 6x+3y﹣1=0或2x+y+5=0 (2)见解析 ‎【解析】试题分析：（1）根据函数g（x）=f（x）﹣f′（x）是奇函数可求出a的值，然后根据l1⊥l2可求出l1的斜率，从而可求出切点坐标，求出切线方程；‎ ‎（2）先求函数f（x）的导函数f′（x），再解不等式f′（x）＞0和f′（x）＜0即可得函数的单调区间，本题需讨论a与﹣和0的大小关系．‎ 试题解析：‎ 解：（1）∵，‎ ‎∴f′（x）=ax2﹣x﹣（a+1）‎ 则g（x）=f（x）﹣f′（x）=﹣ax2+x+（a+1）=‎ ‎∵函数g（x）=f（x）﹣f′（x）是奇函数∴+a=0即a=﹣则f′（x）=﹣x2﹣x﹣‎ ‎∵l1⊥l2，l2：x﹣2y﹣8=0‎ ‎∴l1的斜率为﹣2，即f′（x）=﹣x2﹣x﹣=﹣2解得x=1或﹣3‎ 即切点为（1，﹣）或（﹣3，1）‎ ‎∴直线l1的方程为6x+3y﹣1=0或2x+y+5=0‎ ‎（2）f′（x）=ax2﹣x﹣（a+1）=（ax﹣a﹣1）（x+1）‎ 当a=0时，f′（x）=﹣x﹣1，当x∈（﹣∞，﹣1）时，f′（x）＞0，当x∈（﹣1，+∞）时，f′（x）＜0‎ ‎∴函数f（x）的单调增区间为（﹣∞，﹣1），单调递减区间为（﹣1，+∞）‎ 当a＞0时，当x∈（﹣∞，﹣1）时，f′（x）＞0，当x∈（﹣1，1+）时，f′（x）＜0，当x∈（1+，+∞）时，f′（x）＞0‎ ‎∴函数f（x）的单调增区间为（﹣∞，﹣1），（1+，+∞）单调递减区间为（﹣1，1+）‎ 当﹣＜a＜0时，当x∈（﹣∞，1+）时，f′（x）＜0，当x∈（1+，﹣1）时，f′（x）＞0，当x∈（﹣1，+∞）时，f′（x）＜0‎ ‎∴函数f（x）的单调增区间为（1+，﹣1）单调递减区间为（﹣∞，1+），（﹣1，+∞）‎ 当a=﹣时，f′（x）≤0恒成立，即函数单调递减区间为（﹣∞，+∞）‎ 当a＜﹣时，当x∈（﹣∞，﹣1）时，f′（x）＜0，当x∈（﹣1，1+）时，f′（x）＞0，当x∈（1+，+∞）时，f′（x）＜0‎ ‎∴函数f（x）的单调增区间为（﹣1，1+）单调递减区间为（﹣∞，﹣1），（1+，+∞）‎ 点睛：导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出 ，本专题在高考中的命题方向及命题角度 从高考来看，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系． (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用．‎