- 1.00 MB
- 2021-06-22 发布
文科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.在复平面内,复数(是虚数单位)的共轭复数对应的点位于( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
3.甲、乙两棉农,统计连续五年的面积产量(千克/亩)如下表:
棉农甲
68
72
70
69
71
棉农乙
69
71
68
68
69
则平均产量较高与产量较稳定的分别是( )
A.棉农甲,棉农甲 B.棉农甲,棉农乙 C.棉农乙,棉农甲 D.棉农乙,棉农乙
4.已知等差数列满足,则有( )
A. B. C. D.
5.已知函数则( )
A.32 B.16 C. D.
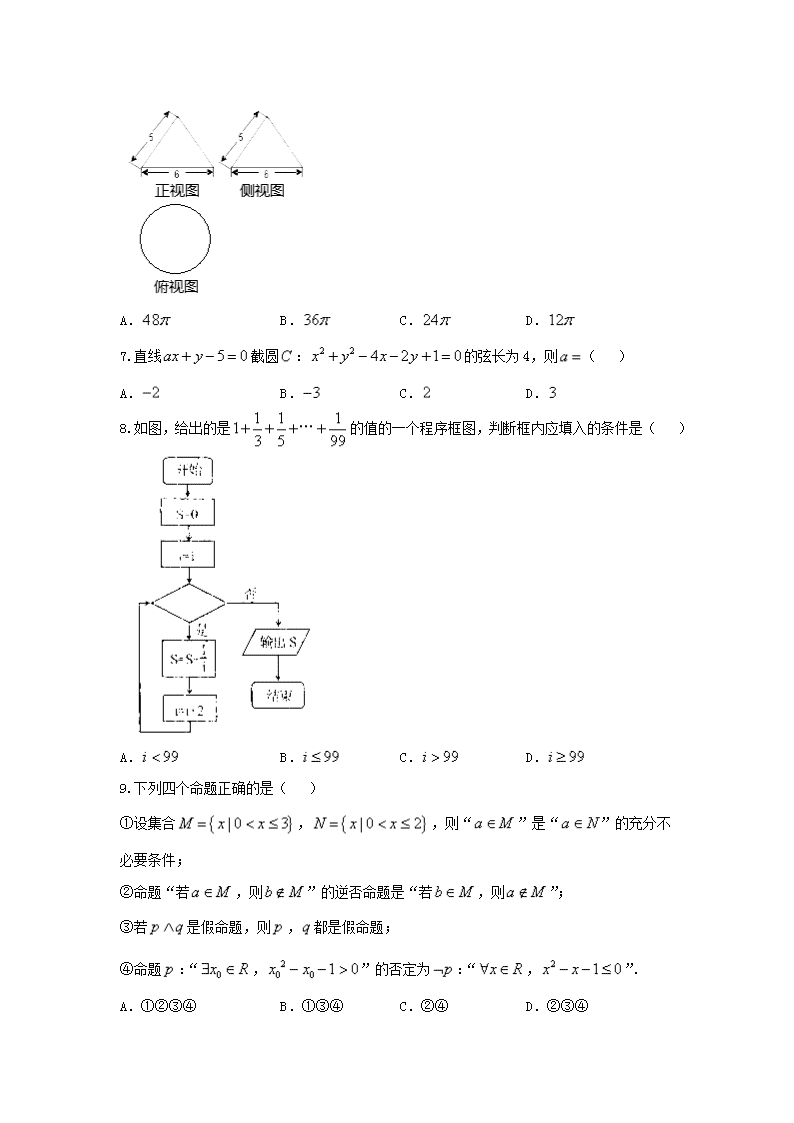
6.有一个几何体的正视图、侧视图、俯视图如图所示,则该几何体的表面积为( )
A. B. C. D.
7.直线截圆:的弦长为4,则( )
A. B. C. D.
8.如图,给出的是的值的一个程序框图,判断框内应填入的条件是( )
A. B. C. D.
9.下列四个命题正确的是( )
①设集合,,则“”是“”的充分不必要条件;
②命题“若,则”的逆否命题是“若,则”;
③若是假命题,则,都是假命题;
④命题:“,”的否定为:“,”.
A.①②③④ B.①③④ C.②④ D.②③④
10.已知在三棱锥中,,,,平面平面,若三棱锥的顶点在同一个球面上,则该球的表面积为( )
A. B. C. D.
11.已知椭圆:,点,,分别为椭圆的左顶点、上顶点、左焦点,若,则椭圆的离心率是( )
A. B. C. D.
12.设,分别是定义在上的奇函数和偶函数,当时,,且,则不等式的解集是( )
A. B. C.D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知向量,满足,,且(),则 .
14.设,满足约束条件则的取值范围为 .
15.已知等差数列的前项和为,且满足,则数列的公差是 .
16.某中学为了解学生的数学学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图,根据频率分布直方图,推测这3000名学生在该次数学考试中成绩小于60分的学生数是 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. (本小题满分12分)
在中,角,,的对边分别为,,,已知,,且
.
(1)求角的大小;
(2)求的面积.
18. (本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(1)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(2)从甲已抽取的8次预赛中随机抽取两次成绩,求这两次成绩中至少有一次高于90的概率.
19. (本小题满分12分)
已知在四棱锥中,底面是矩形,且,,平面,、分别是线段、的中点.
(1)证明:;
(2)若,求点到平面的距离.
20. (本小题满分12分)
如图,已知椭圆的中心在坐标原点,焦点在轴上,它的一个顶点为,且离心率等于,过点的直线与椭圆相交于不同两点,,点在线段上.
(1)求椭圆的标准方程;
(2)设,若直线与轴不重合,试求的取值范围.
21. (本小题满分12分)
已知函数.
(1)当时,求函数的单调递增区间;
(2)在区间内至少存在一个实数,使得成立,求实数的取值范围.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22. (本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)写出曲线的直角坐标方程;
(2)已知直线与轴的交点为,与曲线的交点为,,若的中点为,求的长.
23. (本小题满分10分)选修4-5:不等式选讲
设函数,.
(1)当时,求不等式的解集;
(2)若对恒成立,求的取值范围.
遵义市南白中学2016-2017高三第四次联考试卷文科数学答案
一、选择题
1-5: 6-10: 11、12:
二、填空题
13.2 14.3 15.2 16.600
三、解答题
17.解:(1)∵,由,得,
∴,
整理得,
解得,
∴.
18.解:(1)甲参加比较合适,理由如下:
,
,
,
,
∵,,
∴甲的成绩比较稳定,派甲参加比较合适.
(2)抽取2次成绩可能结果有:,,,,,,,,,,,,,,,,,,,,,
,,,,,,共有28种.
两次成绩中至少有一次高于90的有:,,,,,,,,,,,,共有13种.
则这两次成绩中至少有一次高于90的概率为.
19.(1)证明:连接,则,,
又,∴,∴,
又平面,∴,又,
∴平面,
又平面,
∴.
(2)解:,
∵,
∴,
解得,
即点到平面的距离为.
20.解:(1)设椭圆的标准方程是,
由于椭圆的一个顶点是,故,根据离心率是,得,解得,
所以椭圆的标准方程是.
(2)设,,,
设直线的方程为,与椭圆方程联立消去得,
根据韦达定理得,,
由,得,整理得,把上面的等式代入得,
又点在直线上,所以,于是有,
,由,得,所以.
综上所述,.
21.解:(1)当时,,
当,得或,
所以函数在与上为增函数.
(2)(),
当,即时,,在上为增函数,
故,所以,,这与矛盾;
当,即时,
若,;若,,
所以时,取最小值,
因此有,即,
解得,这与矛盾;
当,即时,,在上为减函数,所以,
所以,解得,这符合.
综上所述,的取值范围为.
22.解:(1)曲线的直角坐标方程为.
(2)的坐标为,将的参数方程代入曲线的直角坐标方程得:,
设点,,对应的参数分别为,,,则,,
,
∴的长为.
23.解:(1)等价于或或
解得或.
故不等式的解集为或.
(2)因为(当时等号成立),
所以,
由题意得,解得或.