2017-2018学年湖南省桃江县第一中学高二上学期入学考试数学试题 8页

‎2017-2018学年湖南省桃江县第一中学高二上学期入学考试数学试题 ‎ 时间：120分钟　满分150　命题人：邓宏坤 　审题人：彭巨洪 一、选择题：本大题共12小题，每小题5分，共60分,在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.己知，那么角是 ‎ A.第一或第二象限角 B.第二或第三象限角 ‎ C.第三或第四象限角 D.第一或第四象限角2.从编号为1～50的50枚最新研制的某种型号的弹道导弹中随机抽取5枚来进行发射试验，若采用每部分选取的号码间隔一样的系统抽样方法，则所选取的5枚导弹的编号可能是 A. 3、13、23、33、43 B. 5、10、15、20、25‎ ‎ C.1、2、3、4、5 D. 2、4、8、16、32‎ ‎3.如果执行右边的程序框图，那么输出的 ‎ A. 22 B.46 C. 94 D. 190‎ ‎4.在区间（0，3]上随机取一个数x，则事件“0≤log2x ≤1”发生的概率为 ‎ A． B． C． D．‎ ‎5.△ABC的内角A、B、C的对边分别为a、b、c．已知a=，b=3，cosA=，则 c=（　　）‎ ‎ A．3 B． C． D．2‎ ‎6．若x、y满足约束条件，则z=3x﹣2y的最小值为（　　）‎ ‎ A． B．﹣ C．﹣5 D．5‎ ‎7．在各项不为零的等差数列中，，数列是等比数列，且则 ‎ ‎ A． B． C． D． ‎ ‎8.由函数的图象得到的图象，需要将的图象 ‎(A)向左平移个单位 （B)向右平移个单位 ‎(C)向左平移个单位 （D)向右平移个单位 ‎9、已知直线x+(m2-m)y=4m-1与直线2x-y-5=0垂直,则m的值为 ‎ A.-1 B.2 C.-1或2 D.1‎ ‎10.已知: 、是不共线向量，，，且，则的值为 ‎ A. 8 B.3 C.-3 D.-8‎ ‎11.在△ABC中，已知D是AB边上一点， =2，，则实数λ=‎ ‎ A．﹣ B．﹣ C． D．‎ ‎12.函数的图象与直线有且仅有两个不同的交点，则的取值范围是 ‎ A. B. C. D).[1.3]‎ 二、填空题:本大题共4小题.每小题5分，共20分.‎ ‎13．化简的结果为　 　;‎ ‎14.不等式的解集为______;‎ ‎15.已知向量，向量,则向量在向量方向上的投影为______;‎ ‎16．给定两个长度为2且互相垂直的平面向量和，点C在以O为圆心的圆弧上变动，若，其中x，y∈R，则x+y的最大值是　　．‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分10分）已知角α终边上一点P（﹣4，3 ），求的值。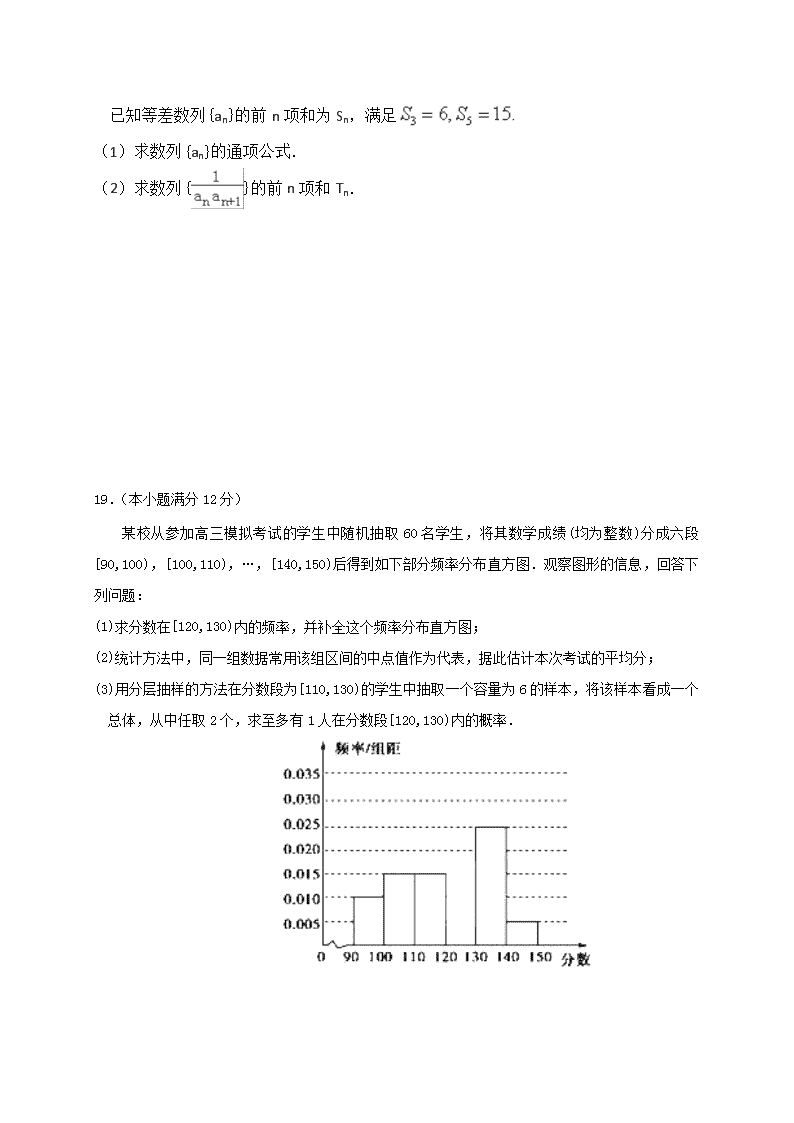‎ 18． ‎（本小题满分12分）‎ ‎ 已知等差数列{an}的前n项和为Sn，满足 ‎（1）求数列{an}的通项公式．‎ ‎（2）求数列{}的前n项和Tn．‎ ‎19．（本小题满分12分）‎ 某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段[90,100)，[100,110)，…，[140,150)后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：‎ (1) 求分数在[120,130)内的频率，并补全这个频率分布直方图； ‎ (2) 统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；‎ ‎(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2个，求至多有1人在分数段[120,130)内的概率．‎ 20、 ‎(本小题满分10分)‎ 设△ABC中的内角A,B,C的边分别为a,b,c,若c =,sinB=2sinA,C=.‎ ‎(Ⅰ)求a,b的值;‎ ‎(Ⅱ)求△ABC的面积.‎ ‎21．．‎ ‎（2）将的图象向左移，再将各点横坐标伸长为原来的2倍，纵坐标不变，得y=g（x），若关于g（x）+m=0在区间上的有且只有一个实数解，求m的范围．‎ ‎2017年高二入学考试数学试卷参考答案 一、选择题：[]‎ ‎1-5：BACCD, 6-10:CDBCD, 11-12:DB.‎ 二、 填空题:‎ 13. sin40°; 14.（-1，）； 15.-1; 16..‎ 三、解答题 ‎17.（本小题满分10分）‎ 解：角α终边上一点P（﹣4，3 ），‎ ‎∴tanα==﹣；‎ ‎∴====tanα=﹣．‎ ‎18.（本小题满分12分）‎ 解：（1）设等差数列{an}的公差为d，∵S3=6，S5=15．‎ ‎∴3a1+d=6，5a1+d=15，‎ 解得a1=d=1．‎ ‎∴an=1+n﹣1=n．‎ ‎（2）由an=n，，‎ 则．‎ ‎19．（本小题满分12分）‎ ‎(1)分数在[120,130)内的频率为：1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3.‎ ＝＝0.03，补全后的直方图如下：‎ ‎(2)平均分为：95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121.‎ ‎(3)由题意，[110,120)分数段的人数为：60×0.15＝9人，[]‎ ‎[120,130)分数段的人数为：60×0.3＝18人．‎ ‎∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，‎ ‎∴需在[110,120)分数段内抽取2人，并分别记为m，n；‎ 在[120,130)分数段内抽取4人并分别记为a，b，c，d；‎ 设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A，‎ 则基本事件有：(m，n)，(m，a)，(m，b)，(m，c)，(m，d)，(n，a)，(n，b)，‎ ‎(n，c)，(n，d)，(a，b)，(a，c)，(a，d)，(b，c)，(b，d)，(c，d)共15种．‎ 事件A包含的基本事件有：(m，n)，(m，a)，(m，b)，(m，c)，(m，d)，(n，a)，‎ ‎(n，b)，(n，c)，(n，d)共9种．‎ ‎∴P(A)＝＝ ‎20. （本小题满分12分）‎ ‎21. （本小题满分12分）‎ 解：（1）=（sin2x，cos2x），=（cos2x，﹣cos2x），‎ ‎∴f（x）=•+‎ ‎=sin2xcos2x﹣cos22x+=sin4x﹣cos4x﹣+=﹣cos（4x+）,‎ ‎（2）由（1）知，f（x）=sin4x﹣cos4x=sin（4x﹣），‎ 将f（x）的图象向左平移个单位，得y=sin[4（x+）﹣]=sin（4x+）的图象；再将y各点横坐标伸长为原来的2倍，纵坐标不变，得y=sin（2x+）的图象；则y=g（x）=sin（2x+）；‎ 当x∈时，2x+∈[，]，‎ 画出函数g（x）的图象，如图所示；‎ 则g（x）+m=0在区间上的有且只有一个实数解时，应满足﹣≤﹣m＜或﹣m=1；‎ 即﹣＜m≤，或m=﹣1．‎ 22. ‎（本小题满分12分）‎ 解：假设存在锐角，使同时成立，则 ‎，则，即 又因为，则为方程 的两根。，‎