- 1.07 MB
- 2021-06-21 发布
桃江一中2019年上学期高二期中考试试卷
高二数学文科试题
命题人:曹军 审题人:周亦文
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={1,2},B={2,4},则A∪B=( ).
A.{2} B.{1,2,2,4} C.{1,2,4} D.∅
2.函数f(x)=+log4(x+1)的定义域是( )
A.(-1,+∞) B.[-1,1)(1,4] C.(-1,4) D.(-1,1)(1,4]
3.若0<m<n<1,则( )
A.3n<3m B.logm3<logn3 C.log4m<log4n D.
4.二次函数f(x)=ax2+bx+c(xR)的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
y
6
m
-4
-6
-6
-4
n
6
由此可以判断方程ax2+bx+c=0的两个根所在的区间是( )
A.(-3,-1)和(2,4) B.(-3,-1)和(-1,1)
C.(-1,1)和(1,2) D.(-∞,-3)和(4,+∞)
5.过点且平行于直线的直线方程为( )
A. B. C. D.
6.已知圆内一点P(2,1),则过P点最短弦所在的直线方程是 ( )
A
B
A1
B1
C
C1
正视图
侧视图
俯视图
A. B. C. D.
7.如右图为一个几何体的三视图,
其中俯视图为正三角形,A1B1=2,
AA1=4,则该几何体的表面积为( )
A.6+ B.24+ C.24+2 D.32
8.如图是正方体的平面展开图,则在这个正方体中与的 位置关系为( )
A、相交 B、平行
C、异面而且垂直 D、异面但不垂直
9.已知偶函数f(x)=loga|x-b|在(-∞,0)上单调递增, 则f(a+1)与f(b+2)的大小关系是( )
A.f(a+1)≥f(b+2) B.f(a+1)<f(b+2)
C.f(a+1)≤f(b+2) D.f(a+1)>f(b+2)
10.若曲线C的参数方程为(θ为参数),直线l的方程为x-3y+2=0,则曲线C上到直线l距离为的点的个数为( )
A.1 B.2 C.3 D.4
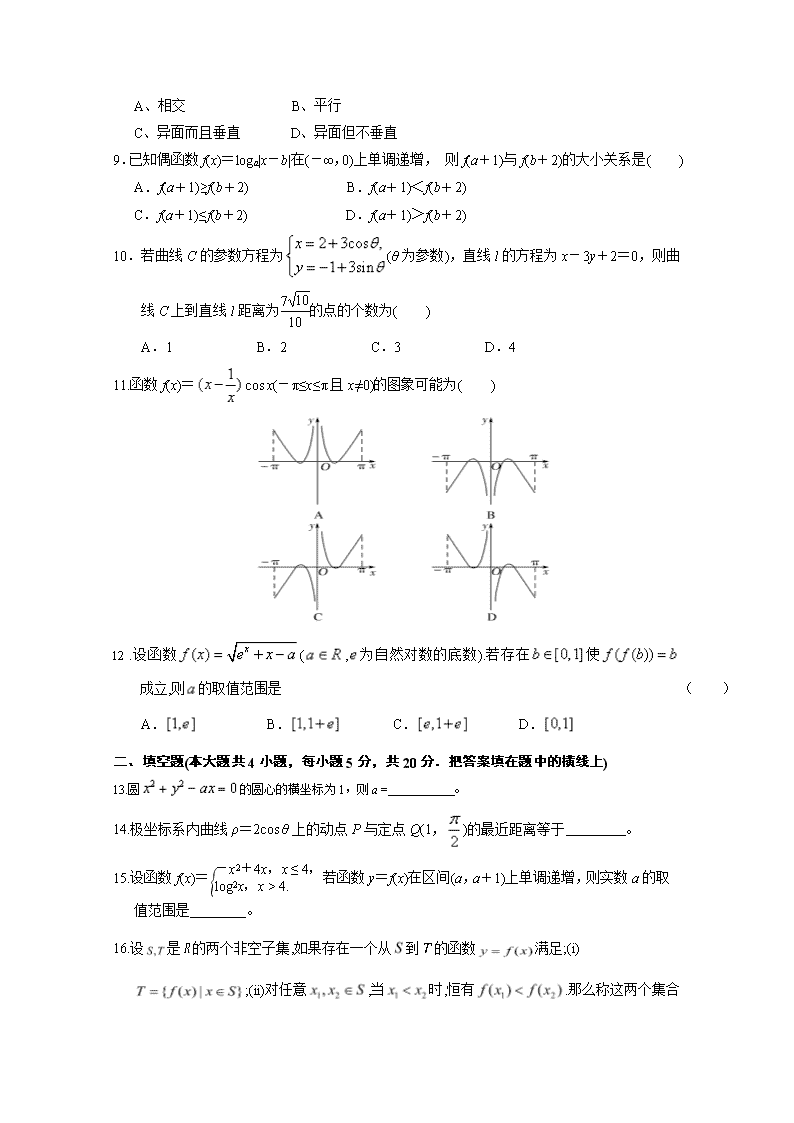
11.函数f(x)=cos x(-π≤x≤π且x≠0)的图象可能为( )
12 .设函数(,为自然对数的底数).若存在使成立,则的取值范围是 ( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.圆的圆心的横坐标为1,则a = 。
14.极坐标系内曲线ρ=2cos θ上的动点P与定点Q(1,)的最近距离等于 。
15.设函数f(x)=若函数y=f(x)在区间(a,a+1)上单调递增,则实数a的取值范围是________。
16.设是的两个非空子集,如果存在一个从到的函数满足;(i);(ii)对任意,当时,恒有
.那么称这两个集合“保序同构”.现给出以下3对集合:
① ②
③
其中,“保序同构”的集合对的序号是____________(写出所有“保序同构”的集合对的序号) 。
三、解答题(本大题共六个小题,共70分)(要求写出文字说明,证明过程或计算步骤)
17(12分)设,求实数和的值.
18(12分)已知函数是定义在上的偶函数,且.
(1) 求函数的解析式;
(2) 解不等式.
19(12分)已知圆经过点,和直线相切,且圆心在直线上.
(1) 求圆的方程;
(2) 已知直线经过原点,并且被圆截得的弦长为2,求直线的方程.
20(12分)如图,四棱锥的底面是矩形,分别是,的中点,且.
(1) 求证:;
(2) 求证:平面.
21(12分)已知函数.
(1) 讨论的单调性;
(2) 当有最大值,且最大值大于时,求实数的取值范围.
22(10分)在平面直角坐标系中,以原点为极点,轴的非负半轴为极轴,建立极坐标系,曲线的极坐标方程为,直线的参数方程为,
(为参数,)
(1) 若,求的普通方程,直接写出的直角坐标方程;
若与有两个不同的交点,且为的中点,求.