2018-2019学年河南省洛阳市第一中学高一12月月考数学试题 8页

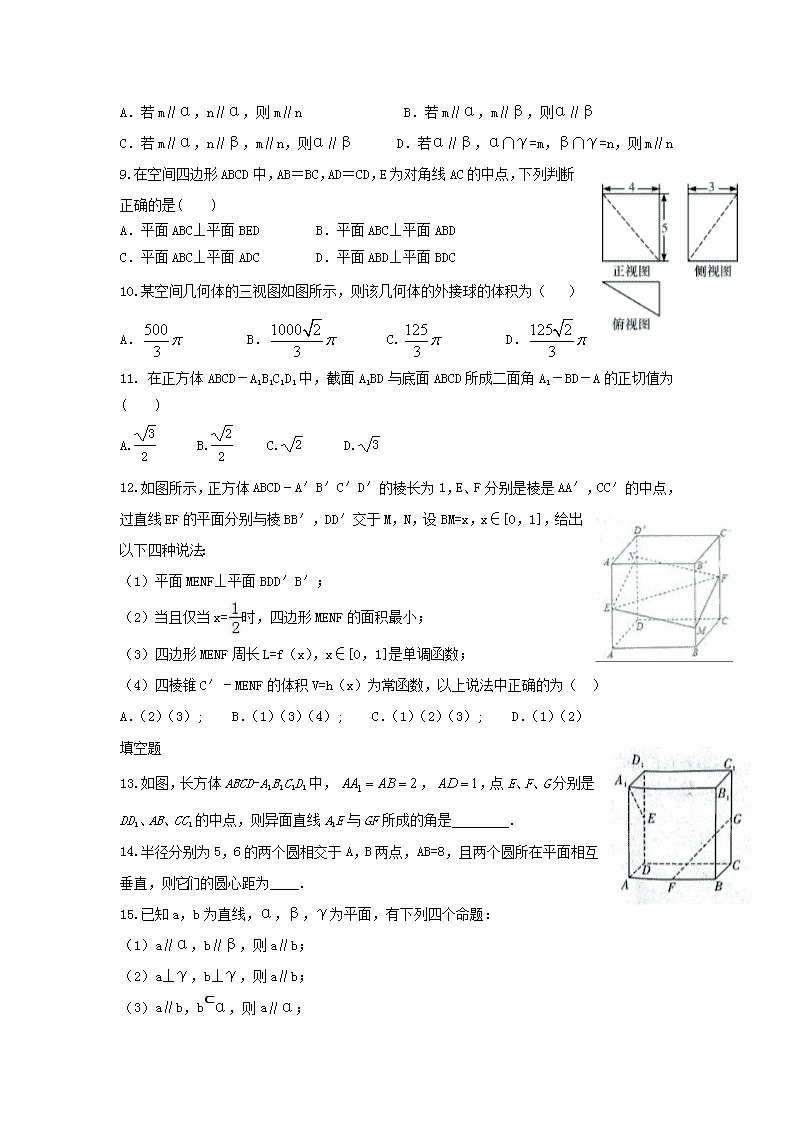
‎ ‎ ‎2018-2019学年河南省洛阳市第一中学高一12月月考数学试题 ‎1. 如图，正方形的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是（ ）‎ A. 6 B. 8 C. D. ‎ ‎2.一个三棱锥的三视图如右图所示，则这个三棱锥的表面积为（ ）‎ A． B． C. D． ‎ ‎3若两个平面互相平行，则分别在这两个平行平面内的两条直线（　　）‎ A．平行 B．异面 C．相交 D．平行或异面 ‎4.已知函数的定义域为(－1,0)，则函数的定义域为(　　)‎ A．(-1,1) B．(-1，-) C． (，1) D．(-1,0)‎ ‎5.已知定义域为R的函数f(x)满足，当时f(x)单调递减且，则实数a的取值范围是( )‎ A.[2，+ ∞) B.[0，4]‎ C. (－∞，0) D.(－∞，0)∪[4，+∞) ‎ ‎6.如图，在正四棱柱ABCD﹣A1B1C1D1中，E、F分别是AB1、BC1的中点，则以下结论中不成立的是（）‎ A．EF与BB1垂直 B．EF与BD垂直 ‎ C．EF与CD异面 D．EF与A1C1异面 ‎7.设直三棱柱ABC-A1B1C1的体积为V，点P、Q分别在侧棱AA1、CC1上，且PA=QC1，则四棱锥B-APQC的体积为（ ）．‎ A． B． C． D．‎ ‎8.设m，n为两条不同的直线，α，β，γ为三个不同的平面，则下列四个命题中为真命题的是（　　） ‎ A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥β ‎ C．若m∥α，n∥β，m∥n，则α∥β D．若α∥β，α∩γ=m，β∩γ=n，则m∥n ‎9.在空间四边形ABCD中，AB＝BC，AD＝CD，E为对角线AC的中点，下列判断正确的是(　　)‎ A．平面ABC⊥平面BED B．平面ABC⊥平面ABD C．平面ABC⊥平面ADC D．平面ABD⊥平面BDC ‎10.某空间几何体的三视图如图所示，则该几何体的外接球的体积为（ ）‎ A． B． C. D．‎ ‎11. 在正方体ABCD－A1B1C1D1中，截面A1BD与底面ABCD所成二面角A1－BD－A的正切值为(　　)‎ A. B. C. D. 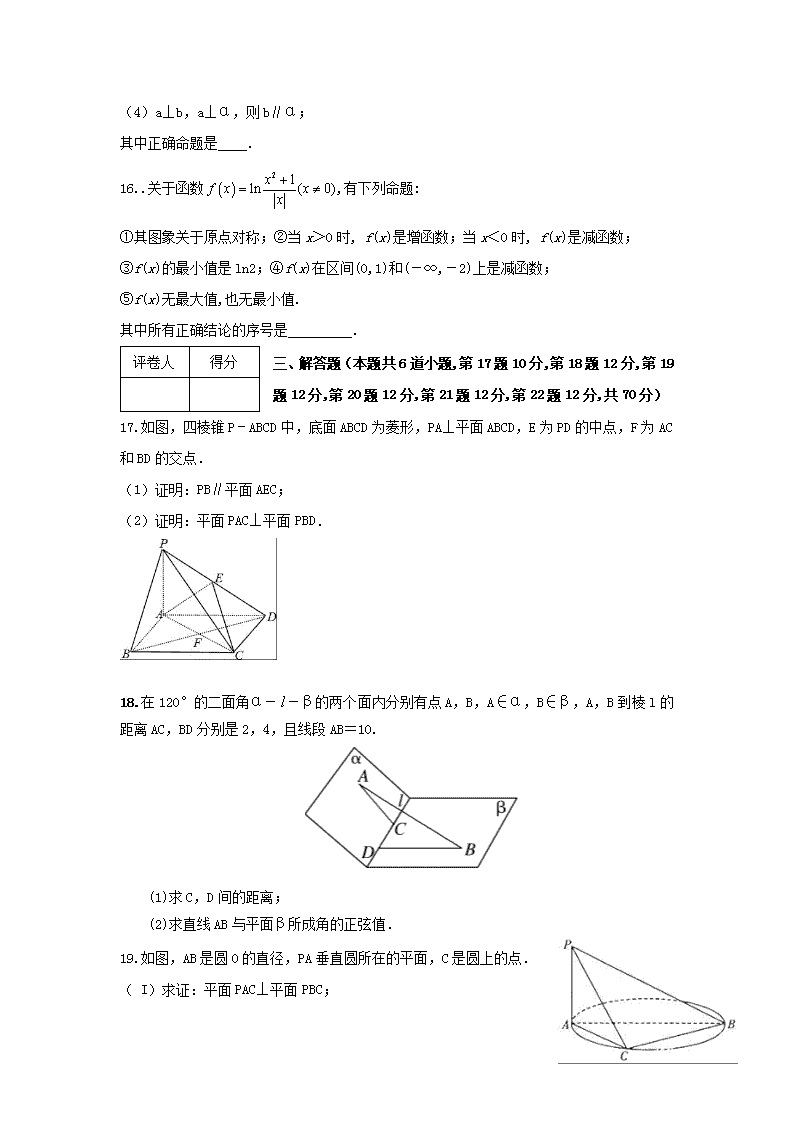‎12.如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E、F分别是棱是AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，设BM=x，x∈[0，1]，给出以下四种说法：‎ ‎（1）平面MENF⊥平面BDD′B′；‎ ‎（2）当且仅当x=时，四边形MENF的面积最小；‎ ‎（3）四边形MENF周长L=f（x），x∈[0，1]是单调函数；‎ ‎（4）四棱锥C′﹣MENF的体积V=h（x）为常函数，以上说法中正确的为（　）‎ A．（2）（3）; B．（1）（3）（4）; C．（1）（2）（3）; D．（1）（2）‎ 填空题 ‎13.如图，长方体ABCD-A1B1C1D1中，，，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是 ．‎ ‎14.半径分别为5，6的两个圆相交于A，B两点，AB=8，且两个圆所在平面相互垂直，则它们的圆心距为　　．‎ ‎15.已知a，b为直线，α，β，γ为平面，有下列四个命题：‎ ‎（1）a∥α，b∥β，则a∥b； ‎ ‎（2）a⊥γ，b⊥γ，则a∥b；‎ ‎（3）a∥b，b⊂α，则a∥α；‎ ‎（4）a⊥b，a⊥α，则b∥α；‎ 其中正确命题是　　．‎ ‎16..关于函数,有下列命题:‎ ‎①其图象关于原点对称；②当x＞0时, f(x)是增函数；当x＜0时, f(x)是减函数；‎ ‎③f(x)的最小值是ln2；④f(x)在区间(0,1)和(－∞,－2)上是减函数；‎ ‎⑤f(x)无最大值,也无最小值.‎ 其中所有正确结论的序号是 ．‎ 评卷人 得分 三、解答题（本题共6道小题,第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共70分）‎ ‎17.如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥平面ABCD，E为PD的中点，F为AC和BD的交点．‎ ‎（1）证明：PB∥平面AEC；‎ ‎（2）证明：平面PAC⊥平面PBD．‎ ‎18.在120°的二面角α－－β的两个面内分别有点A，B，A∈α，B∈β，A，B到棱l的距离AC，BD分别是2，4，且线段AB＝10.‎ ‎(1)求C，D间的距离；‎ ‎(2)求直线AB与平面β所成角的正弦值．‎ ‎19.如图，AB是圆O的直径，PA垂直圆所在的平面，C是圆上的点．‎ ‎（ I）求证：平面PAC⊥平面PBC；‎ ‎（ II）若AC=1，PA=1，求圆心O到平面PBC的距离．‎ ‎20.如图，C、D是以AB为直径的圆上两点，AB=2AD=2，AC=BC，F 是AB上一点，且AF=AB，将圆沿直径AB折起，使点C在平面ABD的射影E在BD上，已知：, ‎ ‎（1）求证：AD⊥平面BCE；‎ ‎（2）求三棱锥A﹣CFD的体积．‎ ‎21.如图，在四棱锥中P﹣ABCD，AB=BC=CD=DA，∠BAD=60°，AQ=QD，△PAD是正三角形．‎ ‎（1）求证：AD⊥PB；‎ ‎（2）已知点M是线段PC上，MC=λPM，且PA∥平面MQB，求实数λ的值．‎ ‎22.已知函数.‎ ‎（1）解不等式；‎ ‎（2）若函数，其中为奇函数，为偶函数，若不等式对任意恒成立，求实数的取值范围.‎ 参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B D C B D C D A D C C ‎13. ;14. ;‎ ‎15. ② ; 16. ③④ ;‎ ‎17. 【解答】解：（1）证明：连接EF，‎ ‎∵四边形ABCD是菱形，‎ ‎∴F是BD的中点，又E是PD的中点，‎ ‎∴PB∥EF，又EF⊂平面AEC，PB⊄平面AEC， ‎ ‎∴PB∥平面AEC；‎ ‎（2）∵PA⊥平面ABCD，BD⊂平面ABCD，‎ ‎∴PA⊥BD，‎ ‎∵四边形ABCD是菱形，∴BD⊥AC，‎ 又AC⊂平面PAC，PA⊂平面PAC，AC∩PA=A， ‎ ‎∴BD⊥平面PAC，又∵BD⊂平面PBD，‎ ‎∴平面PAC⊥平面PBD．‎ ‎18.① ②‎ ‎19. 【解答】解：（1）证明：由AB是圆的直径得AC⊥BC，‎ 由PA⊥平面ABC，BC⊂平面ABC，得PA⊥BC ‎∴BC⊥平面PAC，…‎ 又∴BC⊂平面PBC，‎ 所以平面PAC⊥平面PBC…‎ ‎（2）过A点作AD⊥PC于点D，则由（1）知AD⊥平面PBC，…‎ 连BD，取BD的中点E，连OE，则OE∥AD，‎ 又AD⊥平面PBCOE⊥平面PBC，‎ 所以OE长就是O到平面PBC的距离．…‎ 由中位线定理得…‎ ‎20. 解答： （1）证明：依题AD⊥BD，‎ ‎∵CE⊥平面ABD，∴CE⊥AD，‎ ‎∵BD∩CE=E，‎ ‎∴AD⊥平面BCE．‎ ‎（2）由（2）知AD∥EF，AD⊥ED，‎ 且ED=BD﹣BE=1，‎ ‎∴F到AD的距离等于E到AD的距离为1．‎ ‎∴S△FAD==．‎ ‎∵CE⊥平面ABD，‎ ‎∴VA﹣CFD=VC﹣AFD===．‎ ‎21. 【解答】证明：（1）如图，连结BD，由题意知四边形ABCD为菱形，∠BAD=60°，‎ ‎∴△ABD为正三角形，‎ 又∵AQ=QD，∴Q为AD的中点，∴AD⊥BQ，‎ ‎∵△PAD是正三角形，Q为AD中点，‎ ‎∴AD⊥PQ，又BQ∩PQ=Q，∴AD⊥平面PQB，‎ 又∵PB⊂平面PQB，∴AD⊥PB．‎ 解：（2）连结AC，交BQ于N，连结MN，‎ ‎∵AQ∥BC，∴，‎ ‎∵PN∥平面MQB，PA⊂平面PAC，‎ 平面MQB∩平面PAC=MN，‎ ‎∴根据线面平行的性质定理得MN∥PA，‎ ‎∴，‎ 综上，得，∴MC=2PM，∵MC=λPM，∴实数λ的值为2．‎ ‎22. 解：（1）设t=2x，由f（x）＞16﹣9×2x得：t﹣t2＞16﹣9t，‎ 即t2﹣10t+16＜0 ‎ ‎∴2＜t＜8，即2＜2x＜8，∴1＜x＜3‎ ‎∴不等式的解集为（1，3）．‎ ‎（2） 由题意得 解得. ‎ ‎2ag（x）+h（2x）≥0，即，对任意x∈[1，2]恒成立，‎ 又x∈[1，2]时，令，‎ 在上单调递增，‎ 当时，有最大值，‎ 所以