数学理·广东省清远市第三中学2016-2017学年高二上学期第一次月考理数试题 Word版含解析x 16页

全*品*高*考*网， 用后离不了！广东省清远市第三中学2016-2017学年高二上学期第一次月考 理数试题 ‎ 第Ⅰ卷（共60分）‎ 一、选择题（共12小题，共60分）‎ ‎1．平面截球的球面所得圆的半径为，球心到平面的距离为，则球的表面积为（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】‎ 试题分析：由题球心到平面的距离为，可得；，则球的表面积为；,，故选B 考点：球的截面性质及表面积．‎ ‎2．已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形，则此三棱锥的体积等于（ ）‎ A． ‎ B． C． D．‎ ‎【答案】C ‎【解析】‎ 试题分析:由三视图，则左（侧）视图可推知底面的高，俯视图可推知底面再结合主视图，‎ 则三棱锥的底面积为；， 而三棱锥的高为；‎ 得： ,故选C 考点：三视图与几何体的体积．‎ ‎3．已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形，则此三棱锥的体积等于（ ）‎ A． ‎ B． C． D． ‎ ‎【答案】C ‎【解析】‎ 试题分析:由三视图，则左（侧）视图可推知底面的高，俯视图可推知底面再结合主视图，‎ 则三棱锥的底面积为；， 而三棱锥的高为；‎ 得： ,故选C 考点：三视图与几何体的体积．‎ ‎4．某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（ ）‎ A． ‎ B． C． D．‎ ‎【答案】D ‎【解析】‎ 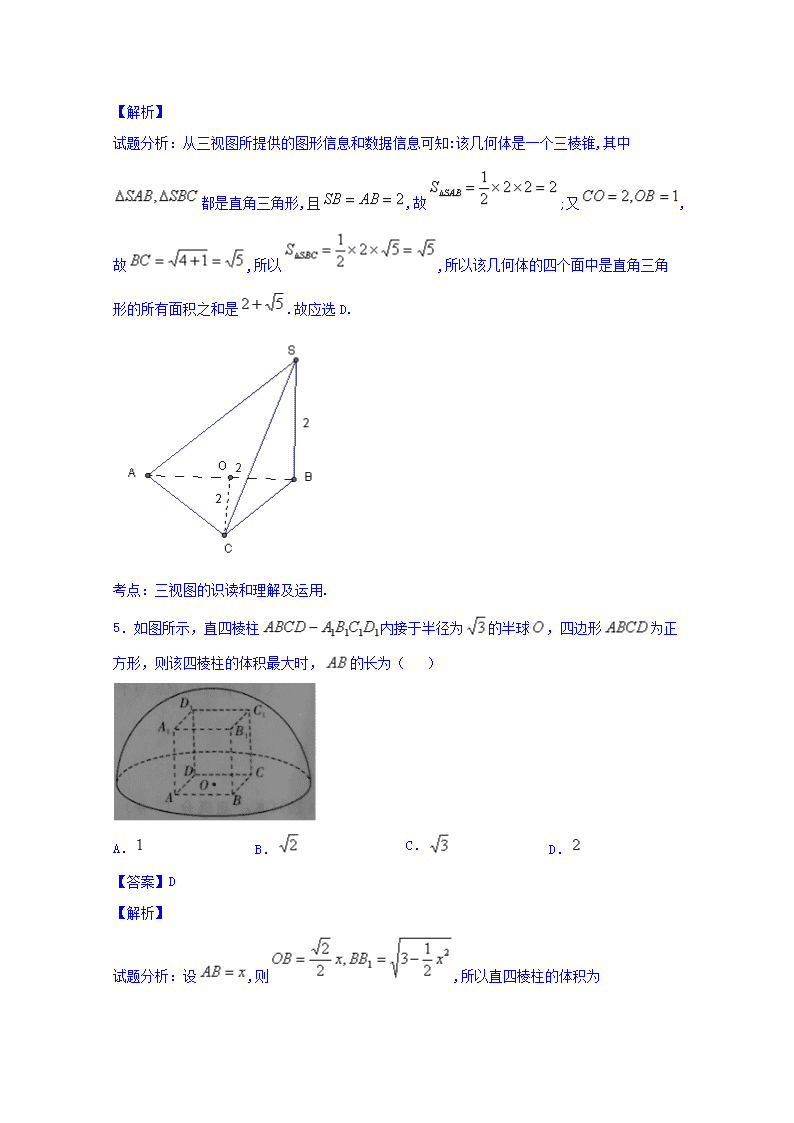试题分析：从三视图所提供的图形信息和数据信息可知:该几何体是一个三棱锥,其中都是直角三角形,且,故;又,故,所以,所以该几何体的四个面中是直角三角形的所有面积之和是.故应选D.‎ 考点：三视图的识读和理解及运用.‎ ‎5．如图所示，直四棱柱内接于半径为的半球，四边形为正方形，则该四棱柱的体积最大时，的长为（ ）‎ A． ‎ B． C． D．‎ ‎【答案】D ‎【解析】‎ 试题分析：设,则,所以直四棱柱的体积为 ‎,令,则,则,故,所以当时,即时,体积最大.故应选D.‎ 考点：导数的知识、四棱柱和球等知识的综合运用.‎ ‎6．某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是（ ）‎ A． ‎ B． C． D．‎ ‎【答案】C ‎【解析】‎ 试题分析：从三视图所提供的图形信息和数据信息可知:该几何体是一个三棱锥如上图,其中都是直角三角形,且,故;又,故,所以,所以该几何体的四个面中是直角三角形的所有面积之和是.故应选C.‎ 考点：三视图的识读和理解及运用.‎ ‎7．如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球半径为（ ）‎ A． ‎ B． C． D．‎ ‎【答案】C ‎ ‎ 考点：三视图的识读和理解及几何体体积的计算.‎ ‎8．已知圆被直线所截得的线段的长度等于2，则等于（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 试题分析：因圆心到直线的距离是,半弦长为,故,解之得,应选B.‎ 考点：直线与圆的位置关系.‎ ‎9．圆与圆的位置关系为（ ）‎ ‎（A）内切 （B）相交 （C）外切 （D）相离 ‎【答案】B ‎【解析】‎ 试题分析：因两圆心距,而,故两圆的位置关系相交,选B.‎ 考点：两圆的位置关系.‎ ‎10．六个面都是平行四边形的四棱柱称为平行六面体．如图甲，在平行四边形ABCD中，有AC2+BD2=2（AB2+AD2），那么在图乙所示的平行六面体ABCD-A1B1C1D1中，等于（ ）‎ A．2（AB2+AD2+） ‎ B．3（AB2+AD2+）‎ C．4（AB2+AD2+） ‎ D．4（AB2+AD2）‎ ‎【答案】C ‎【解析】‎ 试题分析：因在平面上有结论,故由类比推理在空间应有结论,故应选C．‎ 考点：类比推理及运用．‎ ‎11．一直三棱柱的每条棱长都是，且每个顶点都在球的表面上，则球的半径为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 试题分析：球的半径满足 考点：外接球 ‎12．若一个四棱锥底面为正方形, 顶点在底面的射影为正方形的中心, 且该四棱锥的体积为,当其外接球的体积最小时, 它的高为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 试题分析：设四棱锥底面正方形边长为，四棱锥高为，外接球半径为，则，所以，因为，所以时取唯一一个极小值，也是最小值，即外接球的体积最小，因此选A.‎ 考点：导数实际应用 ‎ 第Ⅱ卷（共90分）‎ 二、 填空题（20分，每题5分）‎ 13． 已知矩形的顶点都在半径为的球的球面上，且,棱锥的体积为，则= ________．‎ ‎【答案】4‎ ‎【解析】‎ 试题分析：由题可得四棱锥的侧棱为，则，再由；．‎ 考点：多面体与外接球．‎ 13． 直线与圆相交于两点，若，则的取值范围是______．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：由于圆的半径为2，若，则圆心到直线的距离不大于1，因此 ‎，，答案为.‎ 考点：直线与圆的位置关系..‎ 14． 过点P（1，2）且在Ｘ轴，Ｙ轴上截距相等的直线方程是 .‎ ‎【答案】‎ ‎【解析】‎ 试题分析：当直线过原点时，可设直线的方程为，‎ 代入点P（1，2）可得，故方程为，化为一般式可得；‎ 当直线不过原点时，可设直线的方程为，‎ 代入点P（1，2）可得，故方程为，化为一般式可得；‎ 综上可得所求直线的方程为：.‎ 故答案为：.‎ 考点：直线的截距式方程．‎ 15． 如图，在长方体ABCD—A1B1C1D1中，AB＝3cm，AD＝2cm，AA1＝1cm，则三棱锥B1—ABD1的体积___________cm3.‎ ‎【答案】1‎ ‎【解析】‎ 试题分析：‎ 考点：棱锥体积 二、 解答题（共6小题，共70分）‎ ‎17.(本小题共10分).如图，已知四棱锥中， 平面，底面是直角梯形，且．‎ ‎（1）求证：平面；‎ ‎（2）若是的中点，求三棱锥的体积．‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ 试题分析：（1）证线面垂直可回到判定定理（化为线与两条相交直线垂直来证）．结合条件平面 及所给的边和角的条件可通过解三角形证得，从而证出；另外也可建立空间坐标系，运用向量运算来解决．‎ ‎（2）解：取的中点，连结, 是的中点，∴∥ ‎ 平面，平面 ‎ 即为三棱锥的高， 且 ‎ 由（1）知：，∴，‎ 又，∥，‎ ‎ ,‎ ‎ ‎ 三棱锥的体积为 ‎ ‎【考点】（1）线面垂直的证明；（2）等体积法求几何体的体积．‎ ‎18.(本小题共12分)如图，在三棱锥中，和都是以为斜边的等腰直角三角形.‎ ‎（1）求证：；‎ ‎（2）若，求三棱锥的体积.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）运用线面垂直的性质定理推证；（2）借助题设条件运用三棱锥的体积公式进行求解.‎ 试题解析：‎ ‎（1）证明：取中点，连结.‎ ‎∵和都是以为斜边的等腰直角三角形，∴，，‎ ‎∵，平面，平面，∴平面 ‎∵平面，∴.‎ ‎（2）解：在等腰直角三角形中，， 为斜边的中点，‎ ‎∴，同理得. ‎ ‎∵， ∴是等边三角形.‎ ‎∴.‎ ‎∵平面，‎ ‎∴.‎ 考点：空间的直线与平面的位置关系等有关知识的综合运用．‎ ‎19.(本小题共12分).设有关于的一元二次方程．‎ ‎（Ⅰ）若是从四个数中任取的一个数，是从三个数中任取的一个数，求上述方程有实根的概率；‎ ‎（Ⅱ）若是从区间任取的一个数，是从区间任取的一个数，求上述方程有实根的概率．‎ ‎【答案】（Ⅰ）；（Ⅱ）‎ ‎【解析】‎ 试题分析：设事件为“方程有实根”．‎ 当，时，方程有实根的充要条件为．‎ ‎（Ⅰ）基本事件共12个：‎ ‎．其中第一个数表示的取值，第二个数表示的取值．事件中包含9个基本事件，事件发生的概率为．‎ ‎（Ⅱ）试验的全部结束所构成的区域为．‎ 构成事件的区域为．‎ 所以所求的概率为．‎ 考点：古典概型和几何概型综合 ‎20.(本小题共12分)已知函数.‎ ‎（Ⅰ）求的值域；‎ ‎（Ⅱ）设△的内角A、B、C所对的边分别为a、b、c，已知为锐角，，，，求的值．‎ ‎【答案】（Ⅰ）；（Ⅱ）‎ ‎【解析】‎ 试题分析：（Ⅰ）‎ ‎． ‎ 所以函数的值域是． ‎ ‎（Ⅱ）由，得，‎ 又为锐角，所以，又，，‎ 所以，． ‎ 由，得，又，从而，．‎ 所以，‎ 考点：三角函数变换和正弦定理的应用 ‎21(本小题共12分)已知动点满足方程．‎ ‎（Ⅰ）求动点P到直线距离的最小值；‎ ‎（Ⅱ）设定点，若点之间的最短距离为,求满足条件的实数的取值．‎ ‎【答案】（Ⅰ）；（Ⅱ）或.‎ ‎【解析】‎ 试题分析：‎ ‎（Ⅰ）先点到直线的距离公式建立函数,再用基本不等式求解；（Ⅱ）借助题设条件建立函数关系,再运用二次函数的知识求解.‎ 试题解析：‎ ‎（Ⅰ）‎ 当且仅当时距离取得最小值 ‎（Ⅱ）设点（）, 则 ‎ 设（）,则 ‎ ‎,设（）‎ 对称轴为 ‎ 分两种情况: ‎ ‎（1）时, 在区间上是单调增函数,故时, 取最小值 ‎ ‎∴,∴,∴（舍）‎ ‎（2）＞时,∵在区间上是单调减,在区间上是单调增, ‎ ‎∴时, 取最小值 ‎ ‎∴,∴（舍）‎ 综上所述, 或 ‎ 考点：函数的图象和性质或基本不等式的综合运用．‎ ‎22(本小题共12分).已知数列{an}满足a1＝1，|an＋1－an|＝pn，n∈N*.‎ ‎(1)若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；‎ ‎(2)若p＝，且{a2n－1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式．‎ ‎【答案】(1)；(2)an＝＋·‎ ‎【解析】‎ 试题分析：(1)因为{an}是递增数列，所以an＋1－an＝|an＋1－an|＝pn.而a1＝1，因此.又a1，2a2，3a3成等差数列，所以4a2＝a1＋3a3，因而3p2－p＝0，解得p＝或p＝0.当p＝0时，an＋1＝an，这与{an}是递增数列矛盾，故p＝.‎ ‎(2)由于{a2n－1}是递增数列，因而a2n＋1－a2n－1>0，于是(a2n＋1－a2n)＋(a2n－a2n－1)>0.①‎ 因为<，所以|a2n＋1－a2n|<|a2n－a2n－1|.②‎ 由①②知，a2n－a2n－1>0，因此a2n－a2n－1＝＝.③‎ 因为{a2n}是递减数列，同理可得，a2n＋1－a2n<0，故a2n＋1－a2n＝－＝.④‎ 由③④可知，an＋1－an＝.‎ 于是an＝a1＋(a2－a1)＋(a3－a2)＋…＋(an－an－1)＝1＋－＋…＋ ‎＝1＋·＝＋·.‎ 故数列{an}的通项公式为an＝＋·‎ 考点：数列综合性质综合问题 ‎ ‎ ‎