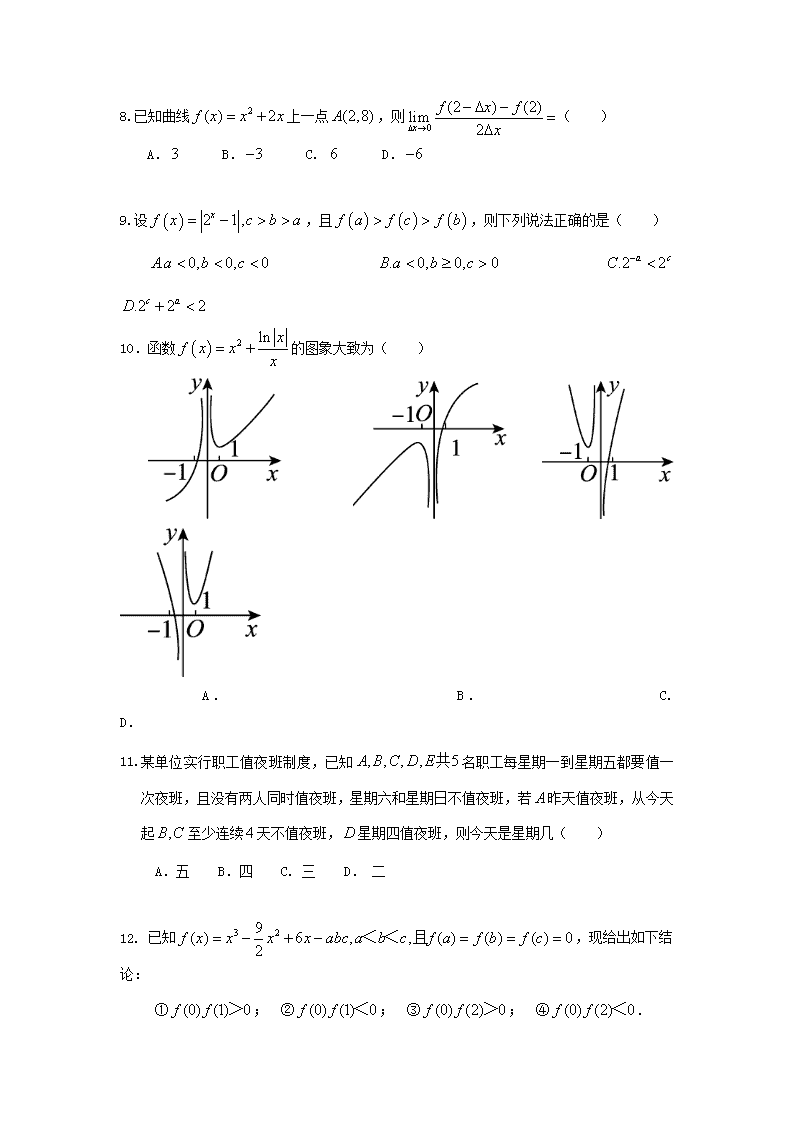2019学年高二数学下学期期末考试试题 文 新人教版-新版 10页

‎2019学年度下学期期末考试 高二 数学（文）试题 第Ⅰ卷(选择题 共60分)‎ 一．选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．若复数满足，则的共轭复数在复平面内对应的点在（ ）‎ A．第一象限 B．第二象限 C.第三象限 D．第四象限 ‎2.设集合，则（ ）‎ A． B． C. D．‎ ‎3．命题“”的否定是（ ）‎ A． B．‎ C. D．‎ ‎4．已知弧度的圆心角所对的弦长为,那么这个圆心角所对的弧长为（ ）‎ A． B． C. D．‎ ‎5．唐代诗人杜牧的七绝唐诗《偶题》传诵至今，“道在人间或可传，小还轻变已多年。今来海上升高望，不到蓬莱不是仙” ，由此推断，后一句中“是仙”是“到蓬莱”的（ ）‎ A．必要条件 B. 充分条件 C.充要条件 D．既非充分又非必要条件 ‎6．若函数的最小值是，则实数的取值范围是（ ）‎ A． B． C. D．‎ ‎7．设角是第二象限角，为其终边上的一点，且，则（ ）‎ A． B． C. D．‎ ‎8.已知曲线上一点，则（ ）‎ A． B． C. D．‎ ‎9.设，且，则下列说法正确的是（ ）‎ ‎ ‎ ‎10．函数的图象大致为（ ）‎ ‎ ‎ A． B． C. D．‎ ‎11.某单位实行职工值夜班制度，已知名职工每星期一到星期五都要值一次夜班，且没有两人同时值夜班，星期六和星期日不值夜班，若昨天值夜班，从今天起至少连续天不值夜班，星期四值夜班，则今天是星期几（ ）‎ A．五 B．四 C. 三 D． 二 ‎12. 已知，现给出如下结论：‎ ‎①； ②； ③； ④.‎ 其中正确结论的序号为（ ）‎ A．②③ B．①④ C.②④ D．①③‎ 第Ⅱ卷(非选择题 共90分)‎ 二．填空题：本题共4小题，每小题5分，共20分.‎ ‎13．已知，则 .‎ ‎14．《聊斋志异》中有这样一首诗：“挑水砍柴不堪苦，请归但求穿墙术。得诀自诩无所阻，额上坟起终不悟.”在这里，我们称形如以下形式的等式具有“穿墙术”： ‎ ‎，，‎ 则按照以上规律，若具有 “穿墙术”，则 .‎ ‎15．若函数的定义域为，值域为，则的取值范围是 ‎ ‎16． 设过曲线上任意一点处的切线为，总存在过曲线上一点处的切线，使得，则实数的取值范围为 .‎ 三．解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.‎ ‎17．(本小题满分10分)‎ 在直角坐标系中以为极点，轴非负半轴为极轴建立极坐标系，圆、直线的极坐标方程分别为.‎ ‎(Ⅰ)求与交点的极坐标；‎ ‎(Ⅱ)设为的圆心， 为与的交点连线的中点，已知直线的参数方程为 ‎，求的值.‎ ‎18．(本小题满分12分)‎ 已知，设：实数满足， ：实数满足．‎ ‎（1）若，且为真，求实数的取值范围；‎ ‎（2）若是的充分不必要条件，求实数的取值范围．‎ ‎19．(本小题满分12分)‎ 已知定义域为的函数是奇函数.‎ ‎（1）求的值；‎ ‎（2）关于的不等式在有解，求实数的取值范围.‎ ‎20．(本小题满分12分)‎ 在直角坐标系中，直线：，在以原点为极点，轴的非负半轴为极轴的极坐标系中，曲线：，若直线与轴正半轴交于点，与曲线交于、两点，其中点在第一象限.‎ ‎（1）求曲线的直角坐标方程及点对应的参数（用表示）；‎ ‎（2）设曲线的左焦点为，若，求直线的倾斜角的值.‎ ‎21．(本小题满分12分)‎ 已知函数.‎ ‎（1）若，求函数的极值；‎ ‎（2）当时，若在区间上的最小值为，求的取值范围.‎ ‎22．(本小题满分12分)‎ 已知函数.‎ ‎（1）若函数不存在单调递减区间，求实数的取值范围；‎ ‎（2）若的两个极值点为，，求的最小值.‎ 大庆实验中学2017-2018学年度下学期期末考试 高二 数学（文） 参考答案 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎— ‎ ‎【解析】（1）由题意知的直角坐标方程为 联立，得，‎ 交点的极坐标为 ‎（2）由（1）得，点与点的坐标分别为，‎ 故直线的直角坐标方程为，‎ 由参数方程可得，，解得 ‎【解析】（1）由得 当时， ，即为真时实数的取值范围是. ‎ 由，得，即为真时实数的取值范围是 ‎ 因为为真，所以真且真，‎ 所以实数的取值范围是. ‎ ‎ （2）由得，‎ 所以， 为真时实数的取值范围是. ‎ 因为 是的充分不必要条件，即是的充分不必要条件 所以且 ‎ 所以实数的取值范围为. ‎ ‎【解析】（1）由为奇函数可知， ，解得.‎ ‎（2）由递增可知在上为减函数，‎ 则关于的不等式，‎ 等价于，即，‎ 因为，所以，‎ 原问题转化为在上有解，‎ ‎∵在区间上为减函数，‎ ‎∴， 的值域为，‎ ‎∴，解得，‎ ‎∴的取值范围是.‎ ‎【解析】‎ ‎（Ⅰ）由得，‎ 即曲线的直角坐标方程为 ‎ 又由题意可知点的横坐标为，代入有 ‎ ‎（2）由（1）知，直线过定点，‎ 将代入，‎ 化简可得 设、对应的参数分别为, ‎ ‎【解析】（1）， ，定义域为，‎ 又 .‎ 当或时；当时 ‎∴函数的极大值为 函数的极小值为.‎ ‎（2）函数的定义域为，‎ 且 ，‎ 令，得或，‎ 当，即时， 在上单调递增，‎ ‎∴在上的最小值是，符合题意；‎ 当时， 在上的最小值是，不符合题意；‎ 当时， 在上单调递减，‎ ‎∴在上的最小值是，不合题意 故的取值范围为 ‎【解析】（1）由函数有意义，则 ‎ 由且不存在单调递减区间，则在上恒成立，‎ ‎ 上恒成立 ‎ ‎ ‎ ‎ ‎ ‎ ‎（2）由知，‎ ‎ 令，即 ‎ 由有两个极值点 ‎ 故为方程的两根，‎ ‎ ，‎ ‎，‎ 则 ‎ ‎ 由 ‎ 由，则上单调递减 ‎，即 ‎ ‎ 由知 综上所述，的最小值为