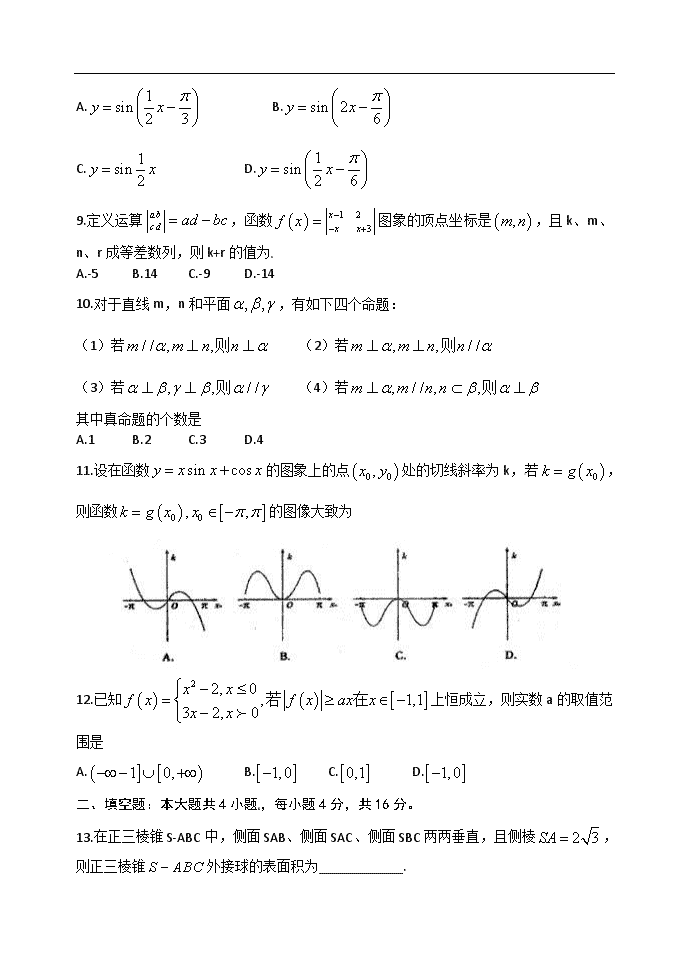山东省莱州一中2013届高三第二次质量检测数学（文）试题 9页

莱州一中 2010 级高三第二次质量检测 数学（文科）试题 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只 有一项是符合要求的. 1.函数    3 lg 2 1 1 xxf x x     的定义域为 A. ,1 B.  0,1 C. 0,1 D. 0, 2.已知点 P tan ,cos  在第三象限，则角 的终边在 A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.一个简单几何体的主视图，左视图如图所示，则其俯视图不可能为 ①长方形；②直角三角形；③圆；④椭圆.其中正确的是 A.① B.② C.③ D.④ 4.三个数 60.7，0.76，log0.76 的大小顺序是 A.0.76＜log0.76＜60.7 B.0.76＜60.7＜log0.76 C.log0.76＜6 0.7＜0.76 D.log0.76＜0.76＜60.7 5.若  1, 2,a b a a b        且 ，则向量 ,a b   的夹角为 A.45° B.60° C.120° D.135° 6.已知 cos2 1 ,052 cos 4 x x       ＜x＜ ，则 tan x 为 A. 4 3  B. 3 4  C.2 D. 2 7.在 ABC 中，解 A、B、C 的对边分别为 a、b、c，若 2 2 2 tan 3a c b B ac   ，则 角 B 的值是 A. 6  B. 3  或 2 3  C. 6  或 5 6  D. 3  8.将函数 sin 3y x      的图象上所有点的横坐标伸长到原来的 2 倍（纵坐标不变），再 将所得图象向左平移 3  个单位，则所得函数图象对应的解析式为 A. 1sin 2 3y x      B. sin 2 6y x      C. 1sin 2y x D. 1sin 2 6y x      9.定义运算 ab c d ad bc  ，函数   1 2 3 x x xf x    图象的顶点坐标是 ,m n ，且 k、m、n、 r 成等差数列，则 k+r 的值为 A.-5 B.14 C.-9 D.-14 10.对于直线 m，n 和平面 , ,   ，有如下四个命题： （1）若 / / , ,m m n n  则 （2）若 , , / /m m n n   则 （3）若 , , / /       则 （4）若 , / / , ,m m n n     则 其中真命题的个数是 A.1 B.2 C.3 D.4 11.设在函数 sin cosy x x x  的图象上的点 0 0,x y 处的切线斜率为 k，若  0k g x ， 则函数    0 0, ,k g x x     的图像大致为 12.已知       2 2, 0 , 1,1 3 2, 0 x xf x f x ax x x x         若 在 上恒成立，则实数 a 的取值范 围是 A.   1 0,    B. 1,0 C. 0,1 D. 1,0 二、填空题：本大题共 4 小题，每小题 4 分，共 16 分。 13.在正三棱锥 S-ABC 中，侧面 SAB、侧面 SAC、侧面 SBC 两两垂直，且侧棱 2 3SA  ， 则正三棱锥 S ABC 外接球的表面积为____________. 14.在等比数列  ,n na a中 ＞0，且 1 2 7 8 4 516,a a a a a a    则 的最小值为________. 15.若实数 x，y 满足 1 2 1 y y x x y m        ，如果目标函数 z x y  的最小值为 2 ，则实数 m=_________。 16.函数    2sinf x x   的图像，其部分图像如图所示， 则  0f  _________. 三、解答题：本大题共 6 小题，共 74 分. 17.（本小题满分 12 分） 在数列 na 中，已知  1 1 1 4 1 1, , 2 3log4 4 n n n n aa b a n Na      . （1）求数列 na 的通项公式； （2）求证：数列 nb 是等差数列； （3）设数列 nc 满足  ,n n n nc a b c  求 的前 n 项和 Sn. 18.（本小题满分 12 分） 已知函数   2 13sin cos cos 2f x x x x   （I）求函数  f x 的对称中心和单调区间； （II ）已知 ABC 内角 A、B、C 的对边分别为 a，b，3，且   1f C  ，若向量    1,sin 2,sinm A n B  与 共线，求 a、b 的值. 19.（本小题满分 12 分） 如图所示，在四棱锥 P—ABCD 中，平面 PAD  平面 ABCD， AB//DC ， △ PA D 是 等 边 三 角 形 ， 已 知 BD=2AD=8 ， 2 4 5AB DC  . （1）设 M 是 PC 上的一点，求证：平面 MBD⊥平面 PAD； （2）求四棱锥 P—ABCD 的体积. 20.（本小题满分 12 分） 各项均为正数的数列 na 中，a1=1，Sn 是数列 na 的前 n 项 和，对任意 n N  ，有  22 2 .n n nS pa pa p p R    （1）求常数 P 的值； （2）求数列 na 的通项公式； （3）记 4 23 nn n Sb n   ，求数列 nb 的前 n 项和 Tn. 21.（本小题满分 12 分） 如图，在多面体 ABC—A1B1C1 中，四边形 ABB1A1 是正方形， AC=AB=1，A1C=A1B，B1C1//BC， 1 1 1 2B C BC . （I）求证：面 1A AC ABC 面 ； （II）求证：AB1//面 A1C1C. 22.（本小题满分 14 分） 已知函数    21 2 1 2ln2f x ax a x x    （a＞0）. （1）若 1 2a  ， 求  f x 在 1, 上的最小值； （2）若 1 2a  ，求函数  f x 的单调区间； （3）当 1 2 ＜a＜1 时，函数  f x 在区间 1,2 上是否有零点，若有，求出零点，若没有， 请说明理由；