- 65.50 KB
- 2021-06-19 发布
第6课时 一次方程及其应用
【课前展练】
1.如果方程是一元一次方程,则 .
2.关于x的方程的解为正实数,则k的取值范围是
3.关于的方程的解是3,则的值为__
4. 某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价.设这种服装的成本价为元,则得到方程( )
A. B. C. D.
5. 在方程3x+4y=16中,当x=3时,y=___;若x、y都是正整数,这个方程的解为_____.
6. 如果是同类项,则、的值是 .
【考点梳理】
考点一:等式及其性质
⑴ 等式:用等号“=”来表示 关系的式子叫等式.
⑵ 性质:① 如果,那么 ;
② 如果,那么 ;如果,那么 .
考点二:方程、一次方程(组)的有关概念
1. ⑴ 方程:含有未知数的 叫做方程;使方程左右两边值相等的 ,叫做方程的解;求方程解的 叫做解方程. 方程的解与解方程不同.
(2) 一元一次方程:只含有 个未知数,并且未知数的次数是 的整式方程叫做一元一次方程;它的一般形式为 .
(3)二元一次方程:含有 未知数(元)并且未知数的次数是 的整式方程. 二元一次方程的解: 适合一个二元一次方程的 未知数的值叫做这个二元一次方程的一个解,一个二元一次方程有 个解.
(4)二元一次方程组:由2个或2个以上的 组成的方程组叫二元一次方程组.
二元一次方程组的解: 使二元一次方程组的 ,叫做二元一次方程组的解.
2. 解一元一次方程的步骤:
①去 ;②去 ;③移 ;④合并 ;⑤系数化为1.
3
3.解二元一次方程的方法步骤:
消元
转化
二元一次方程组 方程.
消元是解二元一次方程组的基本思路,方法有 消元和 消元法两种.
考点三:一次方程(组)的实际应用
会列方程(组)解实际应用题, 熟悉列方程(组)解实际问题的六个步骤(审、设、列、解、验、答), 对不同问题情景, 要熟知其知识构成所涵盖的公式方法:
(1).工程问题:工作量=工作效率×工作时间;
(2) 利息问题:利息=本金×利率×期数, 本息和=本金+利息;
(3) 行程问题:路程=速度×时间, 顺水(风) 速度=静水(风) 速度+水(风)流速度,
逆水(风) 速度=静水(风) 速度-水(风)流速度;
(4) 商品利润率题:商品利润=商品售价-商品进价,商品利润率;
【典型例题】
例1 解方程(1).(2)
例2 关于x的方程的解为非负整数,则正整数的值是?
例3关于x、y的方程组的解是方程3x+2y=34的一组解,那么m的值为多少?
例4.孔明同学在解方程组的过程中,错把
3
看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线过点(3,1),则的正确值应该是 .
–2
3
4
(备用图)
2y–x
–2
3
4
x
y
(第5题)
a
b
c
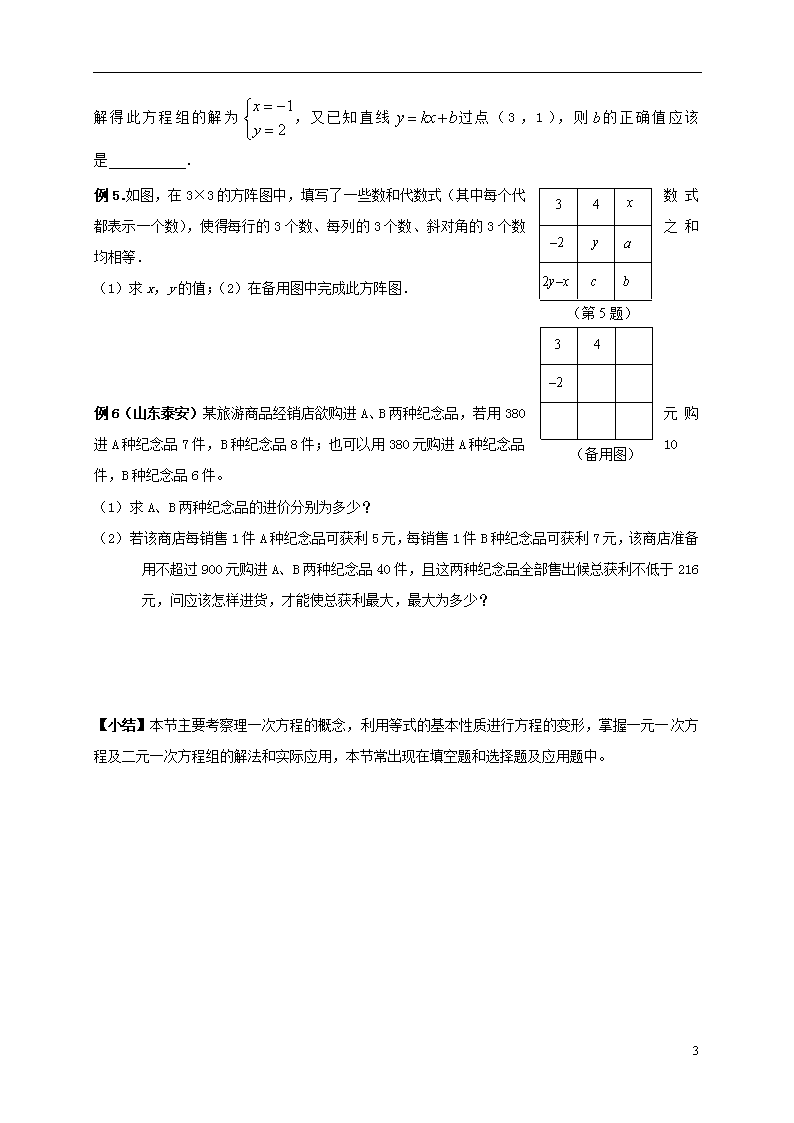
例5.如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.
(1)求x,y的值;(2)在备用图中完成此方阵图.
例6(山东泰安)某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件。
(1) 求A、B两种纪念品的进价分别为多少?
(2) 若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出候总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
【小结】本节主要考察理一次方程的概念,利用等式的基本性质进行方程的变形,掌握一元一次方程及二元一次方程组的解法和实际应用,本节常出现在填空题和选择题及应用题中。
3
相关文档
- 2018年江苏省无锡市中考数学试题含2021-06-19 22:53:0112页
- 2019四川省广安市中考数学试题(解析2021-06-19 21:30:3125页
- 2019广东省深圳中考数学试题(word版2021-06-19 20:45:0112页
- 淄博市2020年中考数学试题及答案2021-06-19 19:33:5421页
- 2018年四川省凉山州中考数学试题(扫2021-06-19 19:26:0211页
- 2019江苏省苏州市中考数学试题(解析2021-06-19 19:20:0321页
- 2013年山东省日照市中考数学试题(含2021-06-19 18:02:5012页
- 济宁中考数学试题答案2021-06-19 17:21:0319页
- 精选20XX吉林中考数学 [吉林省20XX2021-06-19 15:38:228页
- 四川省成都市2017年中考数学试题2021-06-19 15:34:2127页