数学理卷·2018届江西省赣州市寻乌中学高三上学期期中考试（2017 11页

江西省寻乌中学2017届上学期高三期中考试试卷 数学（理工类）试卷 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.的值为（ ）‎ A． B． C． D．‎ ‎2.已知向量，，若，则实数的值为（ ）‎ A． B． C． D． ‎ ‎3.已知向量，，，则（ ）‎ A． B． C． D． ‎ ‎4.已知，则的值为（ ）‎ A． B． C． D． ‎ ‎5.《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一，书中有这样的一道题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的是较小的两分之和，则最小的1份为（ ）‎ A． B． C． D． ‎ ‎6.等比数列中，，则“”是“”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎ ‎7.已知函数（，）的图象如图所示，它与轴相切于原点，且轴与函数图象所围成区域（图中阴影部分）的面积为，则的值为（ ）‎ A． B． C． D． ‎ ‎8.已知函数是定义域为的偶函数，且，若在上是减函数，记，，，则（ ）‎ A． B． C． D． ‎ ‎9.将函数的图象向右平移个单位后得到函数的图象，若函数在区间和上均单调递增，则实数的取值范围是（ ）‎ A． B． C． D． ‎ ‎10.已知数列满足（），，且，若为数列的前项和，则的最小值为（ ）‎ A． B． C． D． ‎ ‎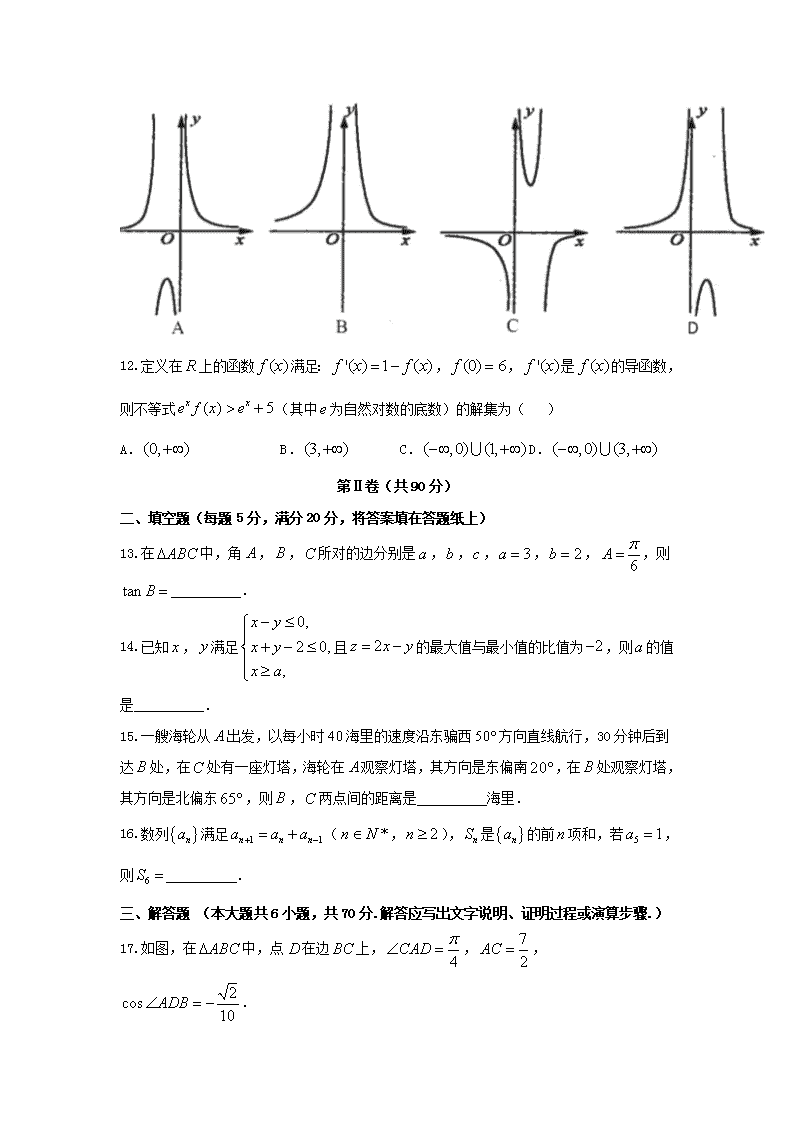11.已知函数（其中为自然对数的底数），则的大致图象为（ ）‎ ‎12.定义在上的函数满足：，，是的导函数，则不等式（其中为自然对数的底数）的解集为（ ）‎ A． B． C．D． ‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.在中，角，，所对的边分别是，，，，，，则 ．‎ ‎14.已知，满足且的最大值与最小值的比值为，则的值是 ．‎ ‎15.一艘海轮从出发，以每小时海里的速度沿东骗西方向直线航行，30分钟后到达处，在处有一座灯塔，海轮在观察灯塔，其方向是东偏南，在处观察灯塔，其方向是北偏东，则，两点间的距离是 海里．‎ ‎16.数列满足（，），是的前项和，若，则 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.如图，在中，点在边上，，，．‎ ‎（1）求的值；‎ ‎（2）若的面积为7，求的长．‎ ‎18.已知数列的前项和为，，（）．‎ ‎（1）求数列的通项公式；‎ ‎（2）设（），数列的前项和为，证明：（）．‎ ‎19.在中，内角，，所对边长分别为，，，，，．‎ ‎（1）求的最大值；‎ ‎（2）求函数的值域．‎ ‎20.已知数列是公差为正数的等差数列，其前项和为，且，．‎ ‎（1）求数列的通项公式；‎ ‎（2）数列满足，．　‎ ‎①求数列的通项公式；②是否存在正整数，（），使得，，成等差数列？若存在，求出，的值；若不存在，请说明理由.‎ ‎21.已知为常数，，函数，（其中是自然对数的底数）.‎ ‎（1）过坐标原点作曲线的切线，设切点为，求证：；‎ ‎（2）令，若函数在区间上是单调函数，求的取值范围．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 在极坐标系中，圆的极坐标方程为：．若以极点为原点，极轴所在直线为轴建立平面直角坐标系．‎ ‎（1）求圆的参数方程；‎ ‎（2）在直角坐标系中，点是圆上动点，试求的最大值，并求出此时点的直角坐标．‎ ‎23.选修4-5：不等式选讲 已知，都是实数，，．‎ ‎（1）若，求实数的取值范围；‎ ‎（2）若对满足条件的所有，都成立，求实数的取值范围．‎ 江西省寻乌中学2017届上学期高三期中考试试卷数学（理工类）试卷答案 一、选择题 ‎1-5: 6-10: 11、12：‎ 二、填空题 ‎13. 14. 15. 16.‎ 三、解答题 ‎17.解：（1）因为，所以，‎ 又因为，所，‎ 所以．‎ ‎（2）在中，由正弦定理，‎ 故．‎ 又，解得．‎ 在中，由余弦定理得 ‎．　‎ ‎18.解：（1）当时，，解得；‎ 当时，，，‎ 以上两式相减，得，∴，‎ ‎∴，‎ ‎∴‎ ‎（2）‎ 当时，；‎ 当时，，‎ ‎∴，‎ ‎∴（）．‎ ‎19.解：（1），，即，‎ 又，所以，即的最大值为16，‎ 当且仅当，时取得最大值．‎ ‎（2）结合（1）得，，所以，‎ 又，所以，‎ ‎，‎ 因为，所以，‎ 当，即时，，‎ 当，即时，，‎ 所以，函数的值域为．‎ ‎20.解：（1）设数列的公差为，则．‎ 由，，得解得或（舍去）．‎ 所以．‎ ‎（2）①因为，，‎ 所以，‎ ‎，‎ 即，，…，，（）‎ 累加得，‎ 所以，‎ 也符合上式，‎ 故，．‎ ‎②假设存在正整数、（），使得，，成等差数列，则．‎ 又，，，‎ 所以，即，‎ 化简得：，‎ 当，即时，（舍去）；‎ 当，即时，符合题意．‎ 所以存在正整数，，使得，，成等差数列．‎ ‎21.解：（1）（），‎ 所以切线的斜率，‎ 整理得，显然，是这个方程的解，‎ 又因为在上是增函数，‎ 所以方程有唯一实数解，‎ 故．‎ ‎（2），，‎ 设，则，‎ 易知在上是减函数，从而．‎ ‎①当，即时，，在区间上是增函数，‎ ‎∵，∴在上恒成立，即在上恒成立．‎ ‎∴在区间上是减函数，‎ 所以满足题意．　‎ ‎②当，即时，设函数的唯一零点为，‎ 则在上递增，在上递减，‎ 又∵，∴，‎ 又∵，‎ ‎∴在内有唯一一个零点，‎ 当时，，当时，.‎ 从而在递减，在递增，与在区间上是单调函数矛盾.‎ ‎∴不合题意．‎ 综上①②得，．‎ ‎22.解：（1）因为，所以，‎ 即为圆的普通方程，‎ 所以所求的圆的参数方程为（为参数）．‎ ‎（2）由（1）可得，设点，‎ ‎，‎ 设，则，所以，‎ 当时，，此时，，即，，‎ 所以，，点的直角坐标为时．‎ ‎23.解：（1）‎ 由得或 解得或，‎ 故所求实数的取值范围为．‎ ‎（2）由且，得，‎ 又∵，‎ ‎∴，‎ ‎∵的解集为，‎ ‎∴的解集为，‎ ‎∴所求实数的取值范围为．‎