- 1.06 MB
- 2021-06-19 发布
铜仁一中2017-2018学年高三第一次月考
文 科 数 学 试 卷
一、选择题(每小题5分,共60分)
(1)、设全集U={x∈N|x<6},集合A={1,3},B={3,5},则∁U(A∪B)等于( )
A.{1,4} B.{1,5}
C.{2,5} D.{2,4}
(2、设z=1-i (i是虚数单位),则+等于
A.2-2i B.2+2i C.3-i D.3+i
(3)、命题“∀n∈N,f(n)∈N且f(n)≤n”的否定形式是( )
A.∀n∈N,f(n)∉N且f(n)>n
B.∀n∈N,f(n)∉N或f(n)>n
C.∃n0∈N,f(n0)∉N且f(n0)>n0
D.∃n0∈N,f(n0)∉N或f(n0)>n0
(4)、已知sin(π-α)=,且α∈(-,0),则tan(2π-α)的值为( )
A.- B.
C.± D.
(5)、设θ是第三象限角,且=-cos ,则是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
(6)、设D为△ABC所在平面内一点,=3,则( )
A. =-+ B.=-
C.=+ D.=-
(7)、设函数f(x)=若f(a)<1,则实数a的取值范围是( )
A.(-∞,-3) B.(1,+∞)
C.(-3,1) D.(-∞,-3)∪(1,+∞)
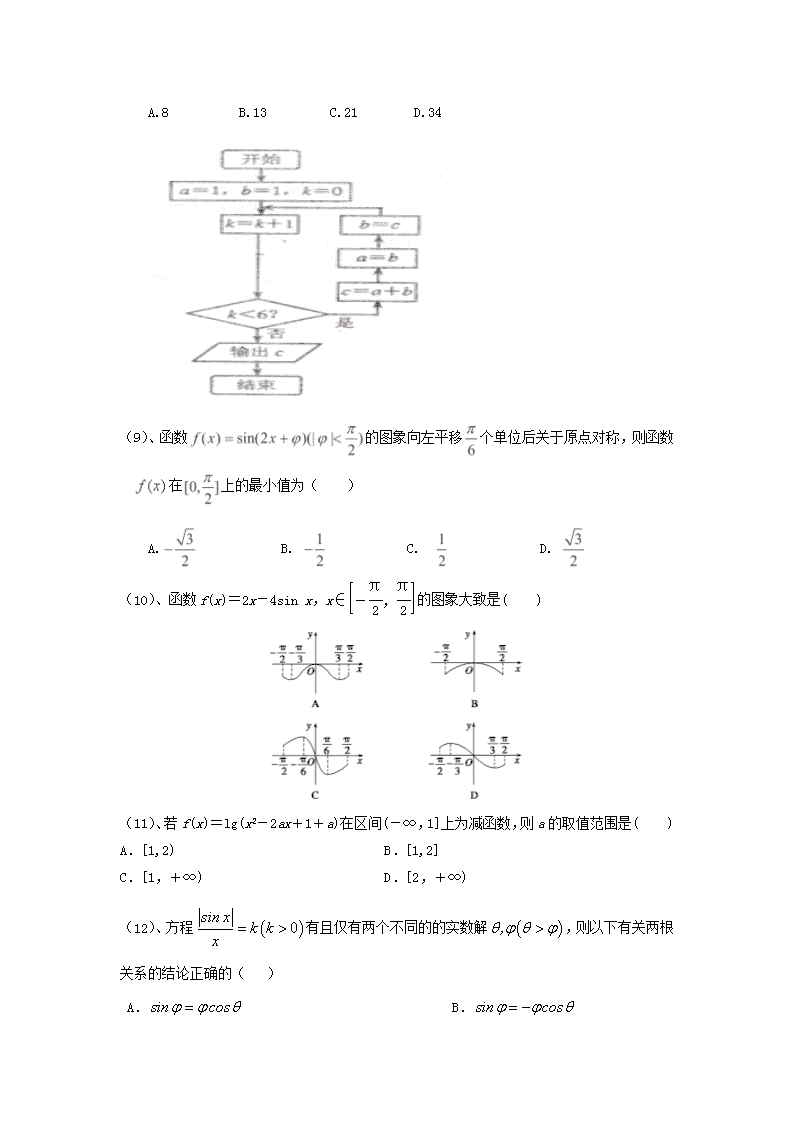
(8)、执行如图所示的程序框图,则输出的c的值是
A.8 B.13 C.21 D.34
(9)、函数的图象向左平移个单位后关于原点对称,则函数在上的最小值为( )
A. B. C. D.
(10)、函数f(x)=2x-4sin x,x∈的图象大致是( )
(11)、若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上为减函数,则a的取值范围是( )
A.[1,2) B.[1,2]
C.[1,+∞) D.[2,+∞)
(12)、方程有且仅有两个不同的的实数解,则以下有关两根关系的结论正确的( )
A. B.
C. D.
二、填空题(每小题5分,共20分)
(13)、设曲线y=ex在点(0,1)处的切线与曲线y=(x>0)上点P处的切线垂直,则P的坐标为________.
(14)、已知2tan α·sin α=3,-<α<0,则sin α等于________.
(15)、已知a与b是两个不共线向量,且向量a+λb与-(b-3a)共线,则λ=________.
(16)、已知函数f(x)=-x2+4x-3ln x在区间[t,t+1]上不单调,则t的取值范围是________.
三、解答题
(17)、(本题满分12分)
候鸟每年都要随季节的变化而进行大规模的迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为 (其中a、b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(1)求出a、b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要多少个单位?
(18)、(本题满分12分)
如图,函数
的图象与轴交于点,且该函数相邻两零点
距离为.
(Ⅰ)求和的值;
(Ⅱ)若,
求的值
(19)、(本题满分12分)
已知命题p:||≤ 2;命题。若是的必要而不充分条件,求实数的取值范围。
(20) 、(本题满分12分)
在中,角所对的边分别是,已知.
(Ⅰ)若的面积等于,求;
(Ⅱ)若,求的面积.
(21) 、(本题满分12分)
已知函数 , .
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求函数的单调区间;
(Ⅲ)当时,函数在上的最大值为,若存在,使得成立,求实数b的取值范围.
三、选做题
(22)、(本小题满分10分)选修4-4;
在直角坐标平面内,直线过点,且倾斜角,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知圆C的极坐标方程为。
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设直线与圆C交于A,B两点,求的值
(23)、(本小题满分10分)选修4-5:不等式选讲
设函数,其中。
(Ⅰ)当时,求不等式的解集;(Ⅱ)若不等式的解集为 ,求a的值。
铜仁一中2018届高三第一次月考
文科数学参考答案
一、选择题
DBDBB ACBAD AB
二、填空题
13、 (1,1) 14、 - 15、-
16、(0,1)∪(2,3)
解析 由题意知f′(x)=-x+4-
=-,
由f′(x)=0得函数f(x)的两个极值点为1和3,
则只要这两个极值点有一个在区间(t,t+1)内,
函数f(x)在区间[t,t+1]上就不单调,
由t<1