- 2.77 MB
- 2021-06-19 发布
探索图形
用棱长
1
cm
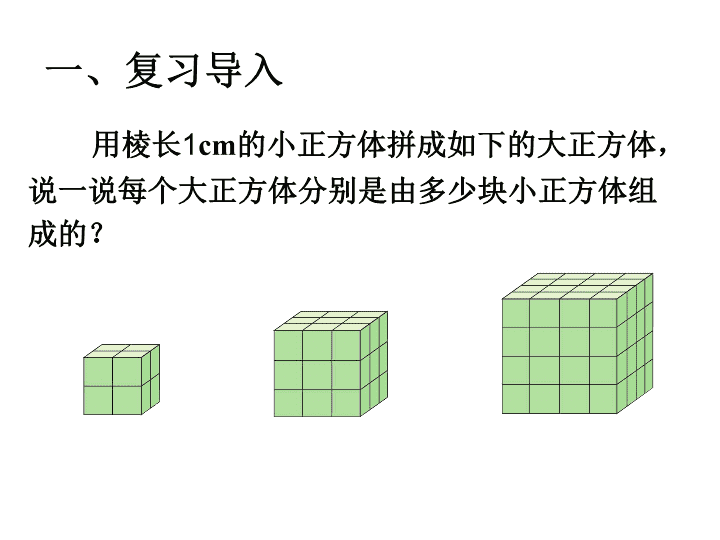
的小正方体拼成如下的大正方体,
说一说每个大正方体分别是由多少块小正方体组
成的?
一、复习导入
用棱长
1
cm
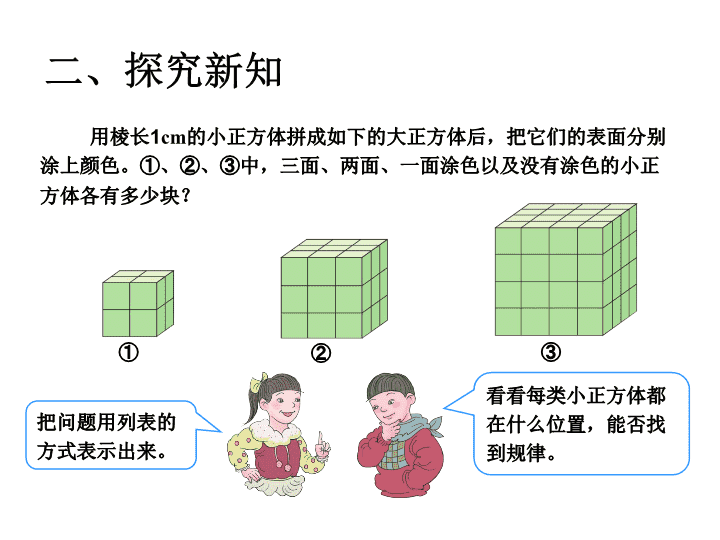
的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。
①
、
②
、
③
中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
二、探究新知
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
用棱长
1
cm
的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。
①
、
②
、
③
中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
8
0
0
0
8
12
6
1
8
24
24
8
8
36
54
27
8
48
96
64
按这样的规律摆下去,第
④
、
⑤
个正方体的结果会
是怎样的呢?
二、探究新知
①
②
③
①
②
③
④
⑤
二、探究新知
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
8
0
0
0
8
12
6
1
8
24
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
观察上表,你能发现什么?
在顶点位置的正方体露出
3
个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是
8
个。
二、探究新知
观察上表,你能发现什么?
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
8
0
0
0
8
12
6
1
8
24
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
在每条棱中间位置的正方体露出
2
个面,两面涂色的块数与棱有关,即
(
n
-
2
)
×
12
。
二、探究新知
观察上表,你能发现什么?
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
8
0
0
0
8
12
6
1
8
24
24
8
8
36
54
27
8
48
96
64
①
②
③
④
⑤
在每个面中间位置的正方体露出
1
个面,一面涂色的块数与面有关,即
(
n
-
2
)
×
(
n
-
2
)
×
6
。
你能继续写出第
⑥
、
⑦
、
⑧
个大正方体中
4
类小正方体的块数吗?
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
8
0
0
0
8
12
6
1
8
24
24
8
8
36
54
27
8
48
96
64
8
60
150
125
8
72
216
216
8
84
294
343
三、知识运用
①
②
③
④
⑤
⑥
⑦
⑧
四、布置作业
如果摆成下面的几何体,你会数吗?
4
10
20
相关文档
- 人教版5年级下数学教学课件:4_9约分2021-06-04 23:24:2312页
- 人教版5年级下数学教学课件:3的倍数2021-06-02 11:08:3413页
- 人教版5年级下数学教学课件:折线统2021-05-29 01:57:2510页
- 人教版5年级下数学教学课件:4_7最大2021-05-12 16:36:0912页
- 人教版5年级下数学教学课件:4_12通2021-05-08 16:44:2413页
- 人教版5年级下数学教学课件:4_2分数2021-05-08 16:16:2711页
- 人教版5年级下数学教学课件:2、5的2021-05-07 15:20:1213页
- 人教版5年级下数学教学课件:1_1观察2021-05-07 14:54:3411页
- 人教版5年级下数学教学课件:6_4分数2021-05-06 09:45:058页
- 人教版5年级下数学教学课件:3_5体积2021-04-21 21:23:4915页