- 200.00 KB
- 2021-06-19 发布
第二十二章 22.1.2二次函数y=ax2的图象和性质
知识点1:二次函数y=ax2图象的画法
二次函数y=ax2的图象的画法:
(1)列表:先取原点(0,0),然后在原点的两边,对称地选取几个x值,求出函数值列表.
(2)描点:在平面直角坐标系中描出表中数据对应的各点,一般先描y轴一侧的几个点,然后由对称性描出另一侧的几个点.
(3)连线:用平滑的曲线顺次连接各点,就得到了二次函数y=ax2的图象.
知识点2:二次函数y=ax2的性质
1.二次函数y=ax2的图象是一条抛物线.
2.抛物线y=ax2的对称轴是y轴,顶点是原点.a>0时,抛物线开口向上,顶点是抛物线的最低点;a<0时,抛物线开口向下,顶点是抛物线的最高点.
3.抛物线y=ax2的开口大小是由|a|决定的,|a|越大,开口越小;|a|越小,开口越大.
4.具体性质如下表所示:
函数
图象
开口方向
顶点坐标
对称轴
增减性
最大(小)值
y=ax2
a>0
向上
(0,0)
y轴
x>0时,y随x增大而增大;
x<0时,y随x增大而减小
当x=0时,
y最小值=0
a<0
向下
(0,0)
y轴
x>0时,y随x增大而减小;
x<0时,y随x增大而增大
当x=0时,y最大值=0
3
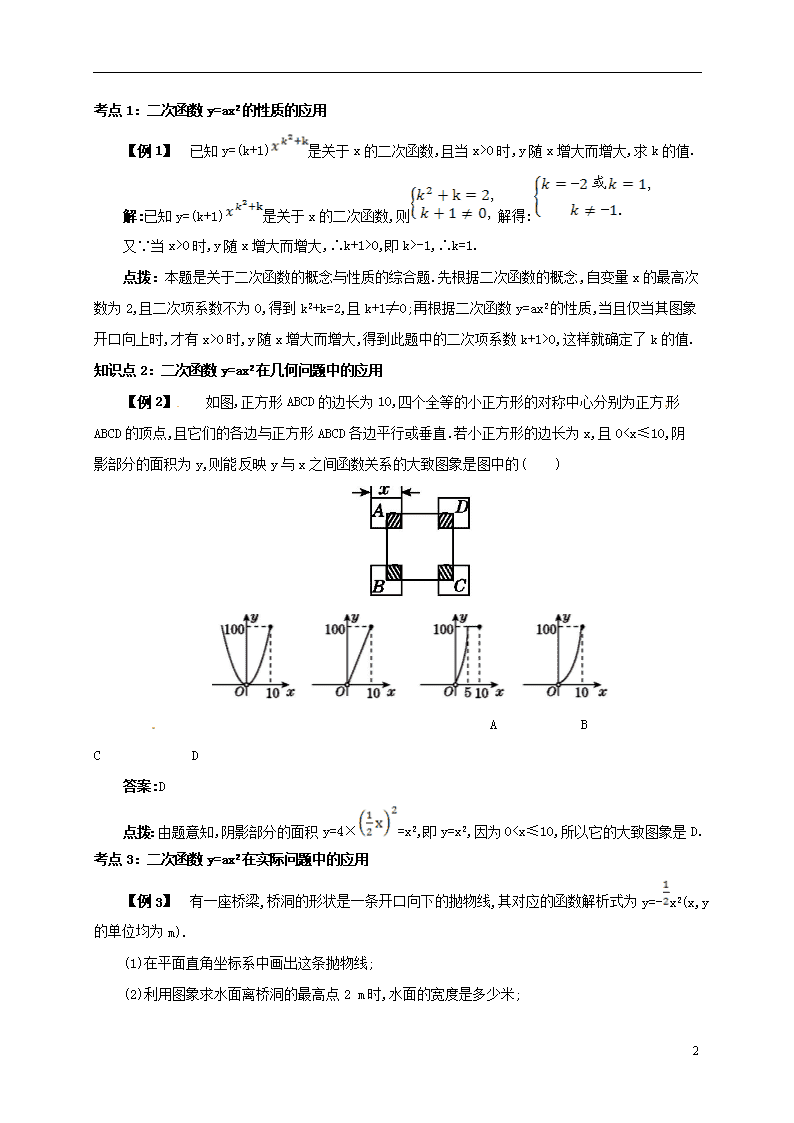
考点1:二次函数y=ax2的性质的应用
【例1】 已知y=(k+1)是关于x的二次函数,且当x>0时,y随x增大而增大,求k的值.
解:已知y=(k+1)是关于x的二次函数,则解得:
又∵当x>0时,y随x增大而增大,∴k+1>0,即k>-1,∴k=1.
点拨:本题是关于二次函数的概念与性质的综合题.先根据二次函数的概念,自变量x的最高次数为2,且二次项系数不为0,得到k2+k=2,且k+1≠0;再根据二次函数y=ax2的性质,当且仅当其图象开口向上时,才有x>0时,y随x增大而增大,得到此题中的二次项系数k+1>0,这样就确定了k的值.
知识点2:二次函数y=ax2在几何问题中的应用
【例2】 如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别为正方形ABCD的顶点,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0
相关文档
- 九年级上册数学周周测第二十二章 2021-06-18 01:07:335页
- 2020中考数学试题分类汇编 考点16 2021-06-17 23:17:1342页
- 2021高考数学新高考版一轮习题:专题2021-06-17 22:55:025页
- 2020九年级数学上册二次函数的性质2021-06-17 22:10:316页
- 中考数学试题分类汇编二次函数2021-06-17 21:51:1393页
- 2020九年级数学下册 二次函数的图2021-06-17 20:22:304页
- 2019届中考数学一轮复习 第39课时 2021-06-17 19:00:494页
- 北师大版九年级下册数学同步练习2-2021-06-17 18:52:412页
- 2020九年级数学下册 第二章 二次2021-06-17 18:10:325页
- 2019九年级数学上册 第二十二章 222021-06-17 12:52:174页