2020年高考数学(理)二轮复习讲练测 专题13 算法、推理与证明、复数（练）（原卷版） 4页

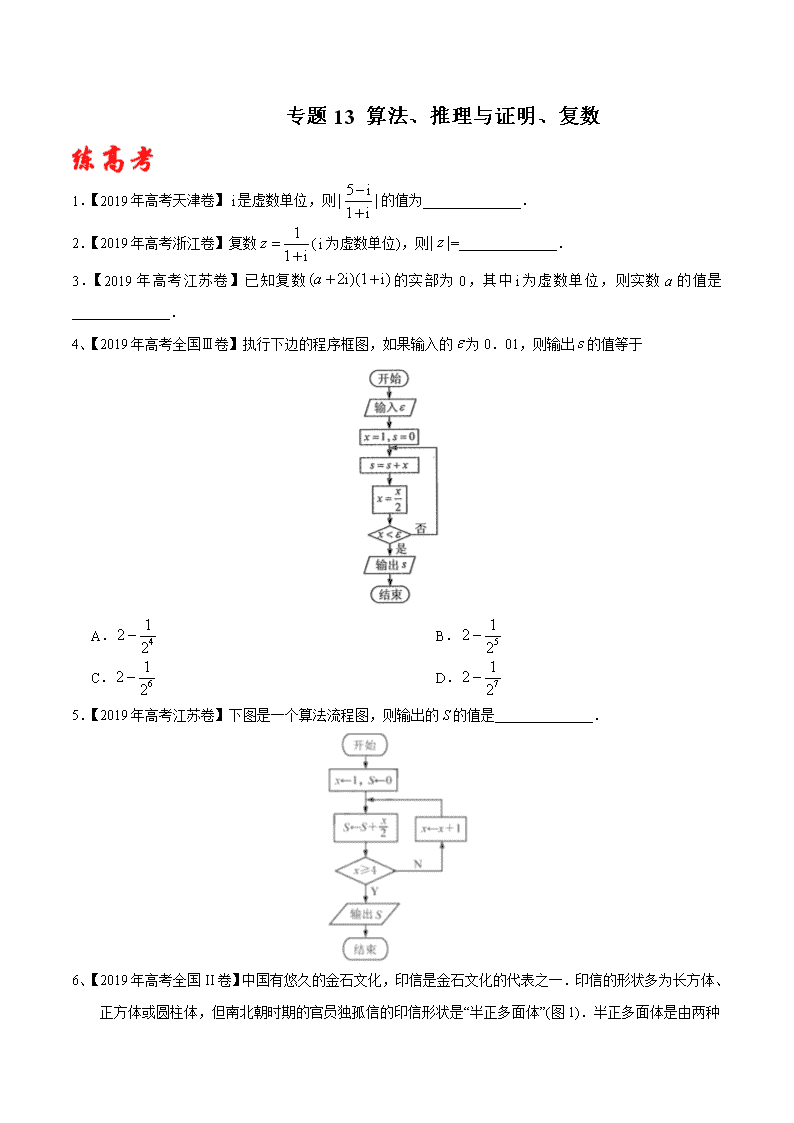
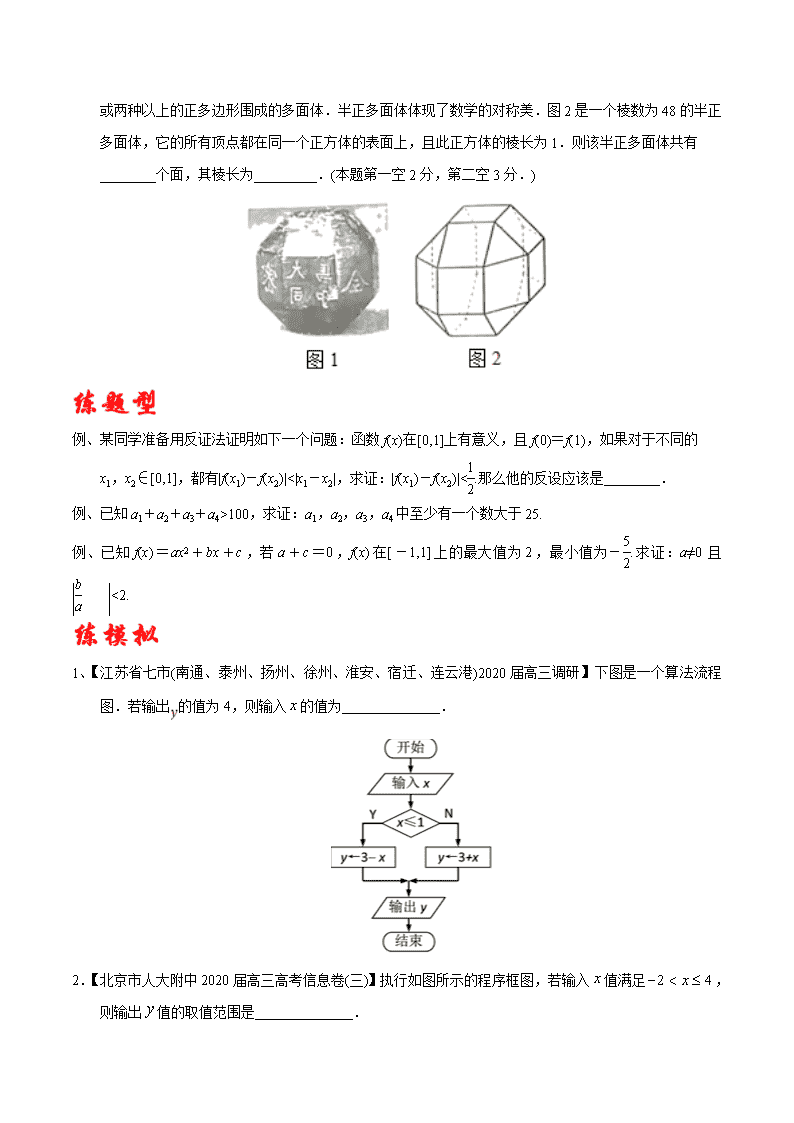
专题13 算法、推理与证明、复数 ‎1．【2019年高考天津卷】是虚数单位，则的值为______________．‎ ‎2．【2019年高考浙江卷】复数(为虚数单位)，则=______________．‎ ‎3．【2019年高考江苏卷】已知复数的实部为0，其中为虚数单位，则实数a的值是______________．‎ ‎4、【2019年高考全国Ⅲ卷】执行下边的程序框图，如果输入的为0．01，则输出的值等于 A． B．‎ C． D．‎ ‎5．【2019年高考江苏卷】下图是一个算法流程图，则输出的S的值是______________．‎ ‎6、【2019年高考全国II卷】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1)‎ ‎．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．(本题第一空2分，第二空3分．)‎ 例、某同学准备用反证法证明如下一个问题：函数f(x)在[0,1]上有意义，且f(0)＝f(1)，如果对于不同的 x1，x2∈[0,1]，都有|f(x1)－f(x2)|<|x1－x2|，求证：|f(x1)－f(x2)|<.那么他的反设应该是________．‎ 例、已知a1＋a2＋a3＋a4>100，求证：a1，a2，a3，a4中至少有一个数大于25.‎ 例、已知f(x)＝ax2＋bx＋c，若a＋c＝0，f(x)在[－1,1]上的最大值为2，最小值为－.求证：a≠0且<2.‎ ‎1、【江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2020届高三调研】下图是一个算法流程图．若输出的值为4，则输入的值为______________．‎ ‎2．【北京市人大附中2020届高三高考信息卷(三)】执行如图所示的程序框图，若输入值满足，则输出值的取值范围是______________．‎ ‎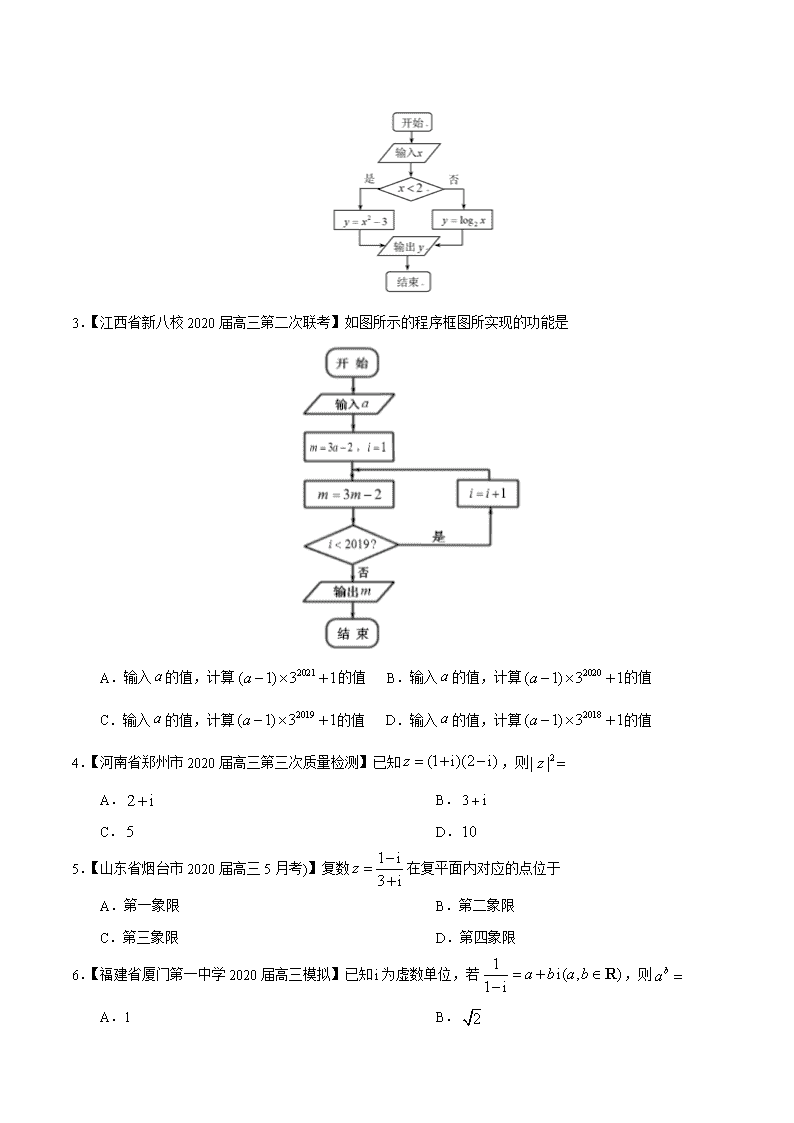3．【江西省新八校2020届高三第二次联考】如图所示的程序框图所实现的功能是 A．输入的值，计算的值 B．输入的值，计算的值 C．输入的值，计算的值 D．输入的值，计算的值 ‎4．【河南省郑州市2020届高三第三次质量检测】已知，则 A． B．‎ C． D．‎ ‎5．【山东省烟台市2020届高三5月考)】复数在复平面内对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎6．【福建省厦门第一中学2020届高三模拟】已知为虚数单位，若，则 A．1 B．‎ C． D．2‎ ‎7．【四川省宜宾市2020届高三诊断】欧拉公式：为虚数单位)，由瑞士数学家欧拉发明，它建立了三角函数与指数函数的关系，根据欧拉公式，‎ A．1 B．‎ C． D．‎ ‎8．(2020·宁波模拟)分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证0　　　　　 　　　 B．a－c>0‎ C．(a－b)(a－c)>0 D．(a－b)(a－c)<0‎ ‎9．【陕西省延安市2020届高考模拟试题数学】甲、乙、丙三位教师分别在延安、咸阳、宝鸡的三所中学里教不同的学科，已知：‎ ‎①甲不在延安工作，乙不在咸阳工作；‎ ‎②在延安工作的教师不教学科；‎ ‎③在咸阳工作的教师教学科；‎ ‎④乙不教学科.‎ 可以判断乙工作的地方和教的学科分别是______、_____．‎ ‎10．观察下列式子：1,1＋2＋1,1＋2＋3＋2＋1,1＋2＋3＋4＋3＋2＋1，…，由以上可推测出一个一般性结论：对于n∈N*,1＋2＋…＋n＋…＋2＋1＝________.‎