专题11+函数++指数函数-2019年高考数学（理）高频考点名师揭秘与仿真测试 9页

‎2019年高考数学（理）高频考点名师揭秘与仿真测试　‎ ‎11 函数 指数函数 ‎ 【考点讲解】‎ 一、 具本目标：指数函数 ‎（1）了解指数函数模型的实际背景.‎ ‎（2） 理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算.‎ ‎（3） 理解指数函数的概念及其单调性，掌握指数函数图像通过的特殊点，会画底数为2，3，10，1/2，1/3的指数函数的图像．‎ ‎（4） 体会指数函数是一类重要的函数模型.‎ 二、知识概述：‎ 根式和分数指数幂 ‎1.根式 ‎(1)概念：式子 叫做根式，其中n叫做根指数，a叫做被开方数.‎ ‎(2)性质：()n＝a(a使有意义)；当n为奇数时，＝a，当n为偶数时，＝|a|＝ ‎2.分数指数幂 ‎ (1)规定：正数的正分数指数幂的意义是a＝(a>0，m，n∈N*，且n>1)；‎ 正数的负分数指数幂的意义是a－＝(a>0，m，n∈N*，且n>1)；‎ ‎0的正分数指数幂等于0；‎ ‎0的负分数指数幂没有意义. 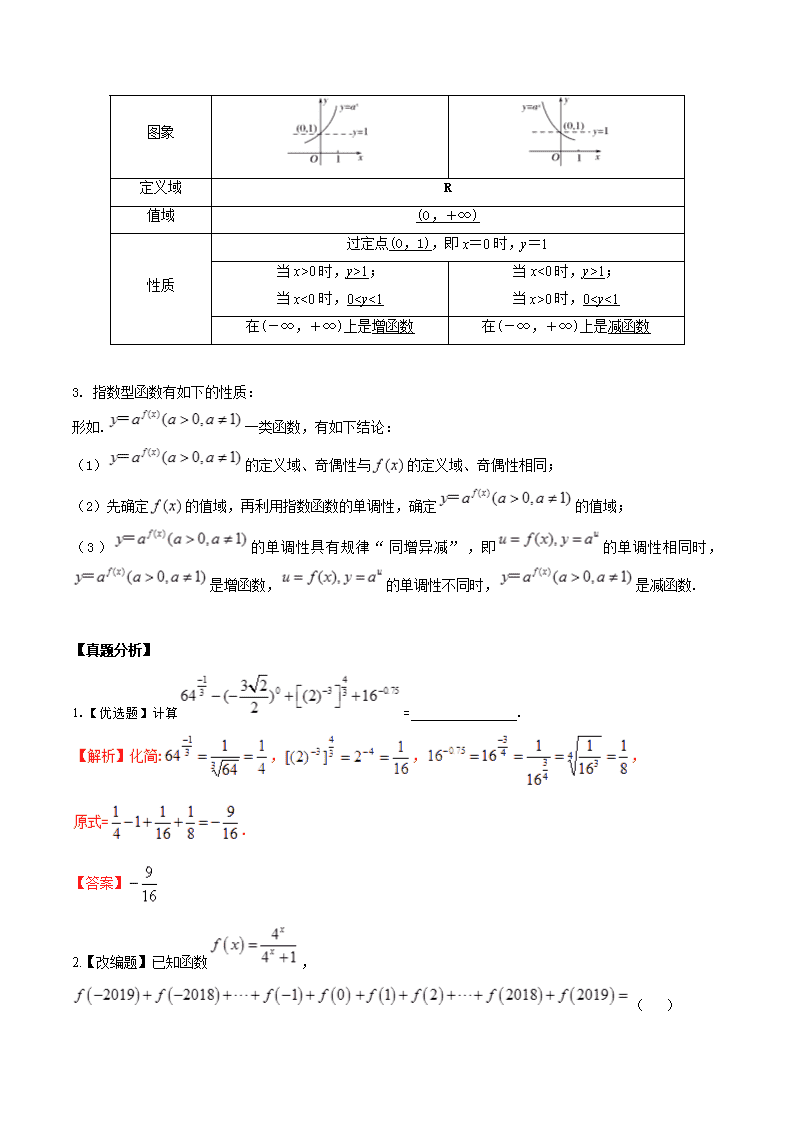‎ ‎(2)有理指数幂的运算性质(注意逆用)‎ ‎(1) (2) ‎ ‎ (3)．(4) ‎ ‎2.指数函数及其性质 ‎(1)概念：函数y＝ax(a>0且a≠1)叫做指数函数，其中指数x是变量，函数的定义域是R，a是底数.‎ ‎(2)指数函数的图象与性质：‎ a>1‎ ‎00时，y>1；‎ 当x<0时，01；‎ 当x>0时，0b>1.若logab+logba=，ab=ba，则a= ，b= .‎ ‎【解析】本题考点是指对数的运算，设，因为，‎ 因此 ‎【答案】 ‎ ‎【易错提示】在解方程时，要注意，若没注意到，方程的根有两个，由于增根导致错误．‎ ‎9.【2016高考江苏卷】已知函数.‎ 设.（1）求方程的根；‎ ‎（2）若对任意,不等式恒成立，求实数的最大值；‎ ‎（3）若，函数有且只有1个零点，求的值。‎ ‎【分析】本题考点是指数函数、基本不等式、利用导数研究函数单调性及零点 ‎（1）①根据指数间倒数关系转化为一元二次方程，求方程根.‎ ‎②根据指数间平方关系，将不等式转化为一元不等式，再利用变量分离转化为对应函数最值，即的最小值，最后根据基本不等式求最值 （2） 先分析导函数零点情况：唯一零点，再确定原函数单调变化趋势：先减后增，从而结合图像确定唯 一零点必在极值点取得，而，因此极值点必等于零，进而求出的 值.本题难点在证明，这可利用反证法：若，则可寻找出一个区间，由结合零点存在定理可得函数存在另一零点，与题意矛盾，其中可取；若，同理可得.‎ 因为对于恒成立，且，所以对于恒成立.‎ 而，且，‎ 所以，故实数的最大值为4.‎ ‎（2）因为函数只有1个零点，而，‎ 所以0是函数的唯一零点.‎ 因为，又由知，‎ 所以有唯一解.‎ 令，则，‎ 从而对任意，，所以是上的单调增函数，‎ 于是当，；当时，.‎ 因而函数在上是单调减函数，在上是单调增函数.‎ 下证.‎ 若，则，于是，‎ 又，且函数在以和为端点的闭区间上的图象不间断，所以在和之间存在的零点，记为. 因为，所以，又，所以与“0是函数的唯一零点”矛盾.‎ 若，同理可得，在和之间存在的非0的零点，矛盾.‎ 因此，.于是，故，所以. ‎ ‎【模拟考场】‎ ‎1.已知,且,若,则的大小关系为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎2.【2015高考天津，理7】已知定义在 上的函数（为实数）为偶函数，记，则 的大小关系为( )‎ ‎（A） （B） （C） （D） ‎ ‎【解析】因为函数为偶函数，所以，即，‎ 所以 ‎,所以，故选C.‎ ‎【答案】C ‎3.【2015高考山东，文2】设则的大小关系是( )‎ A. B. C. D. ‎【解析】由在区间是单调减函数可知，，又，故选.‎ ‎【答案】C ‎ ‎【答案】C ‎6.【2015高考山东，理14】已知函数的定义域和值域都是 ，则 .‎ ‎【解析】若 ，则 在上为增函数,所以，此方程组无解；‎ 若 ，则在上为减函数,所以 ，解得 ，所以.‎ ‎【答案】 ‎ ‎7.【2014高考陕西版文第12题】已知，，则________.‎ ‎【解析】由得，所以，解得，故答案为.‎ ‎【答案】 ‎8.【2014，安徽文11】________．‎ ‎【答案】 ‎