2014年高考真题——数学理（新课标Ⅰ）原卷版 5页

2014 年普通高等学校招生全国统一考试（全国课标 1） 理科数学 注意事项： 1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答题前，考生务必将自己的姓 名、准考证号填写在答题卡上. 2.回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改 动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效. 3. 回答第Ⅱ卷时，将答案写在答题卡上，答在本试题上无效. 4. 考试结束，将本试题和答题卡一并交回. 第Ⅰ卷 一．选择题：共 12 小题，每小题 5 分，共 60 分。在每个小题给出的四个选项中，只有一项 是符合题目要求的一项。 1.已知集合 A={ x | 2 2 3 0xx   }，B={ x |－2≤ x ＜2＝，则 AB = A .[-2,-1] B .[-1,2） C .[-1,1] D .[1,2） 2. 3 2 (1 ) (1 ) i i   = A .1 i B .1 i C . 1 i D . 1 i 3.设函数 ()fx， ()gx的定义域都为 R，且 ()fx时奇函数， ()gx是偶函数，则下列结论正确 的是 A . ()fx ()gx是偶函数 B .| ()fx| ()gx是奇函数 C . ()fx| ()gx|是奇函数 D .| ()fx ()gx|是奇函数 4.已知 F 是双曲线C ： 223 ( 0)x my m m   的一个焦点，则点 F 到C 的一条渐近线的距离 为 A . 3 B .3 C . 3m D .3m 5.4 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益 活动的概率 A . 1 8 B . 3 8 C . 5 8 D . 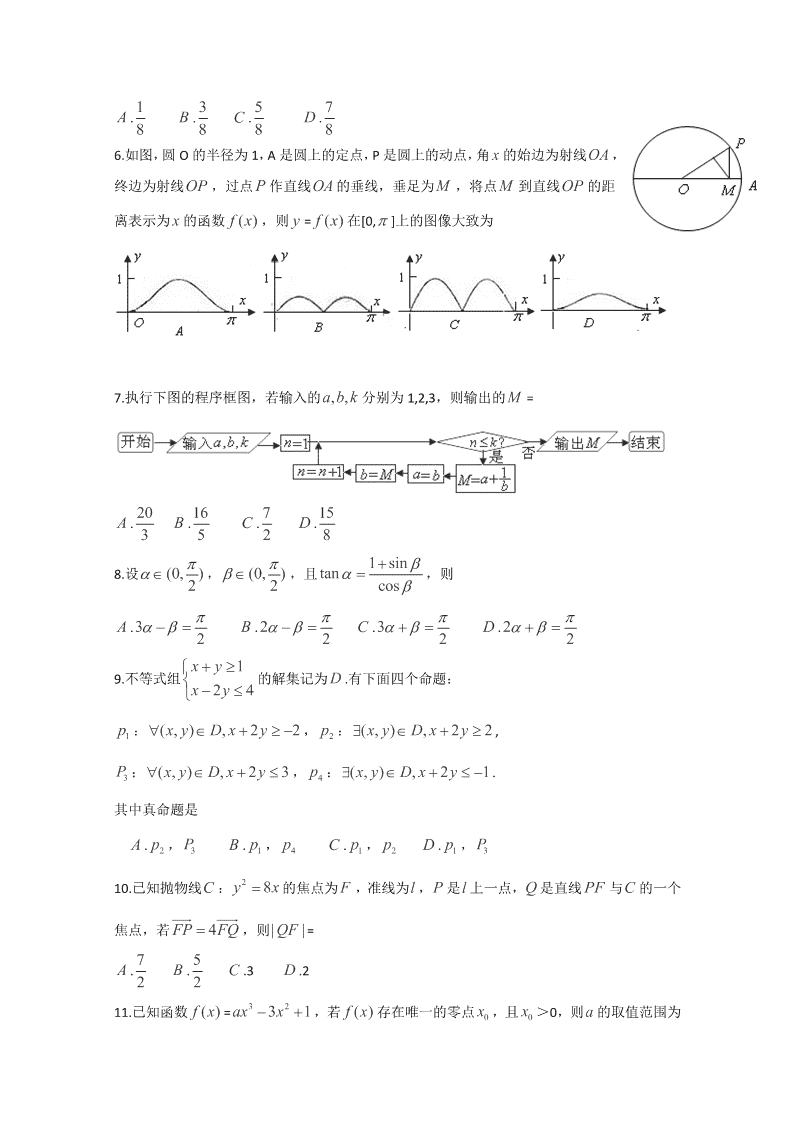7 8 6.如图，圆 O 的半径为 1，A 是圆上的定点，P 是圆上的动点，角 x 的始边为射线OA ， 终边为射线OP ，过点 P 作直线OA的垂线，垂足为 M ，将点 M 到直线OP 的距 离表示为 x 的函数 ()fx，则 y = ()fx在[0, ]上的图像大致为 7.执行下图的程序框图，若输入的 ,,a b k 分别为 1,2,3，则输出的 M = A . 20 3 B .16 5 C . 7 2 D .15 8 8.设 (0, )2   ， (0, )2   ，且 1 sintan cos    ，则 A .3 2  B . 2 2  C .3 2  D . 2 2  9.不等式组 1 24 xy xy    的解集记为 D .有下面四个命题： 1p ： ( , ) , 2 2x y D x y     ， 2p ： ( , ) , 2 2x y D x y    , 3P ： ( , ) , 2 3x y D x y    ， 4p ： ( , ) , 2 1x y D x y     . 其中真命题是 A . 2p ， 3P B . 1p ， 4p C . 1p ， 2p D . 1p ， 3P 10.已知抛物线C ： 2 8yx 的焦点为 F ，准线为l ，P 是l 上一点，Q 是直线 PF 与C 的一个 焦点，若 4FP FQ ，则||QF = A . 7 2 B . 5 2 C .3 D .2 11.已知函数 ()fx= 3231ax x，若 ()fx存在唯一的零点 0x ，且 0x ＞0，则 a 的取值范围为 A .（2，+∞） B .（-∞，-2） C .（1，+∞） D .（-∞，-1） 12.如图，网格纸上小正方形的边长为 1，粗实线画出的是某多面体的三视图，则该多面体的 个条棱中，最长的棱的长度为 A . 62 B . 42 C .6 D .4 第Ⅱ卷 本卷包括必考题和选考题两个部分。第（13）题-第（21）题为必考题，每个考生都必须作答。 第（22）题-第（24）题为选考题，考生根据要求作答。 二．填空题：本大题共四小题，每小题5分。 13. 8( )( )x y x y的展开式中 22xy的系数为 .(用数字填写答案) 14.甲、乙、丙三位同学被问到是否去过 A，B，C 三个城市时， 甲说：我去过的城市比乙多，但没去过 B 城市； 乙说：我没去过 C 城市； 丙说：我们三人去过同一个城市. 由此可判断乙去过的城市为 . 15.已知 A，B，C 是圆 O 上的三点，若 1 ()2AO AB AC，则 AB 与 AC 的夹角为 . 16.已知 ,,abc分别为 ABC 的三个内角 ,,A B C 的对边， a =2，且 (2 )(sin sin ) ( )sinb A B c b C    ，则 ABC 面积的最大值为 . 三.解答题：解答应写出文字说明，证明过程或演算步骤。 17.(本小题满分 12 分)已知数列{ na }的前 n 项和为 nS ， 1a =1， 0na  ， 1 1n n na a S ，其 中  为常数. (Ⅰ)证明： 2nnaa ； （Ⅱ）是否存在  ，使得{ na }为等差数列？并说明理由. 18. (本小题满分 12 分)从某企业的某种产品中抽取 500 件，测量这些产品的一项质量指标值， 由测量结果得如下频率分布直方图： (Ⅰ)求这 500 件产品质量指标值的样本平均数 x 和样本方差 2s （同一组数据用该区间的中点值 作代表）； （Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值 Z 服从正态分布 2( , )N  ，其中  近似为样本平均数 x ， 2 近似为样本方差 2s . （i）利用该正态分布，求 (187.8 212.2)PZ ； （ii）某用户从该企业购买了 100 件这种产品，记 X 表示这 100 件产品中质量指标值为于区间 （187.8,212.2）的产品件数，利用（i）的结果，求 EX . 附： 150 ≈12.2. 若 Z ～ 2( , )N  ，则 ()PZ       =0.6826， ( 2 2 )PZ       =0.9544. 19. (本小题满分 12 分)如图三棱锥 1 1 1ABC A B C 中，侧面 11BB C C 为菱形， 1AB B C . （Ⅰ）证明： 1AC AB ； （Ⅱ）若 1AC AB ， o 1 60CBB，AB=Bc， 求二面角 1 1 1A A B C的余弦值. 20. (本小题满分 12 分) 已知点 A（0，-2），椭圆 E ： 22 221( 0)xy abab    的离心率为 3 2 ， F 是椭圆的焦点，直线 AF 的斜率为 23 3 ，O 为坐标原点. (Ⅰ)求 E 的方程； （Ⅱ）设过点 A 的直线l 与 E 相交于 ,PQ两点，当 OPQ 的面积最大时，求l 的方程. 21. (本小题满分 12 分)设函数 1 ( 0 ln x x bef x ae x x  ，曲线 ()y f x 在点（1， (1)f 处的切 线为 ( 1) 2y e x   . (Ⅰ)求 ,ab； （Ⅱ）证明： ( ) 1fx . 请考生从第（22）、（ 23）、（ 24）三题中任选一题作答。注意：只能做所选定的题目。如果多 做，则按所做的第一个题目计分，作答时请用 2B 铅笔在答题卡上将所选题号后的 方框涂黑。 22.（本小题满分 10 分）选修 4—1：几何证明选讲 如图，四边形 ABCD 是⊙O 的内接四边形，AB 的延长线与 DC 的延 长线交于点 E，且 CB=CE .(Ⅰ)证明：∠D=∠E； （Ⅱ）设 AD 不是⊙O 的直径，AD 的中点为 M，且 MB=MC，证明： △ADE 为等边三角形. 23. （本小题满分 10 分）选修 4—4：坐标系与参数方程 已知曲线C ： 22 149 xy，直线l ： 2 22 xt yt    （t 为参数）. (Ⅰ)写出曲线C 的参数方程，直线l 的普通方程； （Ⅱ）过曲线C 上任一点 P 作与l 夹角为 o30 的直线，交l 于点 A ，求||PA 的最大值与最小 值. 24. （本小题满分 10 分）选修 4—5：不等式选讲 若 0, 0ab，且 11 abab . (Ⅰ) 求 33ab 的最小值； （Ⅱ）是否存在 ,ab，使得 2 3 6ab？并说明理由.