2019届中考数学一轮复习 第22课时 等腰三角形导学案（无答案） 4页

第22课时 等腰三角形 姓名 班级 ‎ 学习目标：‎ 掌握等腰三角形（等边三角形的）性质和判定，能灵活运用其轴对称性解决问题。‎ 学习重难点：‎ 灵活运用等腰三角形的轴对称性解决问题 学习过程：‎ 一、知识梳理 ‎1.相关概念：等腰三角形（腰、底、顶角、底角）、等边三角形（是等腰三角形的特例）．‎ ‎2.相关性质和判定：‎ ‎（1）等边对 ； 等角对 .‎ ‎（2）等腰三角形的顶角 、底边上的 、底边上的 相互重合.‎ ‎（3）等腰三角形是轴对称图形， （ 、 ）所在直线就是它的对称轴（等边三角形共有 条对称轴）.‎ ‎（4）等边三角形的三个内角都 ，并且每一个角都等于 . ‎ ‎（5）三个角都 的三角形是等边三角形；有一个角是 的 三角形是等边三角形.‎ ‎3.相关重要结论：等腰三角形两腰上的高、中线分别相等，两底角的平分线也相等；一腰上的高与底边的夹角是顶角的一半；顶角的外角平分线平行于这个三角形的底边.‎ 二、精典题例 例1、一个等腰三角形一边长为，另一边长为，那么这个等腰三角形的周长是(　)‎ ‎ ‎ 例2、等腰三角形一腰上的高与另一腰的夹角为，求该等腰三角形的底角的度数。‎ 4‎ 三、中考连接 四、反思总结 ‎1.本节课你复习了哪些内容？‎ ‎2.通过本节课的学习，你还有哪些困难？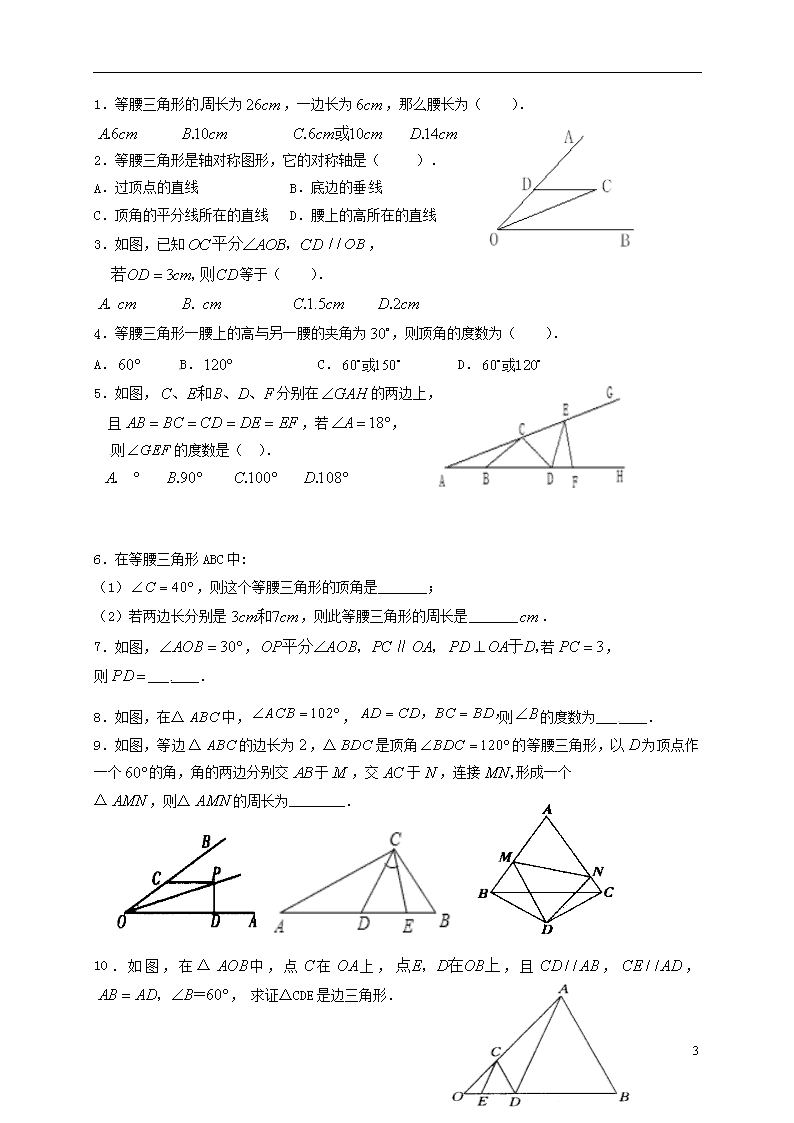‎ 五、课堂练习 4‎ ‎1．等腰三角形的周长为，一边长为，那么腰长为（ 　 ）．‎ ‎ ‎ ‎2．等腰三角形是轴对称图形，它的对称轴是（ ）．‎ A．过顶点的直线 B．底边的垂线 C．顶角的平分线所在的直线 D．腰上的高所在的直线 ‎3．如图，已知，‎ 等于（ 　 ）．‎ ‎ ‎ ‎4．等腰三角形一腰上的高与另一腰的夹角为，则顶角的度数为（ 　 ）．‎ A． B．　　 C． D．‎ ‎5．如图，分别在的两边上，‎ 且，若，‎ 则的度数是（ ）．‎ ‎ ‎ ‎6．在等腰三角形ABC中:‎ ‎（1），则这个等腰三角形的顶角是_______； ‎ ‎（2）若两边长分别是，则此等腰三角形的周长是_______．‎ ‎7．如图，，∥ 若，‎ 则_______．‎ ‎8．如图，在△中，，则的度数为_______．‎ ‎9．如图，等边△的边长为，△是顶角的等腰三角形，以为顶点作一个的角，角的两边分别交于，交于，连接形成一个 ‎△，则△的周长为________．‎ ‎　　　　　　　　　　　　　‎ ‎10．如图，在△中，点在上，，且，，，求证△CDE是边三角形．‎ 4‎ ‎11．如图，在△中，，，，那么△是等腰三角形吗？‎ ‎12．如图，在△中，，的垂直平分线分别与，交于.求证.‎ 4‎