- 304.80 KB
- 2021-06-02 发布
1
《圆》第一节 圆周角导学案 1
主编人: 主审人:
班级: 学号: 姓名:
学习目标:
【知识与技能】
理解圆周角的概念及其相关性质,并能运用相关性质解决有关问题
【过程与方法】
经历探索圆周角的有关性质的过程,体会分类、转化等数学思想方法,学会数学地思考问题
【情感、态度与价值观】
在探求新知的过程中学会合作、交流体会数学中的分类转化等方法。
【重点】
圆周角及圆周角定理
【难点】
圆周角定理的应用学习过程
一、自主学习
(一)复习巩固
1、 叫圆心角。
2、在同圆或等圆中,圆心角的度数等于它所对的 度数。
(二)自主探究
1、如图,点 A 在⊙O 外,点 B1 、B2 、B3 在⊙O 上,点 C 在⊙O 内,度量∠A、∠B1 、
∠B2 、∠B3 、∠C 的大小,你能发现什么?
∠B1 、∠B2 、∠B3有什么共同的特征?_________________。
归纳得出结论,顶点在_______,并且两边________________________的角叫做圆周角。
强调条件:①_______________________,②___________________________。
识别图形:判断下列各图中的角是否是圆周角?并说明理由.
2
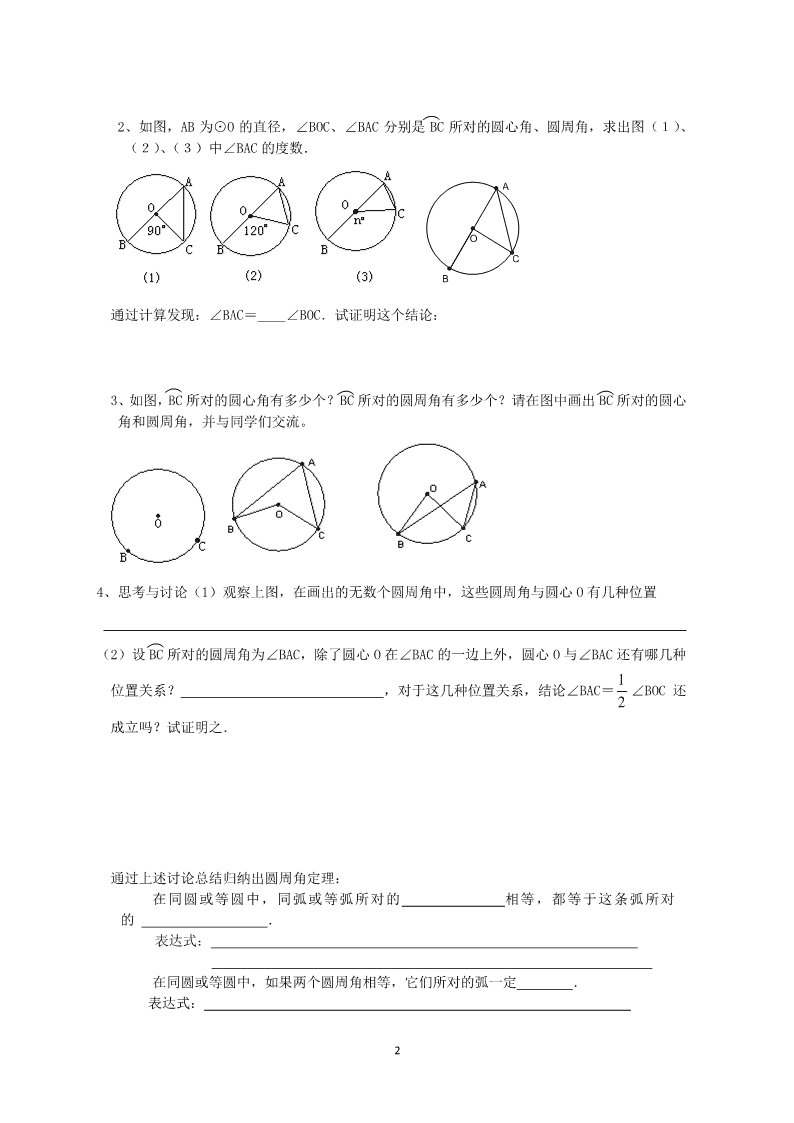
2、如图,AB 为⊙O 的直径,∠BOC、∠BAC 分别是 BC 所对的圆心角、圆周角,求出图(1)、
(2)、(3)中∠BAC 的度数.
O
C
B
A
通过计算发现:∠BAC=__∠BOC.试证明这个结论:
3、如图,BC 所对的圆心角有多少个?BC 所对的圆周角有多少个?请在图中画出 BC 所对的圆心
角和圆周角,并与同学们交流。
4、思考与讨论(1)观察上图,在画出的无数个圆周角中,这些圆周角与圆心 O 有几种位置
(2)设 BC 所对的圆周角为∠BAC,除了圆心 O 在∠BAC 的一边上外,圆心 O 与∠BAC 还有哪几种
位置关系? ,对于这几种位置关系,结论∠BAC=
2
1 ∠BOC 还
成立吗?试证明之.
通过上述讨论总结归纳出圆周角定理:
在同圆或等圆中,同弧或等弧所对的 相等,都等于这条弧所对
的 .
表达式:
在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定 .
表达式:
3
(三)、归纳总结:
1.圆周角与圆心角的相同点是 ,不同点是
2.一条弧所对的圆周角与圆心角有三种位置关系,即圆心角的顶点在圆周角的
“ ”,“ ”,“ ”;
(四)自我尝试:
1、如图,点 A、B、C、D 在⊙O 上,点 A 与点 D 在点 B、C 所在直线的同侧,∠BAC=350
(1)∠BDC=_______°,理由是_______________________.
(2)∠BOC=_______°,理由是_______________________.
O
A
B C
D
2、如图,点 A、B、C 在⊙O 上,
(1) 若∠BAC=60°,求∠BOC=______°;(2) 若∠AOB=90°,求∠ACB=______°.
3、如图,点 A、B、C 在⊙O 上,点 D 在圆外,CD、BD 分别交⊙O 于点 E、F,比较∠BAC 与
∠BDC 的大小,并说明理由。
二、教师点拔
圆周角的性质:①一条弧所对的圆周角等于该弧所对的圆心角的 。对于这一结论要
掌握同一条弧所对的圆周角与圆心角的三种位置关系,即圆心角的顶点在圆周角的
“ ”、“ ”、“ ”; ②在同一个圆中,同弧或等弧所对的圆周角 ,
都等于这条弧所对的圆心角的 ;在同圆或等圆中,相等的圆周角所对的弧相等。该
结论是证明 相等或 相等的常用方法:“由角找弧”“由弧找角”; ③半圆(或
直径)所对的圆周角是 ;90°的圆周角所对的弦是 ,这一结论:一是用来确
定圆心,二是为在圆中确定直角、构成垂直关系创造条件,并为在圆中证明直径提供了理
论依据。
三、课堂检测
1、如图,点 A、B、C 在⊙O 上,点 D 在⊙O 内,点 A 与点 D 在点 B、C 所在直线的同侧,
比较∠BAC 与∠BDC 的大小,并说明理由.
4
2、如图,AC 是⊙O 的直径,BD 是⊙O 的弦,EC∥AB,交⊙O 于 E。图中哪些与
2
1 ∠BOC 相等?
请分别把它们表示出来.
3、如图,在⊙O 中,弦 AB、CD 相交于点 E,∠BAC=40°,∠AED=75°,求∠ABD 的度数.
四、课外训练
1、如图,△ABC 的 3 个顶点都在⊙O 上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
2、如图,点 A、B、C、D 在同一个圆上,四边形 ABCD 的对角线把 4 个内角分成 8 个角,
在这 8 个角中,有几对相等的角?请把它们分别表示
3、如图,AB 是⊙O 的直径,∠BOC=120°,CD⊥AB,则∠ABD=___________。
4、如图,△ABC 的 3 个顶点都在⊙O 上,∠BAC 的平分线交 BC 于点 D,交⊙O 于点 E,则图中
相等的圆周角有______________________ 。
5、如图,点 A、B、C、D 在⊙O 上,∠ADC=∠BDC=60°.判断△ABC 的形状,并说明理由.
相关文档
- 高考数学圆锥曲线形成性测试卷文科2021-06-02 16:22:2826页
- 2020高中物理 第二章 匀速圆周运动2021-06-02 16:16:554页
- 2019年高考数学总复习检测第63讲 2021-06-02 16:03:563页
- 高中数学必修2教案:圆与圆的位置关2021-06-02 15:49:283页
- 人教版必修二5.7《生活中的圆周运2021-06-02 15:20:314页
- 专题16 圆锥曲线的综合问题-2017年2021-06-02 15:11:5523页
- 新北师大版六年级数学上册同步练习2021-06-02 15:10:282页
- 六年级上册数学教案-5 圆的认识 ︳青2021-06-02 14:43:0214页
- 2020九年级数学下册 第2章 直线与2021-06-02 14:31:095页
- 六年级上册数学教案-5圆的周长 ︳青2021-06-02 13:54:034页