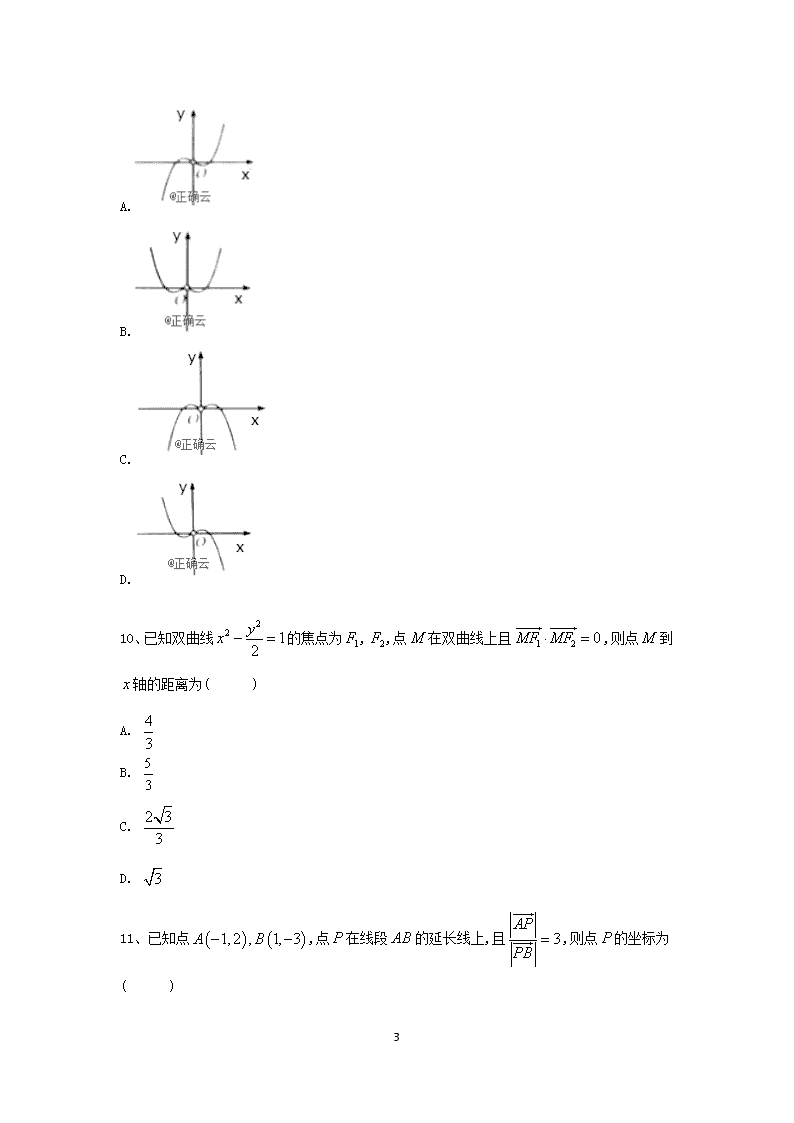2020高考全国卷数学（理）模拟卷（五） 17页

‎2020高考全国卷数学（理）模拟卷（五）‎ ‎1、已知集合,,则∁ (   )‎ A. B. C. D. ‎ ‎2、已知复数 (为虚数单位),则的共轭复数(   )‎ A. B. C. D. ‎ ‎3、已知直线平面,直线平面,则“”是“”的(   )‎ A.充分不必要条件                  B.必要不充分条件 C.充要条件                     D.既不充分也不必要条件 ‎4、已知等差数列中,若,则数列前9项的和为(   )‎ A.297        B.144        C.99         D.66‎ ‎5、将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到同一个班,则不同分法的种数为(   )‎ A.18         B.24         C.30         D.36‎ ‎6、直线与圆的位置关系是(   )‎ 17‎ A.相离     B.相切 C.相交     D.根据的值确定 ‎7、已知函数是定义在区间上的偶函数,当时, 是减函数,如果不等式成立,则实数的取值范围(   )‎ A. B. C. D. ‎ ‎8、三棱锥的三视图如图所示,则该三棱锥外接球的体积为(   )‎ A. B. C. D. ‎ ‎9、函数的图象大致为(   )‎ 17‎ A. B. C. D.‎ ‎10、已知双曲线的焦点为,,点在双曲线上且,则点到轴的距离为(   )‎ A. B. C. D. ‎ ‎11、已知点,点在线段的延长线上,且,则点的坐标为(   )‎ 17‎ A. B. C. D. ‎ ‎12、设是半径为的球面上的四个不同点,且满足,,,用、、分别表示、、的面积,则的最大值是(   )‎ A. B.2 C.4 D.8‎ ‎13、函数的零点的个数是__________‎ ‎14、已知 满足约束条件则目标函数的最小值为___________.‎ ‎15、已知抛物线的焦点为,准线与轴的交点为 ,点在抛物线上,且,则的面积为__________‎ ‎16、如左图是第七届国际数学教育大会(简称)的会徽图案,会徽的主体图案是由右图的一连串直角三角形演化而成的,其中 17‎ ‎ 如果把右图中的直角三角形继续作下去.记的长度构成数列,则此数列的通项公式为__________.‎ ‎17、已知向量,设.‎ ‎1.求函数的解析式及单调递增区间; 2.在中, 分别为内角的对边,且,求的面积.‎ ‎18、如图,已知正方形和矩形所在的平面互相垂直, 是线段的中点.‎ ‎1.求二面角的大小.‎ ‎2.试在线段上确定一点,使与所成的角是.    ‎ ‎19、椭圆的左右焦点分别为,与轴正半轴交于点,若为等腰直角三角形,且直线被圆所截得的弦长为2.‎ ‎1.求椭圆的方程;‎ 17‎ ‎2.直线与椭圆交于点,线段的中点为,射线与椭圆交于点,点为重心,探求面积是否为定值,若是求出这个值,若不是求的取值范围 ‎20、—个口袋中装有大小相同的个红球 且和5个白球,每次从中任取两个球,当两个球的颜色不同时,则规定为中奖.‎ ‎1.试用表示一次取球中奖的概率;‎ ‎2.记从口袋中三次取球(每次取球后全部放回)恰有一次中奖的概率为,求的最大值.‎ ‎21、设函数.‎ ‎1.求函数的单调区间;‎ ‎2.记函数的最小值为,证明: .‎ ‎22、已知曲线的极坐标方程是,直线的参数方程是 (为参数).‎ ‎1.将曲线的极坐标方程化为直角坐标方程;‎ ‎2.设直线与轴的交点是是曲线上一动点,求的最大值.‎ ‎23、[选修4-5:不等式选讲]‎ 已知函数 ‎1.当时,解不等式 ‎2.求函数的最小值 ‎ ‎ ‎ ‎ 17‎ ‎ ‎ 答案以及解析 ‎1答案及解析：‎ 答案：C 解析：,故选C ‎ ‎ ‎2答案及解析：‎ 答案：C 解析：利用复数的除法运算,化简复数,从而得到的共轭复数.‎ ‎ ‎ ‎3答案及解析：‎ 答案：A 解析：根据已知题意,由于直线平面,直线平面,如果两个平面平行,则必然能满足,但是反之,如果,则对于平面可能是相交的,故条件能推出结论,但是结论不能推出条件,故选A 考点:本试题主要是考查了立体几何中点线面的位置关系运用。‎ 点评:解决该试题的关键是利用面面平行的性质定理和线面平行、垂直的性质定理来熟练的判定其位置关系,同时结合了充分条件的概念,来判定命题的条件和结论之间的关系运用,属于基础题。‎ ‎ ‎ ‎4答案及解析：‎ 答案：C 17‎ 解析：由,得.‎ 由,‎ 得.‎ 所以 ‎ ‎ ‎5答案及解析：‎ 答案：C 解析：‎ ‎ ‎ ‎6答案及解析：‎ 答案：D 解析：因为圆心坐标为,所以圆心到直线的距离为,‎ 所以与圆的半径的大小关系根据的值确定,‎ 故选D.‎ ‎ ‎ ‎7答案及解析：‎ 答案：A 解析：‎ ‎ ‎ ‎8答案及解析：‎ 17‎ 答案：A 解析：三棱锥的直观图如图,设H为三棱锥外接球的球心, 为外接圆的圆心, 为外接圆的圆心.取AC的中点O,连接,易知,‎ ‎∵平面平面,平面, 平面, 平面,‎ ‎∵平面, ∴,连接,易知,‎ ‎∴四边形为平行四边形,∴.‎ 在中, ,‎ 即三棱锥外接球的半径为,故所求体积为.‎ ‎ ‎ ‎9答案及解析：‎ 答案：B 解析：‎ ‎ ‎ ‎10答案及解析：‎ 答案：C 17‎ 解析：‎ 设,‎ 由条件知道,‎ ‎∴,①‎ ‎.②‎ 由①②,得.‎ 设所求距离为,则,∴.‎ ‎ ‎ ‎11答案及解析：‎ 答案：C 解析：‎ ‎ ‎ ‎12答案及解析：‎ 答案：B 解析：设均大于),由已知得两两垂直,所以可将四面体补形为长方体.该长方体的体对角线为球的直径,所以,所以当且仅当时取等号,则的最大值为,故选B.‎ ‎ ‎ ‎13答案及解析：‎ 17‎ 答案：1‎ 解析：‎ ‎ ‎ ‎14答案及解析：‎ 答案：‎ 解析：‎ ‎ ‎ ‎15答案及解析：‎ 答案：8‎ 解析：‎ ‎ ‎ ‎16答案及解析：‎ 答案：‎ 解析：‎ ‎ ‎ ‎17答案及解析：‎ 答案：1.向量,‎ 令: ,‎ 解得: ,‎ 17‎ 故函数的单调递增区间为: 2.在中, 分别为内角的对边, ,‎ 则: ,‎ 解得: ‎ 利用余弦定理: ,且.‎ 解得: ‎ 所以的面积为: ‎ 解析：‎ ‎ ‎ ‎18答案及解析：‎ 答案：1.以为正交基底,建立空间直角坐标系,则,.‎ 面的法向量,‎ 设面法向量,则,‎ 所以,令,得,所以.‎ 设二面角的大小为.‎ 17‎ 从而,∴,‎ 故二面角的大小为. 2.依题意得,设,则.‎ 因为,所以,解得,‎ 所以点应在线段的中点处.‎ 解析：‎ ‎ ‎ ‎19答案及解析：‎ 答案：1.由为等腰直角三角形可得,直线被圆所截得的弦长为2,所以,所以椭圆的方程为 2.若直线的斜率不存在,则 若直线的斜率存在,设直线l的方程为,‎ 设,‎ 则,‎ 由题意点为重心,设,‎ 则,‎ 所以,‎ 17‎ 代入椭圆得, ‎ 设坐标原点到直线l的距离为,则的面积 综上可得面积为定值 ‎ 解析：‎ ‎ ‎ ‎20答案及解析：‎ 答案：1.每次从个球中任取两个,有种取法, 其中两个球的颜色不同的取法有种,一次取球中奖的概率为. 2.设每次取球中奖的概率为,三次取球中恰有一次中奖的概率是,对的导数.‎ 因而在上为增函数, 在上为减函数.‎ ‎∴当时, .‎ 17‎ 解析：‎ ‎ ‎ ‎21答案及解析：‎ 答案：1.显然的定义域为.‎ ‎.‎ ‎∵,‎ ‎∴若,此时,在上单调递减;‎ 若,此时,在上单调递增;‎ 综上所述: 在上单调递减,在上单调递增. 2.由2知: ,即: .‎ 要证,即证明,即证明,‎ 令,则只需证明,‎ ‎∵,且,‎ ‎∴当,,此时,在上单调递减;‎ 当,,此时,在上单调递增,‎ ‎∴.‎ ‎∴.  ∴.‎ 解析：‎ ‎ ‎ 17‎ ‎22答案及解析：‎ 答案：1.曲线的极坐标方程可化为 ……………‎ 又,‎ ‎[所以曲线的直角坐标方程为…… 2.将直线l的参数方程化为直角坐标方程,得………………‎ 令,得,即点的坐标为(2,0).‎ 又曲线为圆,圆的圆心坐标为(1,0),半径,则… …………       ‎ 所以………………………………‎ 解析：‎ ‎ ‎ ‎23答案及解析：‎ 答案：1.∵,‎ ‎∴原不等式为    ‎ 或或,‎ 或 ‎∴原不等式的解集为 2. 由题意得 ‎ ‎, ‎ 17‎ 当且仅当,即,且时, 取最小值 解析：‎ ‎ ‎ 17‎