2018届二轮复习　天体运动问题课件（共19张）（全国通用） 19页

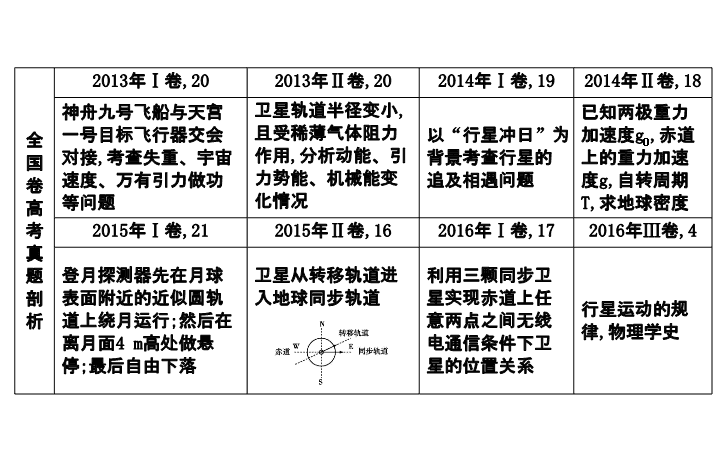
高考热点剖析　天体运动问题 全国卷高考真题剖析 2013 年 Ⅰ 卷 ,20 2013 年 Ⅱ 卷 ,20 2014 年 Ⅰ 卷 ,19 2014 年 Ⅱ 卷 ,18 神舟九号飞船与天宫一号目标飞行器交会对接 , 考查失重、宇宙速度、万有引力做功等问题 卫星轨道半径变小 , 且受稀薄气体阻力作用 , 分析动能、引力势能、机械能变化情况 以“行星冲日”为背景考查行星的追及相遇问题 已知两极重力加速度 g 0 , 赤道上的重力加速度 g, 自转周期 T, 求地球密度 2015 年 Ⅰ 卷 ,21 2015 年 Ⅱ 卷 ,16 2016 年 Ⅰ 卷 ,17 2016 年 Ⅲ 卷 ,4 登月探测器先在月球表面附近的近似圆轨道上绕月运行 ; 然后在离月面 4 m 高处做悬 停 ; 最后自由下落 卫星从转移轨道进入地球同步轨道 利用三颗同步卫星实现赤道上任意两点之间无线电通信条件下卫星的位置关系 行星运动的规律 , 物理学史 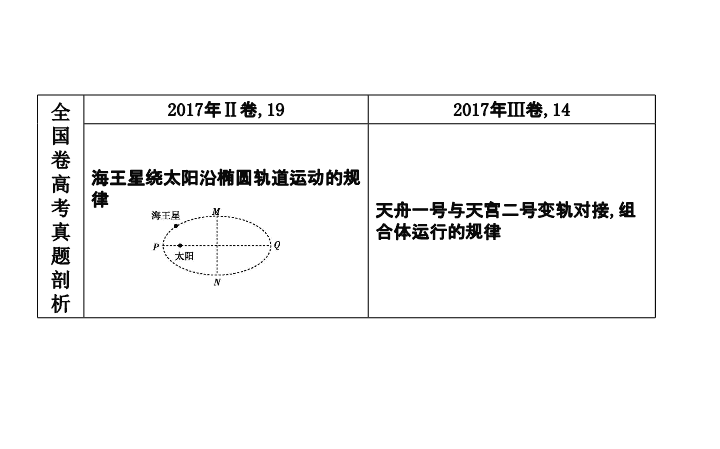全国卷高考真题剖析 2017 年 Ⅱ 卷 ,19 2017 年 Ⅲ 卷 ,14 海王星绕太阳沿椭圆轨道运动的规律 天舟一号与天宫二号变轨对接 , 组合体运行的规律 技 法 提 炼 1. 牢记两个基本思路 : 天体运动的向心力由万有引力提供 ; 不考虑星球自转 , 星球表面上物体的重力等于万有引力 . 2. 变轨规律 : (1) 加速会离心 , 轨道半径变大 ; 减速会向心 , 轨道半径变小 . (2) 轨道升高机械能增加 , 轨道降低机械能减少 , 同一轨道上稳定运行过程中机械能守恒 . 3. 天体运行时线速度、角速度、周期与半径的关系口诀 : 高轨道低转速长 周期 . 4. 牢记同步卫星的两个特点 : (1) 同步卫星绕地心做匀速圆周运动的周期等于地球的自转周期 ; (2) 所有同步卫星都在赤道上空相同的高度上 . 常 考 类 型 1. 万有引力与重力的关系及向心力公式的应用 ; 2. 万有引力定律结合几何关系的应用 ; 3. 卫星在定轨运行时 , 不同轨道卫星各个物理量的比较和计算 ; 4. 卫星的变轨问题 : 发射中的变轨问题 , 对接中的轨道控制 , 变轨前后各物理量的比较 . 【 热点集训 】 1.[ 卫星的变轨与对接 ]( 2016 · 北京卷 ,18 ) 如图所示 , 一颗人造卫星原来在椭圆轨道 1 绕地球 E 运行 , 在 P 点变轨后进入轨道 2 做匀速圆周运动 . 下列说法正确的是 ( 　 　 ) A. 不论在轨道 1 还是在轨道 2 运行 , 卫星在 P 点的速度都相同 B. 不论在轨道 1 还是在轨道 2 运行 , 卫星在 P 点的加速度都相同 C. 卫星在轨道 1 的任何位置都具有相同加速度 D. 卫星在轨道 2 的任何位置都具有相同动量 B 解析 : 卫星在轨道 1 运行到 P 点时需要加速才能进入轨道 2 运行 , 因此卫星在两轨道的 P 点时速度不同 , 但所受力相同 , 加速度相同 ; 卫星在轨道 1 运行时在不同位置所受万有引力大小、方向均不同 , 则加速度也不同 ; 卫星在轨道 2 做匀速圆周运动 , 在不同位置速度方向不同 , 因此动量不同 , 只有选项 B 正确 . 2.[ 卫星运行参量的分析 ]( 2017 · 湖北荆州模拟 ) 火星和地球绕太阳运行的轨道可近似视为圆形 , 若已知火星和地球绕太阳运行的周期之比 , 则由此可求得 ( 　 　 ) A. 火星和地球受到太阳的万有引力之比 B. 火星和地球绕太阳运行速度大小之比 C. 火星和地球表面的重力加速度之比 D. 火星和地球的第一宇宙速度之比 B 3.[ 万有引力定律结合几何关系的应用 ]2014 年 12 月 7 日 , 中国和巴西联合研制的地球资源卫星 “ 04 星 ” 在太原成功发射升空 , 进入预定轨道 , 已知 “ 04 星 ” 绕地球做匀速圆周运动的周期为 T, 地球相对 “ 04 星 ” 的张角为 θ, 引力常量为 G, 则地球的密度为 ( 　 　 ) B 4. [ 卫星的变轨与对接 ]( 2017 · 湖北黄冈质检 ) 卫星发射进入预定轨道往往需要进行多次轨道调整 . 如图所示 , 某次发射任务中先将卫星送至近地轨道 , 然后再控制卫星进入椭圆轨道 . 图中 O 点为地心 ,A 点是近地轨道和椭圆轨道的交点 , 远地点 B 离地面高度为 6R(R 为地球半径 ). 设卫星在近地轨道运动的周期为 T, 下列对卫星在椭圆轨道上运动的分析 , 正确的是 ( 　 　 ) A. 控制卫星从图中低轨道进入椭圆轨道需要使卫星减速 B. 卫星通过 A 点时的速度是通过 B 点时速度的 6 倍 C. 卫星通过 A 点时的加速度是通过 B 点时加速度的 6 倍 D. 卫星从 A 点经 4T 的时间刚好能到达 B 点 D 5.[ 万有引力与重力的关系 ] 假设火星可视为质量均匀分布的球体 , 已知 “ 火卫一 ” ( 火星的卫星 ) 绕火星做圆周运动的半径为 R, 周期为 T, 火星的半径为 R 0 , 自转周期为 T 0 , 则火星表面的重力加速度在赤道处与两极处大小的比值为 ( 　 　 ) D 6.[ 天体质量和密度的估算 ]( 2017 · 江苏泰兴模拟 ) 我国成功地进行了 “ 嫦娥三号 ” 的发射和落月任务 , 进一步获取月球的相关数据 . 该卫星在月球上空绕月球做匀速圆周运动时 , 经过时间 t, 卫星行程为 s, 卫星与月球中心连线扫过的角度是 θ 弧度 , 引力常量为 G, 月球半径为 R, 则可推知月球密度的表达式是 ( 　 　 ) C 7. [ 卫星追及问题 ] 如图所示 , 有 A,B 两颗卫星绕地心 O 做圆周运动 , 旋转方向相同 .A 卫星的周期为 T 1 ,B 卫星的周期为 T 2 , 在某一时刻两卫星相距最近 , 则 ( 引力常量为 G)( 　 　 ) A. 两卫星经过时间 t=T 1 +T 2 再次相距最近 C. 若已知两颗卫星相距最近时的距离 , 可求出地球的质量 D. 若已知两颗卫星相距最近时的距离 , 可求出地球表面的重力加速度 C 谢谢观赏！